
東京大学2020文科 数学 大問4 整式+数列的発想
お世話になります。ドリームラーナーズの石原です。鳥取県倉吉市で進路指導と学習法指導の塾を運営しています。学習指導は中学生・高校生・大人、英語の指導は小学生から対応しています。LINEなどを活用して、遠隔地でも進路指導・学習指導に対応しています。
今日は過去問解説にチャレンジします。東京大学文科の数学です。問題本体は載せませんので、ご自分で用意してください。
なるべく「与えられた問題文をどう読むか、読んで何を考えるか」と言う点を重点的に解説していきたいと思います。あと、「いかに簡単に、楽して解くか」も重視します。数式を試行錯誤してぐちゃぐちゃやって解けた、と言う話はあまり参考にならないと思いますし、時間内に解ききれません。載せているのは考え方だけです。私が普段やっている指導では、これを小出しにしながら誘導していくスタイルを取っています。
大問4:状況整理
ひと目見て、よくわからない問題、ちゃんと全貌を見てみたり、とりあえずnに1とか2とか入れてみてどんな式になるかとか予想するなどしてみましょう。とりあえず(1)を解いてみても良いんですが、(2)は数列aを規則的に扱う素材だと思いますので、そちらを少し考察してからの方が上手いやり方が考えつきそうなので、ちょっと飛ばして(2)の考察を行います。
大問4(2)の考察
nが小さいうちは計算できるので、とりあえずn=1,2,3あたりで、式を作ってみます。
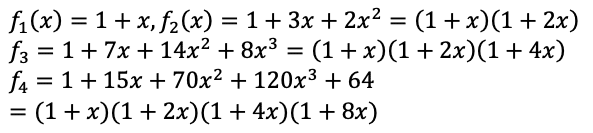
となるので、
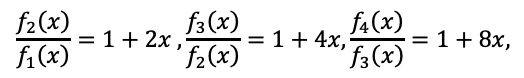
こうなります。ここから、予想として、
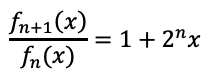
これが閃きます。で、これが成り立つには、この式で
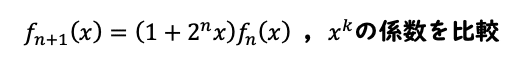
をやってみると、
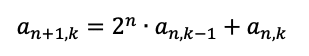
こうなって欲しいのですが、これをこう解釈すると、成立することがわかります。〜の和、は省略しています。

ただし、k=n+1のときと、k=1のときだけ、次のようになります。
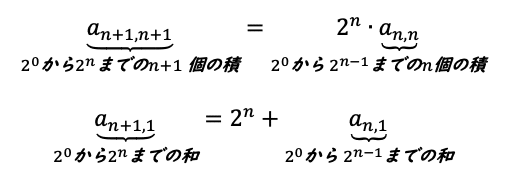
ではまず、これを使って、(1)を解いて、(2)の説明に入っていきます。
大問4(1):数列で解く
導入として、上で説明した

及び
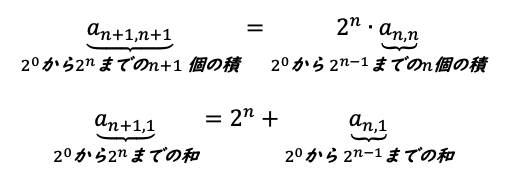
を示してから、a_n,2について同様の式を立てます。a_n-1,1は計算できるのでしてしまいます。
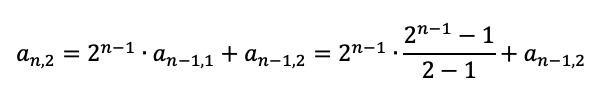
で、これをこのように変形すると階差数列になるとわかります。
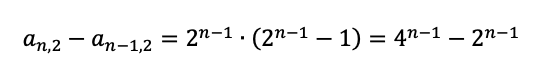
ということで階差数列で求めます。初項の位置(k=2)に注意しましょう。
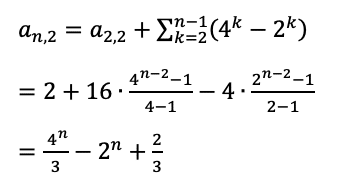
となります。この式で、階差を作れないn=2のときも成立します。
別解として(2^0+2^1+2^2+...+2^(n-1))^2を使って計算することもできます。
大問4(2):予想して、攻める
前半は、考察で示した

および
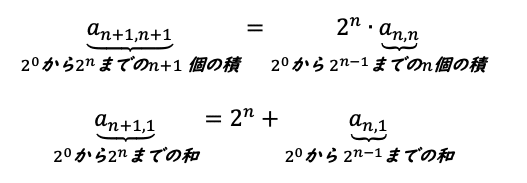
を活用します。f_n+1(x)を記述します。

(ここから、n+1 -> nに降ろしていきます。)
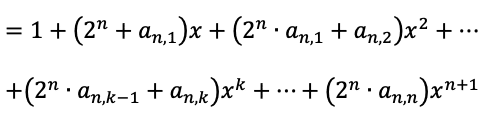
(これを、f_n(x)が出てくるように式変形します。)
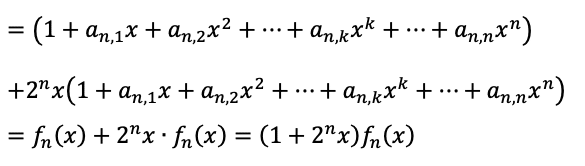
以上より、
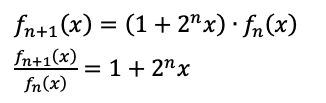
と表せます。
次ですが、まず最初に求めた式を使ってf_n(x)を一般化して表します。
というのも、これも実験してみると、予想として
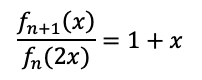
が出てくるのです。(1+x)って、前半で求めた(1+2^n x)のn=1のときですよね。何か関係があるのではないかと思いますが、今手元にある材料ではこいつらしかないので(もう問題も中盤なので)、掘り下げていきたいと思います。
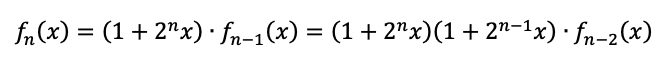
これを繰り返し適用していくのですが、
![]()
に注意して、
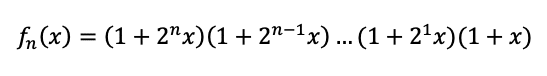
こうなります。で、f(2x)は
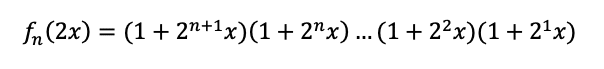
こうです。あれ?これって
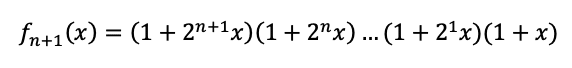
と似てますよね。比べると、後ろに(1+x)がない。ということで、
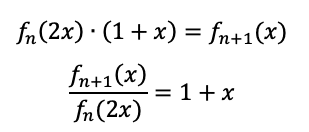
示せました。
大問4(3):(2)が出せれば問題なく出せる
まず、要求されている式が導出できそうな、一番近い形のものを今まで使っていなかったチェックしてみると、

これですかね。ただ、これを用いて導出したのは
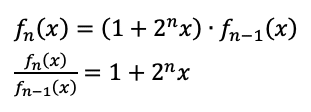
これでした。ということは、先ほど導出した
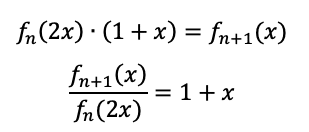
こっちの方からは何か関係式が出せないかな?と思って、x^kの係数比較をやってみると…
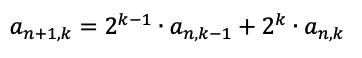
これが出てきました。2つの式それぞれ、kをk+1にして、要求されているものに近い形にしましょう。2つの式を並べてみると、
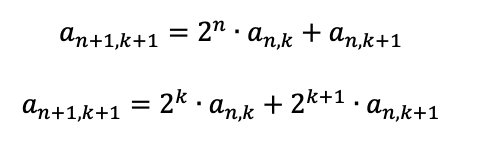
これらを連立方程式として、a_n,k+1を消去して、求められそうですね。
上の方程式に2^k+1をかけて、
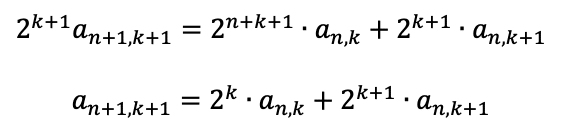
辺辺引くと、
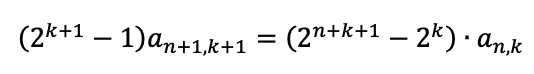
よって、
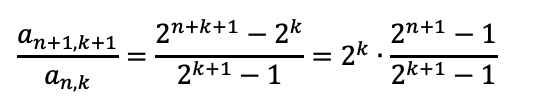
となりました。
難易度は例年並みでしょうね。東大文系数学は読んでわからせようとする良問が多くて好きです。
本日は以上です。
難関大志望者の中で勝ち残る学習法を公式ウェブサイトで公開中!
LINEやSkypeによる無料相談も受付中!
いいなと思ったら応援しよう!

