
京都大学2020 文系数学 大問3 整数
お世話になります。ドリームラーナーズの石原です。鳥取県倉吉市で進路指導と学習法指導の塾を運営しています。学習指導は中学生・高校生・大人、英語の指導は小学生から対応しています。LINEなどを活用して、遠隔地でも進路指導・学習指導に対応しています。
今日は過去問解説にチャレンジします。京都大学の文系数学の大問3です。問題本体は載せませんので、ご自分で用意してください。
なるべく「与えられた問題文をどう読むか、読んで何を考えるか」と言う点を重点的に解説していきたいと思います。あと、「いかに簡単に、楽して解くか」も重視します。数式を試行錯誤してぐちゃぐちゃやって解けた、と言う話はあまり参考にならないと思いますし、時間内に解ききれません。載せているのは考え方だけです。私が普段やっている指導では、これを小出しにしながら誘導していくスタイルを取っています。
大問3:問題を観察する
アプローチは当該年度2020年の理系の整数問題と同じです。つまり、2で4回割れるようなものを考えていけばよいのです。16をいきなり考えるのは骨が折れます。
大問3:2で割っていく
では早速やっていきましょう。aは「奇数」、m,nは整数として、以下の関数が16で割り切れるようなm,nが存在するaの条件を求めていきます。
![]()
こうですから、まずはmとnが2で割り切れるかどうかから確認していきましょう。以下全て、2を法として合同式を進めていきます。
m,nの偶奇で、fの偶奇がどう変わるのか調べてみると、以下のようになります。
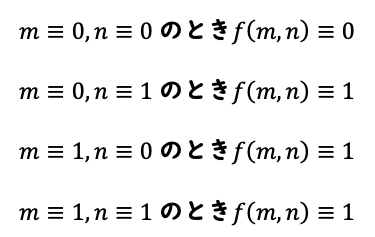
まずmとnはそもそも偶数でなければ16で割ることすらできないのがわかります。では具体的な数値を入れてみると、
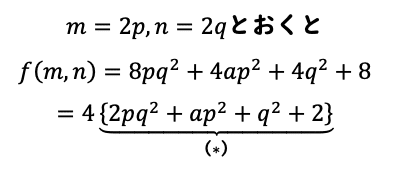
となります。4で括れているので、中身(*)について見ていくと、pやqの値によって2で割れるかどうか確認できそうです。
計算過程は省略しますが、これもp,qの偶奇で調べると、以下のように判明します。
![]()
では片方ずつやっていきましょう。
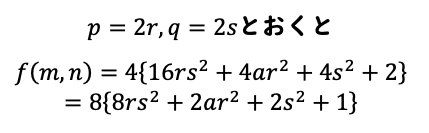
こちらだと、8で括れはしましたが、中身がどうしても奇数になってしまいます。これでは16で割り切れることはかないません。
ではもう片方を

ということで、やっと16で割り切れそうなところまで辿り着きました。
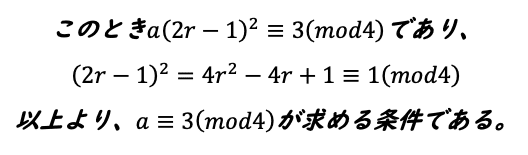
本日は以上です。
16で割れるかどうかをいきなり評価するのではなく、2ずつ割れるか考えていって限定していくことが、解答を展開していく上では重要だといえます。これは理系の整数問題でも同じでした。
難関大志望者の中で勝ち残る学習法を公式ウェブサイトで公開中!
LINEやSkypeによる無料相談も受付中!
いいなと思ったら応援しよう!

