
数学が苦手でも大丈夫!自然数の和と累乗の和を楽しむための入門ガイド
1 はじめに
みなさんに質問です!
(1) $${1+2+3+4+…+100=}$$
(2) $${1^2+2^2+3^2+4^2+…+100^2=}$$
$${1^2=1×1, 2^2=2×2}$$のことです。
この2問、普通に足し算するのは骨が折れますよね?
この記事では、こういう$${1^○+2^○+…}$$のような計算を手早くするために数学者たちが考えてきた画期的な方法を紹介します!
ぜひ最後まで読んでいただければ嬉しいです😆
2 1+2+3+4+…+100=?
実はこの計算、数学者ガウスが9歳の頃、小学校の算数の先生に出題されて即答したという逸話があります。
ではどのように工夫して計算したのかというと$${\textcolor{#228B22}{順番を入れ替えて足し合わせる}}$$という方法です!
$${1+2+3+4+…+100=}$$を
$${100+99+98+97+…+1=}$$のように足す順番を入れ替えたものを用意して、それぞれの1番目の数同士(1と100)、2番目の数同士(2と99)、3番目の数同士(3と98)…100番目の数同士(100と1)を足します。そうすると、全て101になりますよね?
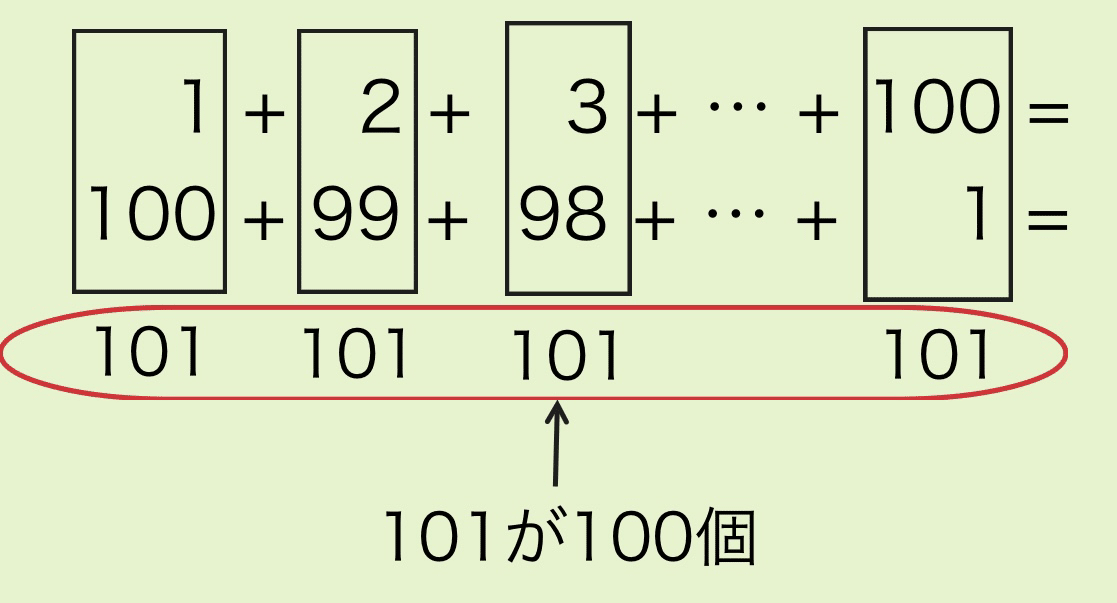
つまり101が100個出来たことになります。
$${101×100=10100}$$なので、答えは「10100」としたいところですが、だめですね!だって10100 は、$${1+2+3+4+…+100=}$$を2回足した答えだから、2で割る必要があります。
よって答えは「5050」となります。$${1+2+3+4+…+100=5050}$$
公式にすると、
$${1+2+3+…+n=\frac{1}{2}×n(n+1)}$$
※今回は$${n}$$が100の場合です。
ちなみに、なぜ足す順番を入れ替えたものを用意して、それぞれの1番目の数同士(1と100)のように足し合わすと全部101になるのかというと、数列$${{a_n}={1,2,3,…,n}}$$が等差数列という特殊な数列だからです。
等差数列については、また別の記事で書きたいと思います。
3 1^2+2^2+3^2+…100^2=
さて、次は$${1^2+2^2+3^2+4^2+…+100^2=}$$です。
これを計算するには、まず次のような数字の書かれた三角形のカードを用意します。

このカードに書かれている数学を全部足せば、$${1^2+2^2+3^2+4^2+…+100^2=}$$の答えが出ますね。

ではどのようにに工夫して計算するかというと、下の図のようにこの三角形のカードを60°、120°回転したカードを1枚ずつ用意します。

次に、元のカードと回転させた2枚のカードを重ねます。そして、回転させて重なった3つの数字を足します。例えば、図の○で囲んでいるところは、1と100と100が重なっているから$${1+100+100}$$になります。重なった3つの数字を足すと、どの箇所も201です。

あとは、この201がいくつあるかを考えれはいいので、元のカードで見ると、1は1個、2は2個3は3個、100は100個あるのだから、
$${1^2+2^2+3^2+4^2+…+100^2}$$
$${=\frac{1}{3}×(1+100+100)×(1+2+3+…+100)}$$
$${1+2+3+…+100=5050}$$だから、
$${1^2+2^2+3^2+…100^2}$$
$${=\frac{1}{3}×201×5050}$$
$${= 338,350}$$
となります。
これを公式にすると、
$${1^2+2^2+3^2+…+100^2}$$
$${=\frac{1}{3}×(1+n+n)×\frac{1}{2}n(n+1)}$$
$${=\frac{1}{6}n(n+1)(2n+1)}$$
※今回は$${n}$$が100の場合です。
この三角形のカードを作って考えるという発想はすごいですね!
4 自然数の3乗の和について
ここまで読んでいただいた方なら、
$${1^3+2^3+3^3+…+100^3=}$$
は、どう考えればいいのか気になりますよね?気になると言ってください笑
これ、さっきのような三角形のカードを作る、のような工夫が思いつかないんです!
でも3乗なので、立体を上手く使えばできるはずです!もしわかった方がいらっしゃれば教えてください!
5 自然数の4乗以上の和について
$${1^4+2^4+3^4+…+100^4=}$$
は、上手く図形を使って求められるかというとNOです。なぜなら、私たちは3次元、つまり立体までしか表現できないからです!
じゃあどうするかというと、式変形を上手く使って考えます!
これについては、また次回書きます!
6 おわりに
高校では、この自然数の累乗の和について、公式を覚えて終了としていたのが私でした。
しかし、自主的に色んな参考書を使って調べていくと教科書にはないアプローチで公式を作る方法を載せているのがあったりして楽しいです!
もちろん入試を受ける場合は公式を覚えた方がいいと思いますが、その背景を知ると、ド忘れした時に自分で公式を導くことだってできます!
また、先人たちの工夫に触れることで、新しいインスピレーションが生まれることだってあると思います!
公式を覚えるだけだともったいない!!
最後まで読んでいただき、ありがとうございました!!
