
雪のヤジリン❄ No.441 解説
解説前の雑談
最近ニコリ様に投稿を考えています!こんばんは!
今回は21×21(=441マス)のハバネロヤジリンを解説していくのですが、正直大きすぎてグダグダになっている部分もありますがお許しください🙏
また、ハバネロの問題を解説していくのでたいへん~アゼン程度の問題は解ける人を対象としています
なるべく分かりやすく解説したいつもりですが、分からない部分があればTwitter(現X)のDMなどで気軽に聞いてください!
それでは、元気よく解説に移ります!
解説

先に解きたい方はこちら

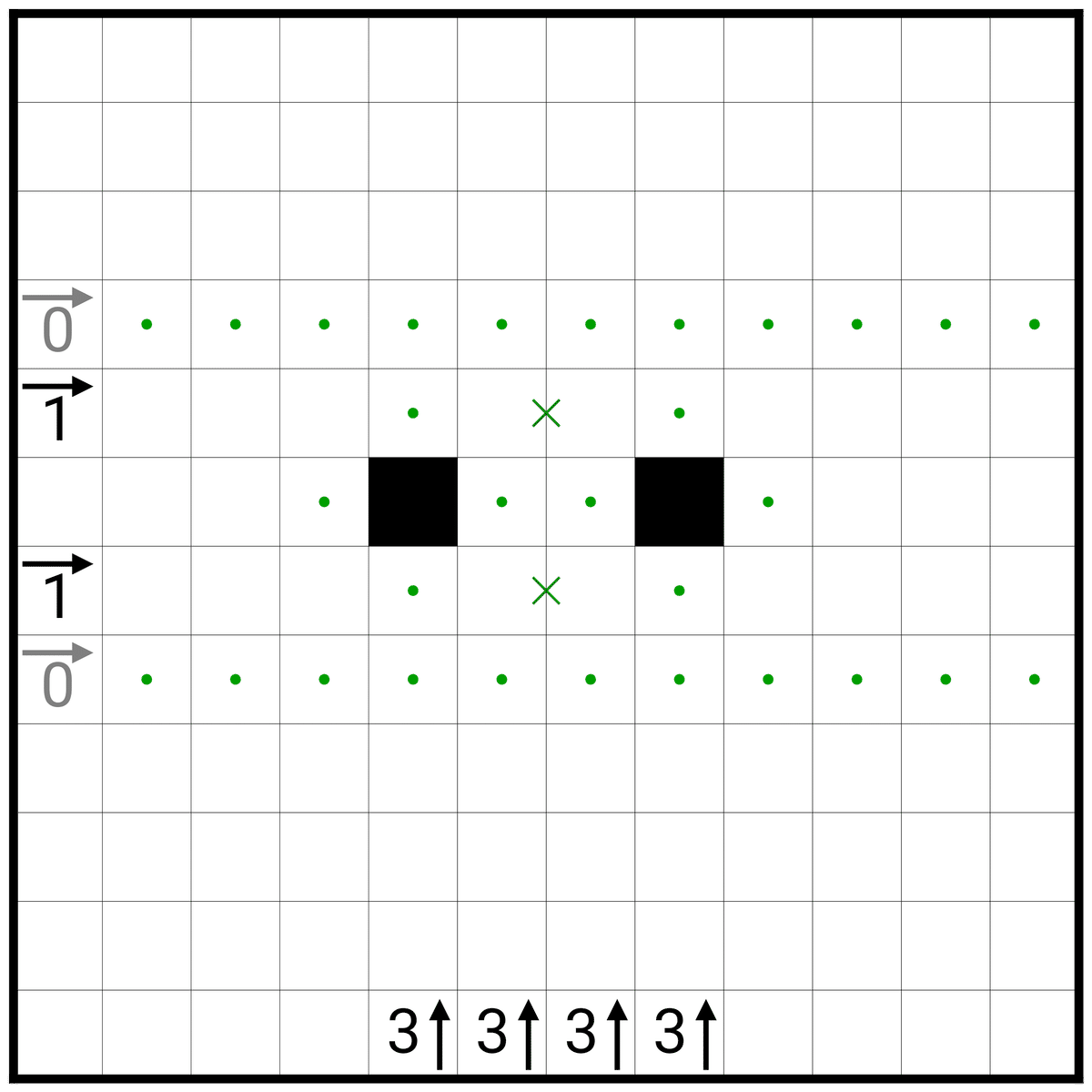
まずは初手で分かるところを埋めました!
この時点で分からないかも…と思った方はそっと閉じて1ヶ月後とかにまた見ましょう
黒マス1in1×2の部分には×の印をつけています
次に、この問題のメインである3↑四つの部分について考えます!

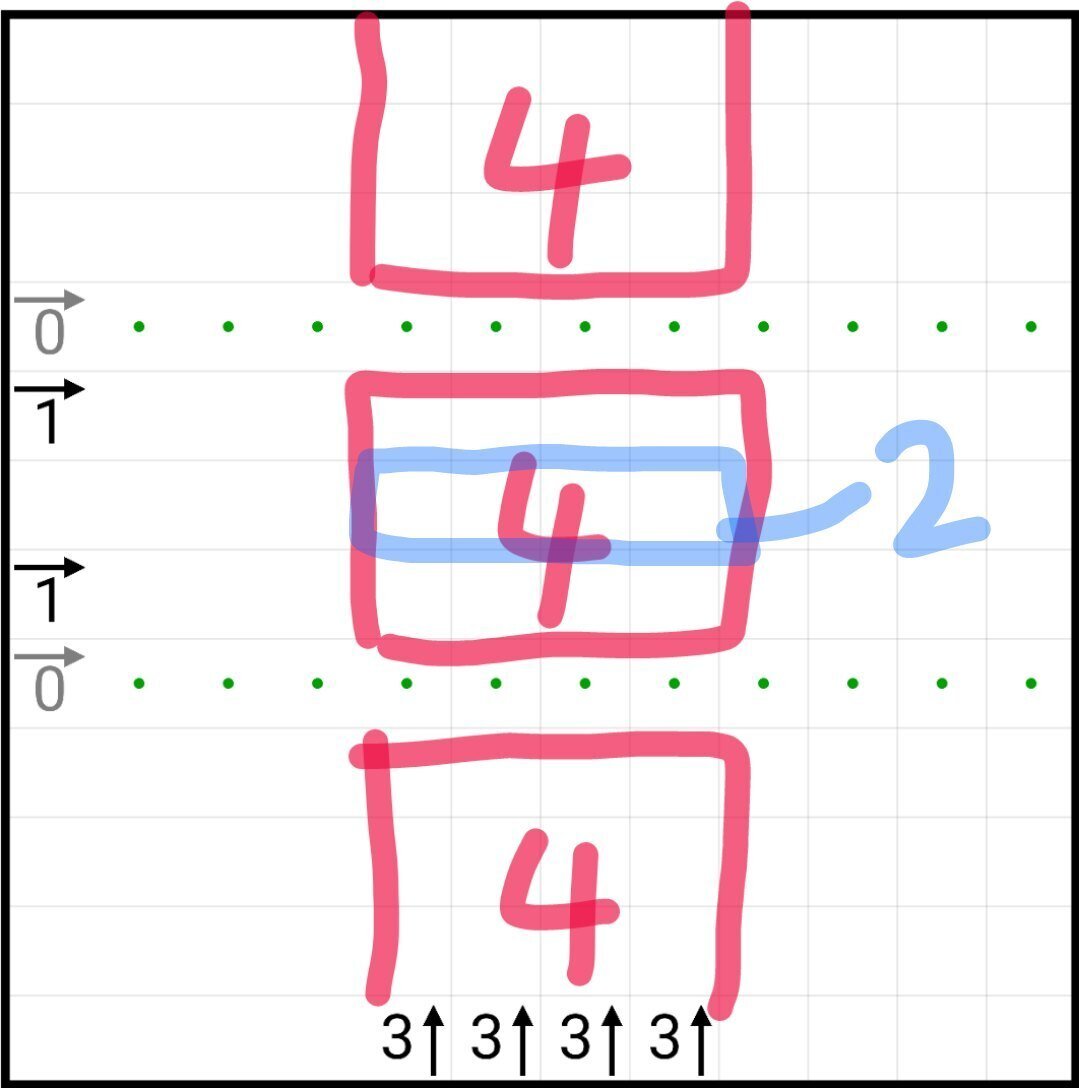

まず上、中央、下には黒マスはそれぞれ4つずつ入ります(5つ以上入れることはできません)
また、中央の1→二つのおかげで、青の部分には黒マスが2つ入ることが分かります!
青の部分に1つ飛ばしで黒マスを入れると行き止まりができて破綻してしまうので、最後の画像のように決まります!




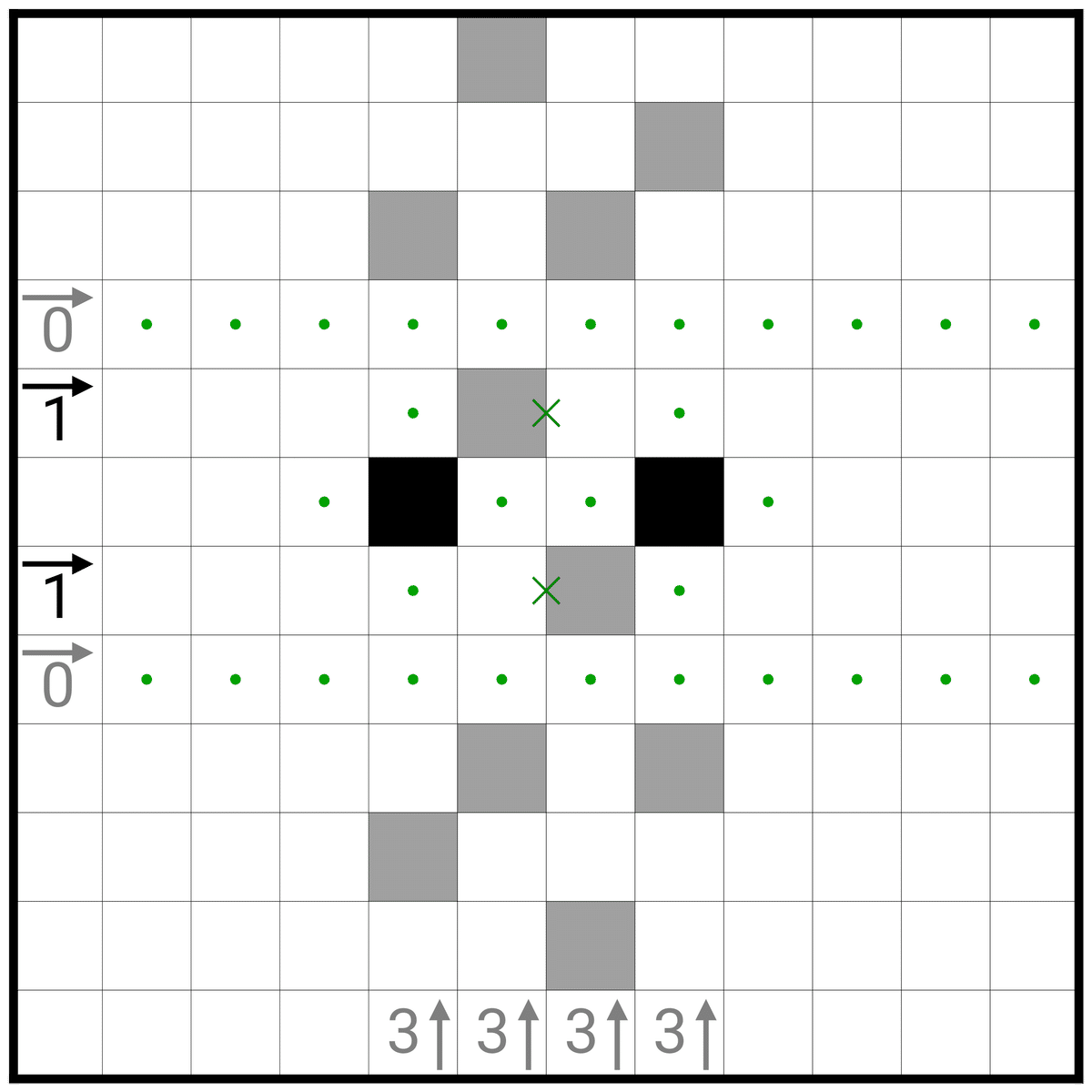
(1、2枚目)3↑の端に黒マスが1つ飛ばしで2つ入るとすると、反対側の領域(画像では上側)で黒マスが4マス入らないので破綻します!よって、2枚目のように黒マスが占めることがわかります!
(3、4枚目)充填で考えると3枚目のように黒マスが占めることが分かります!また、4枚目のように黒マスが2マス飛ばしで2つ入るとすると残り2つの黒マスを入れられないので、3枚目の青の領域では1つ飛ばしで黒マスが入ることが分かります!


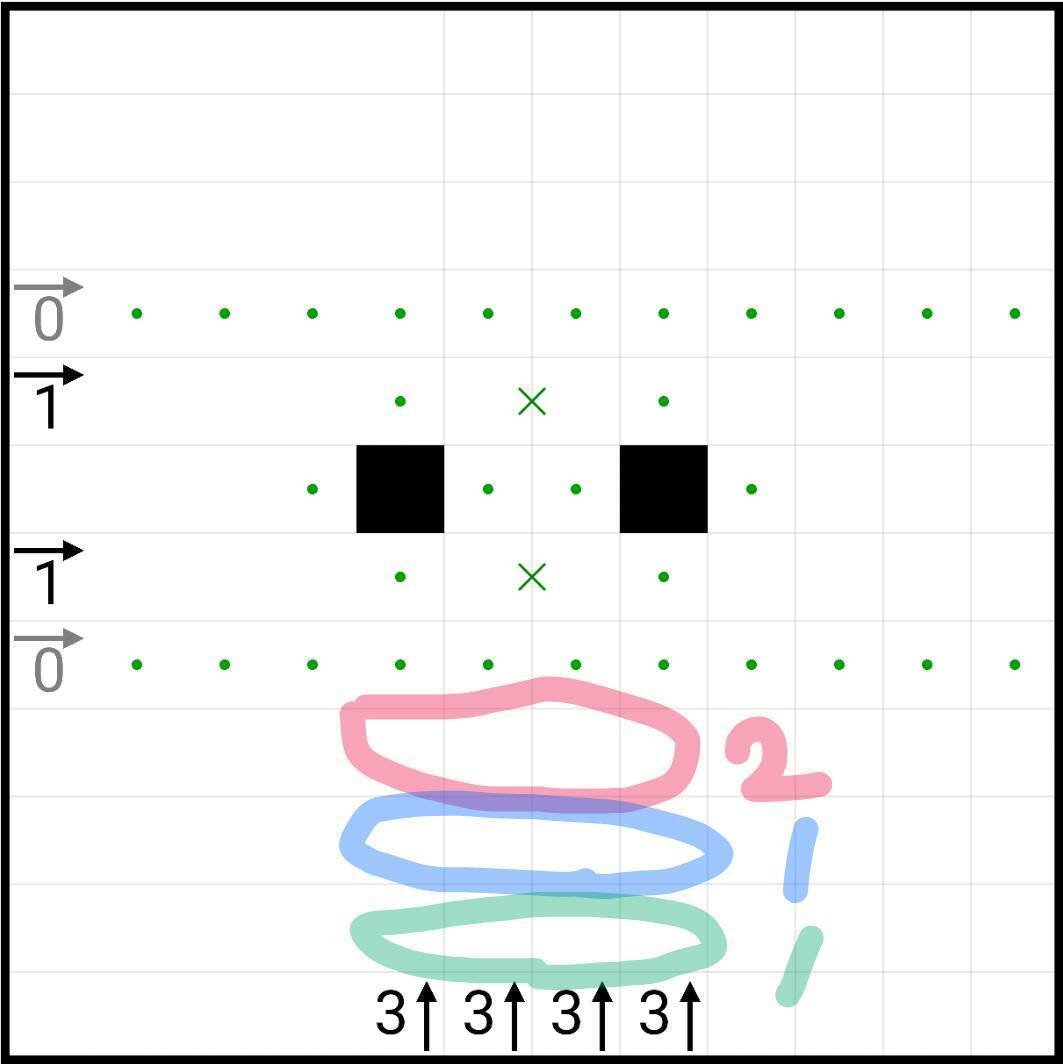
おわん型にならないように黒マスを入れていくと、2枚目か3枚目の2択になることが分かります!
また、4枚目のように黒マスが入ることがわかります!この予約を使って進んでいく形になります!
正確に把握できなくても、下側(もしくは上側)がこんな形で黒マスが入るんだな〜という事が分かっていれば大丈夫です!
(実はこの盤面だと破綻しています…この3↑地帯は風車を使って考えるといずれにせよ1本しか通ることができません!今回はその情報は必要ありません)
さて、問題の画像に戻りましょう



さっきどのように黒マスが入るかが分かったので、2パターンで共通する白マスと予約でわかる白マスから、2枚目、3枚目のように進んでいきます!


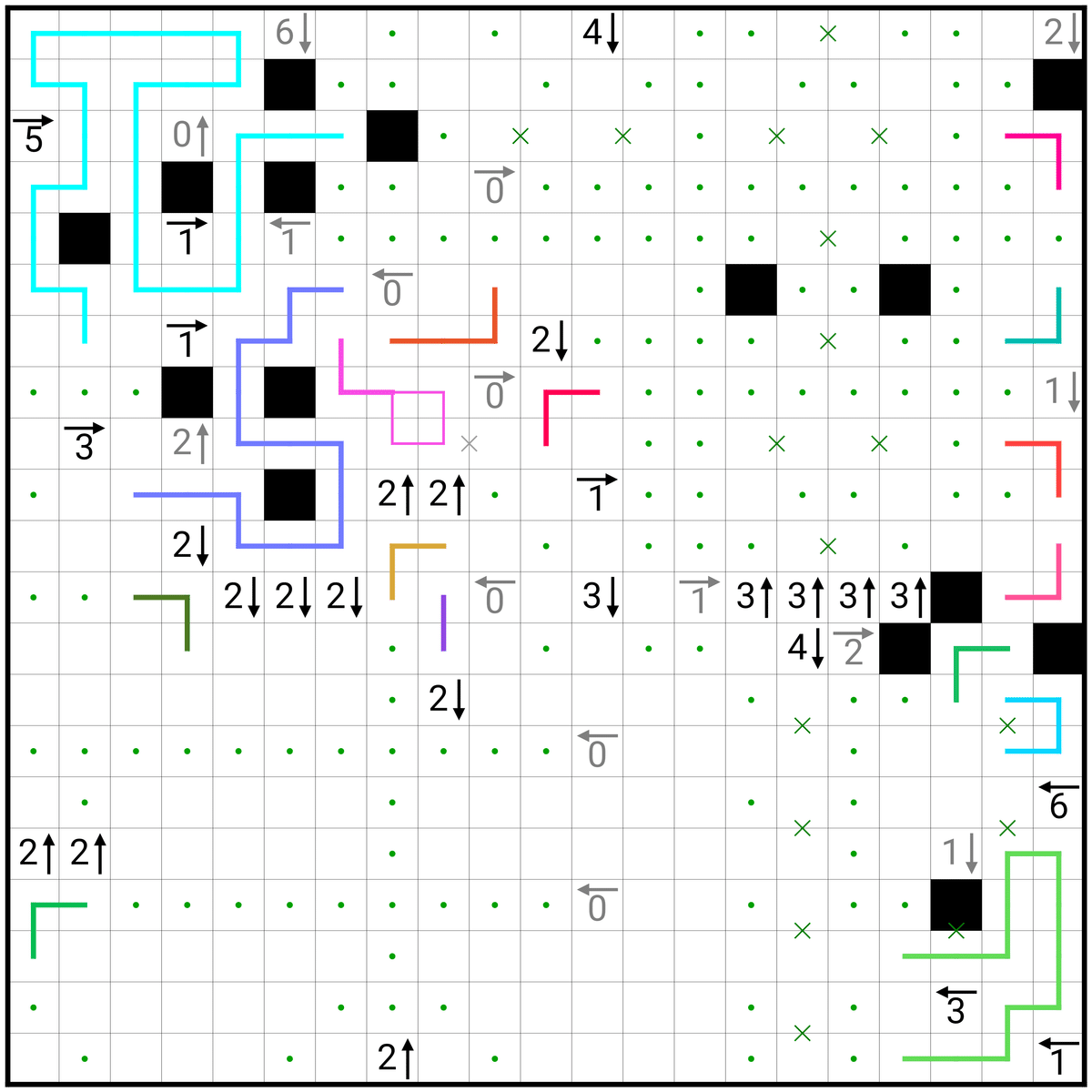

(ここの解説は軽くだけして進みます!ついてこれてなかったらごめんなさい アイス食べたい🍨)


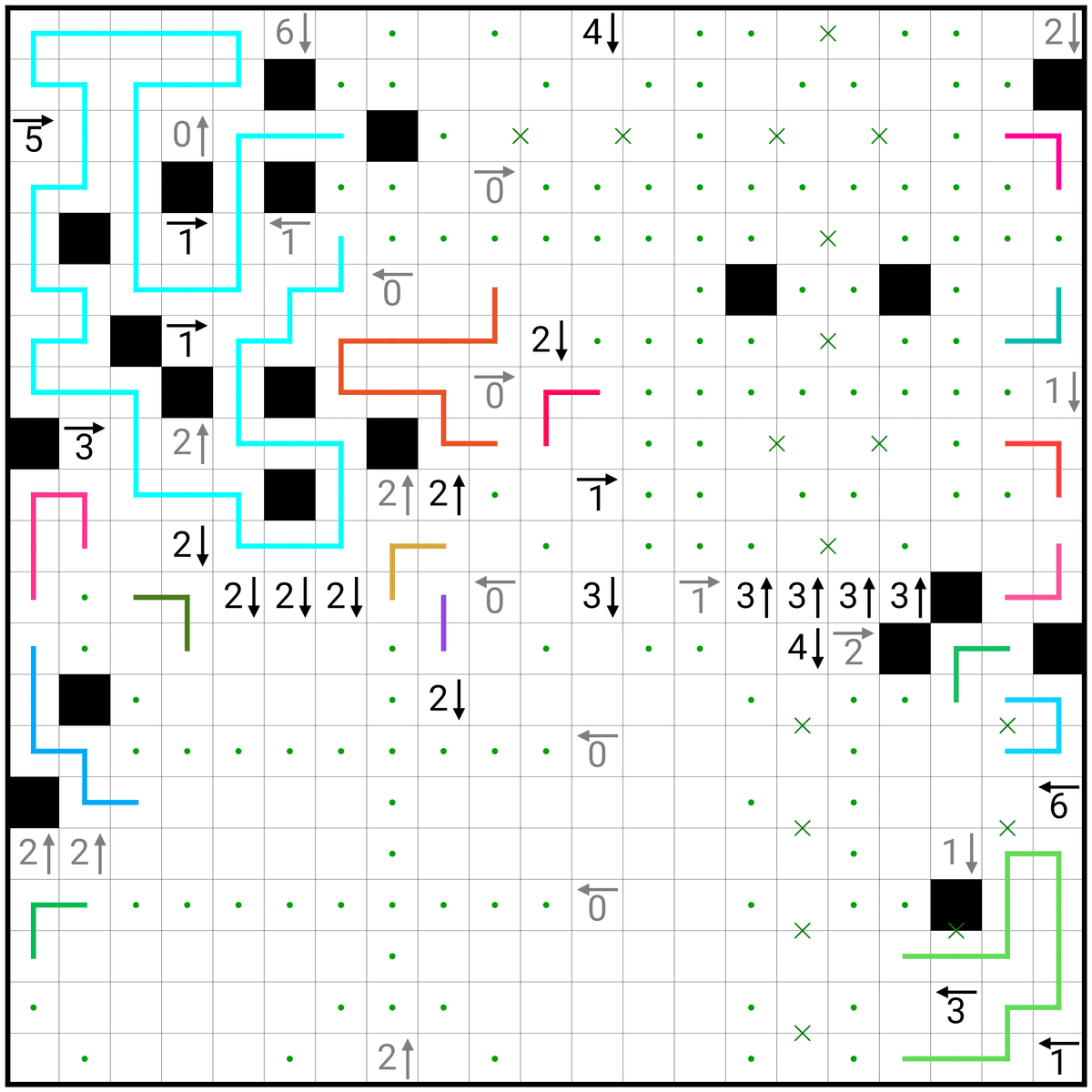
2↑が決まり、さらに3↑地帯で黒マスが2マス入ることがわかっているので、R9C3(上から9、左から3マス目)は白マスになることが分かります!そこからは偶奇で3→の左側に黒マスが入り、1枚目のように決まります!
さらに、辺に接する2×2には1マスまでしか入らないので、3枚目のように決まっていきます!





(1、2枚目の説明は割愛)
3枚目のようにR3C10に黒マスが入ると、その黒マスと4↓の間が隘路になって小ループができてしまいます!よって5→の黒マス3つを埋めることが出来ます!
また、4枚目のようにR5C9が白マスだとすると小ループが出来てしまうので、5枚目のように伸ばすことが分かります!

この形覚えていましたか?



3↑地帯の一方ではすぐに破綻することが分かるので、もう一方を埋めて黒マスが大量に決まります!4枚目までは簡単に進めることが出来ます!



1枚目の赤い四角の部分で風車の定理を使うと、2枚目のように伸びて3枚目まで進むことが出来ます!画像で説明してしまってあんまり言うことがなかった!!


1枚目はシンプルループの要領で伸ばすことができました!
R8C13に着目すると2方向が塞がっているのでそこを起点に2枚目まで伸ばすことが出来ます!



1枚目は偶奇から上と下の2マスを決めることが出来ます!(厚揚げスペシャル)
2枚目のようにR17C16が黒マスだとすると回収できない白マスができてしまい破綻!よって3枚目のように決まります!(地味に偶奇!!もしてます!)

2×3には2マスまでしか入らない&辺に接する2×2には1マスまでしか入らないのでこのように×印をつけています


(1枚目)3↓の×から中央上にある2↓の候補を絞り込むことが出来ます!ただし、一番下の×印で正しく白マスを置かないとミスしてしまうので注意!
2枚目のように上側2つのどちらにも黒マスをいれてしまうと行き止まりができて破綻してしまうので、R20C11に黒マスが入ります!



1枚目の赤い領域に黒マスがないとすると、左から6マス目の2↓が入らなくなってしまうので、赤い領域には1つ黒マスが入ります!
右下の3←はそこで予約されるので、他の部分は全て白マスとなり3枚目まで進めることが出来ます!


1枚目のように黒マスが置かれると仮定すると下の線が出れなくなり破綻するので、2枚目のように黒マスが入ることがわかります!




(1、2枚目)R16C5に黒マスが入るとすると、左から6マス目の2↓が破綻するので、R16C4に黒マスが入ります!
(3、4枚目)左から5マス目の2↓について考えるとR17C5かR19C5に黒マスが1つ入りますが、R17C5に黒マスが入ると左から6番目の2↓に黒マスを入れられないのでR19C5に黒マスが入ります!
もう終盤です!!あとは流れで決められるので、画像だけの解説になります
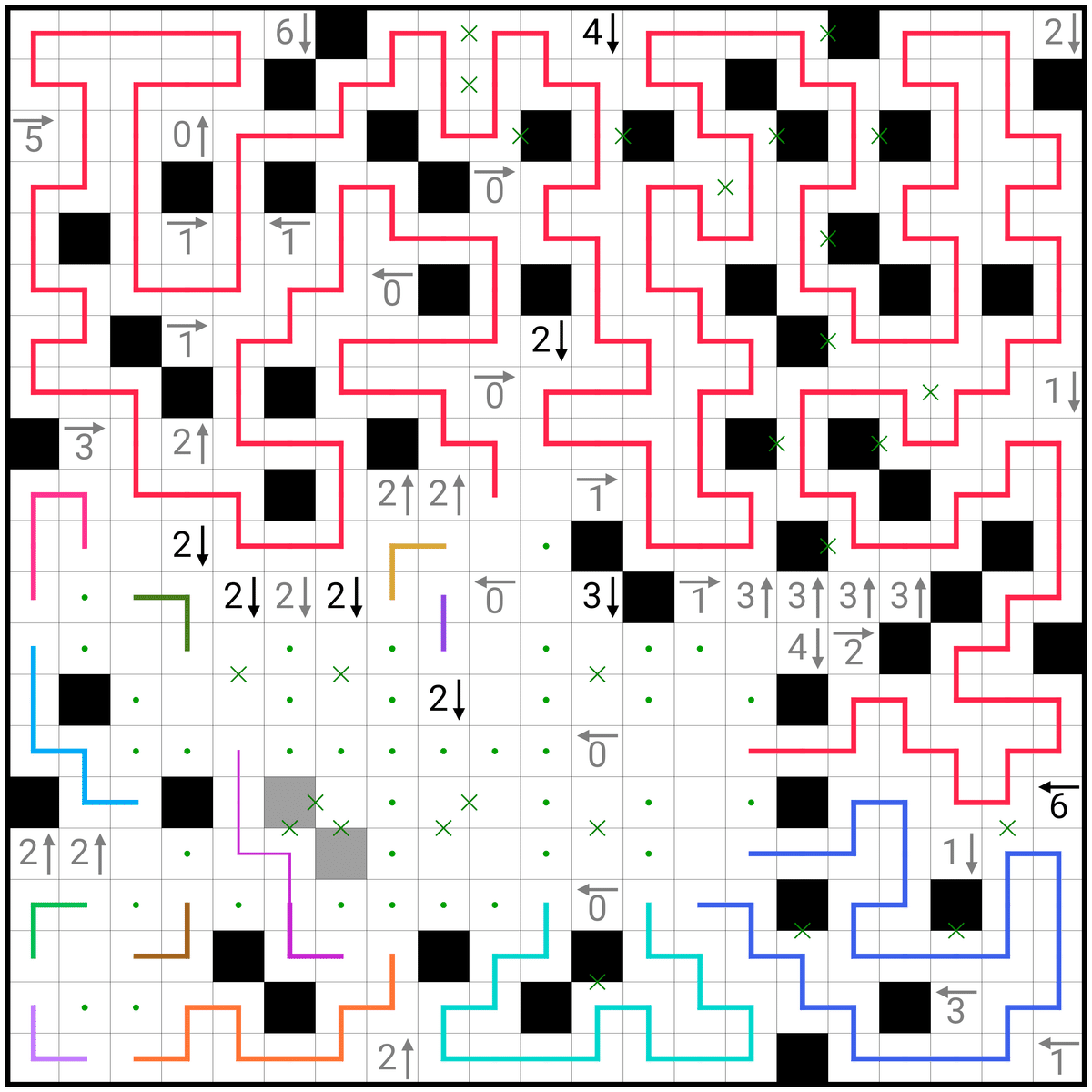




お疲れ様でした!!!!!
あとがき
かなり長くなりました!後半雑になったり勝手に付け足したりしてて申し訳ないです!!
3↑地帯の1本しか通らないということに気づいた嬉しさで作った問題で、実は4以上でも似たように作ると奇数本通るようになっています!知らないと難しい情報なので今回はそれを知らなくても解けるようにしました!
拙い説明でしたが少しでも伝わっていただけたら嬉しいです!
それではおつゆき〜❄
❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄
TwitterやPuzzle Squareにいろんなパズルを投稿しています!ぜひたくさん解いていってください!
また、不定期でヤジリンの大会を開いてたりするのでそちらもぜひ!
❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄
Twitter→@Yuyuki1112
https://twitter.com/Yuyuki1112?t=Is7E5nMpYSUpxl-m5qxm8A&s=09
Puzsq→Yu-ri
