複雑な式2 内積
今回は複雑な式を内積で捉えていこうという内容です.
そのためには,まず内積をきちんと理解しましょう.




応用するためのポイントとしては,同じ内積に対して,2つの座標軸でみてやるということです.OAの座標軸で見た場合と,OBで見た場合の両方を考えていくと良いです




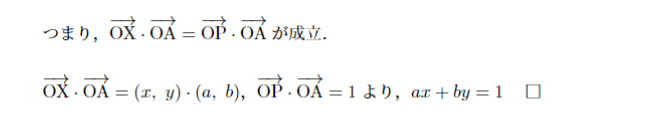



ここまでが,内積のウォーミングアップです.では,複雑な式をどうやって内積の問題に落とし込むか見ていきましょう.





ax+by=1というのを内積で表現すると,次の図が直感的に分かるようになると良いですね

今回は複雑な式を内積で捉えていこうという内容です.
そのためには,まず内積をきちんと理解しましょう.




応用するためのポイントとしては,同じ内積に対して,2つの座標軸でみてやるということです.OAの座標軸で見た場合と,OBで見た場合の両方を考えていくと良いです




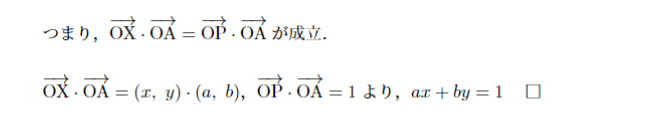



ここまでが,内積のウォーミングアップです.では,複雑な式をどうやって内積の問題に落とし込むか見ていきましょう.





ax+by=1というのを内積で表現すると,次の図が直感的に分かるようになると良いですね
