
【機械学習】「Pythonではじめる機械学習」
「Pythonではじめる機械学習」
Andreas C. Muller、Sarah Guido著
基本的には、本書から勉強したことを自身の経験に基づいて記載するようにします。そのため、本書に記載されているデータの確認ステップやプログラムが内容と異なることが多々あるのでご留意ください。
【注】
※下記のGitHubを参考にします。
(コピペで自身のPythonに張り付ける形で問題ないと思います!正直、下記のGitHubは大変わかりやすく、そちらをみながら勉強するのがいいと思うので、私の分はあくまでも参考程度に。。。)
※使い慣れていることもあり、エディタはSpyderを使用します。
【目次】
第1章 はじめに
1.1 機械学習で解決可能な問題
機械学習における分野では、主に2種類、得意とする分野がある。
〇教師あり学習
望ましい出力の結果が分かっている場合の学習方法。
(例)
・手書きの数字から郵便番号を読み取り
・医療画像からの腫瘍の良性・悪性の診断
・顧客の口座の取引データから不正利用されている口座の検出
〇教師なし学習
望ましい出力の結果が分からない場合の学習方法。
(例)
・多数のブログへのログイン履歴からのトピックの特定
・顧客の嗜好のグルーピング
1.2 タスク、データを知る
上記の問題を解決するために、機械学習モデルを構築するわけだが、まずは
「モデルを構築するうえで必要なデータセットはそろっているのか」
「不要なデータセットは何か」
「どのアルゴリズムを使用するのが最適か」
を判断するために(そもそも機械学習を使用せずとも、簡単な統計量の算出だけで解決する問題も少なくない)データセットをしっかり確認する必要がある。
1.3 なぜPythonなのか?
機械学習を行う上で、RやC言語ではなく、Pythonを使うメリット何なのか。
①豊富なパッケージが日々開発されており、最新のアルゴリズムを使用することができる
②オブジェクト指向型言語であるため、初心者でも扱いやすい言語である
③大手企業(GoogleやMicrosoft)ではPythonが主流であるため、多言語に比べ開発や技術の更新が活発である
特に③について、最近ではRでも機械学習に関するパッケージが複数開発されており、比較的最新のアルゴリズムを使用することは可能であるようなのだが、社会のトレンドを見る限り、機械学習を行っている多くの企業がPythonを使用しているため、互換性の観点からも、私はPythonを推奨したい。
1.4 scikit-learn
それでは、早速Pythonを使用する準備を始めていこう!
パッケージやモジュールについての詳しい話は、別の記事でまとめようと思います。(【機械学習】機械学習やPythonの用語集、暗黙の了解集 をご参照)
本書において、scikit-learn(サイキットラーン)を使用しているので、まずはscikit-learnのインポートから行う。
In:
import sklearn
print(sklearn.__version__)Out:
1.4.2・import sklearnでsicit-learnをインポート
・print()で()のなかを表示する。パッケージ名.__version__ でパッケージのバージョンを確認。
【tips】もし上記でインポートができない場合は、コマンドプロンプトで確認。
conda prompt(コマンドプロンプト)を開き、conda list(pip list)でsklearnが表示されているか確認。
もしない場合→conda install sklearn (コマンドプロンプトの場合は、pip install sklearn)
もしある場合→Pythonのインタープリターが自身が使用している(と思い込んでいる)Anacondaが保存されているファイルと同一か確かめてみよう。
Spyder→設定→Pythonインタープリター→Spyderコンソールで使用するPythonインタープリターの選択 「〇デフォルトと同じ」or「〇以下のPythonインタープリターを使う」
デフォルトと同じでは、Spyderがインストールされている場所に存在するインタープリターが選択される。「〇以下のPythonインタープリターを使う」を選択しAnacondaを保存しているファイルパスを選択してみよう(私は「ある場合」で解決した))
1.5 アイリスのクラス分類
本書では、機械学習や統計学で古くから利用されているアイリスのデータセットを用いる。アイリスとはフランスの国花で、下記のような花である。
目標は「新しく見つけたアイリスの種類を予測するために、種類が分かっているアイリスの測定値を用いて機械学習モデルを構築する」こととする。
(このようなモデルを一般的に「クラス分類モデル」と呼ぶ。)
1.5.1 データを読む
まずはデータをPythonに読み込む。
sklearnに既存であるらしい(この本を読むまで知らなかった)ので、下記コードで読み込んでみよう。
In:
from sklearn.datasets import load_iris
#データを読み込む
iris_dataset = load_iris()
#データセットのキー(データセットの簡単な説明)を表示
print("Key on iris_dataset:\n{}".format(iris_dataset.keys()))Out:
Key on iris_dataset:dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module'])・sklearnのload_iris()関数で読み込み
・\nで改行。{}の中にformat()のカッコ内の結果を表示。keys()関数でデータセットのキーを返す。
本書では複数関数でデータセットの基本的な概要を確認している。本書では割愛するが、下記については確認してみてもと思う。
・type()関数:データセットの型を確認。
・shape関数:行列数を返す。
1.5.2 訓練データとテストデータに分割
機械学習モデルを構築するにあたり、実際にモデルの精度を確かめるためにテスト(検証)を行う必要がある。
モデルを構築する際、モデルを構築するために使用するデータと精度を検証するために使用するデータにあらかじめ分けることが多い。
モデル構築用データを訓練データ、検証用データをテストデータと呼ぶ。
scikit-learnには、訓練データとテストデータを分けるためのtrain_test_split関数があるので、今回はそれを使用して両データに分けてみよう。
In:
from sklearn.model_selection
import train_test_split
X_train, X_test, y_train, y_test
= train_test_split(iris_dataset['data'], iris_dataset['target'], random_state=0)・X_train, X_test, y_train, y_test...train_test_split関数では、
X_train(特徴量の訓練データ)
X_test(特徴量のテストデータ)
y_train(目的変数の訓練データ)
y_test(目的変数のテストデータ)
の四種類が作成されるので、左辺に4つのデータセットのボックスを作成するイメージ
(iris_datasetでは、['data']に特徴量が、['target']に目的変数が格納されているみたいですね。)
・train_test_split(データセット(特徴量),データセット(目的変数))
デフォルトでは75%:25%に分けられる
・random_stateは繰り返し分割する際、分割後の数にSeedを与える。=0でも1でも、いい。(その数のseedが与えられる。)逆に言うと、=の数を変えると、分けられ方が変わる。
上記のプログラムを実行した結果、下記のように75%:25%でデータが分かれていることが分かる。

また、4つの特徴量の名前を確認してみると、
In:
print(iris_dataset.feature_names)Out:
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']と確認できる。
sepal…ガク
petal…花弁
それでは、データを観察してみよう。
データを観察するとき、何を観察すればいいだろう?(平均や分散?散布図?ヒストグラム…??)
これも実際は、観察するデータによって定量的に判断すべきだが、私は図示するとわかりやすいなとよく思う。
今回、本書では、各特徴量同士の散布図を確認している。
(すべての特徴量の相関を同時に確認する方法をペアプロットと呼ぶ。)
In:
iris_dataframe = pd.DataFrame(X_train, columns=iris_dataset.feature_names)
iris_dataframe['target'] = pd.DataFrame(y_train)
sns.pairplot(data = iris_dataframe, hue="target", vars=iris_dataset.feature_names)
plt.show()Out:

・pd.DataFrame()でX_trainの型をデータフレーム型に指定し、columns=でコラム名を設定(snsはndarray型は読み込めないため)
・sns.pairplot(data = データフレーム, hue=色彩(一般に目的変数を与えることで目的変数に沿った色彩になる??), vars=プロットする数値データ名。指定しなければ全数値データをプロット)でペアプロットの作成
この結果から、花弁の長さと幅とガクでよく分離していることが分かる。
⇒うまく分離している特徴量があるため、機械学習モデルの分類モデルに当てはまりやすいことが推測できる。
1.5.3 k-最近傍法(さいきんぼうほう)
ここでは、k-最近傍法を使用して分類を行う。
k-最近傍法とは、ある点から近いデータに対してフラグを観測することで、ある点に関する類推をするモデル。詳細については下記を見てみよう(他力本願)。

In:
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train, y_train)・knnにKNeighborsClassifier()を代入
・n_neighborsの場合は一番近いデータのみ同じクラスとする。最近傍法。
・knn.fit(X_train, y_train)
さて、このモデルを使って、ラベルが分かっていないデータに対して予測を行ってみよう。
In:
y_pred = knn.predict(X_test)
print("Test set predictions:\n{}".format(y_pred))Out:
Test set predictions:[2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0 2 1 0 2 2 1 0 2]上記で作成したモデルの評価を行う。
In:
print("Test set score: {:.2f}".format(knn.score(X_test, y_test)))Out:
Test set score: 0.97正解率が97%とでた。目的変数の内容にもよるが、一般的には0.8以上であれば高いと考えることが多い気がするので、今回では非常に高い予測精度が算出されている。
第2章 教師あり学習
教師あり機械学習は目的変数によって大きく2つにわけることができる。
離散型データが目的変数の場合は「クラス分類(classification)」を活用し、連続データが目的変数の場合は「回帰(regression)」を活用する。
データの種類によっては、たとえ目的変数が連続データでもクラス分類(or 回帰)のほうが都合がよい時もあるので、最終的なモデルの判断は上記に記述した通りデータをよく確認する。
しかし、教師あり学習に共通して言えるのは、実務におけるモデルの精度の高さを最も重視しないといけないことである。これをどんなデータにも当てはめることができるという意味で汎化(はんか)できているモデルと呼ぶ。
訓練データから十分な学習ができていなかったり(適合不足)、訓練データに対して当てはまりがよすぎたりすると(過学習)、テストデータ(実務で使うデータ)に対して汎化できていないことになる。
教師あり学習の大きな流れは下記の通り。
データをモデルが学習するためのデータ(訓練データ)とモデルの精度を評価するためのデータ(テストデータ)に分ける。
訓練データを使ってモデルを作成
作成したモデルの精度をテストデータで確認
説明変数の選択、特徴量をモデルに合った形に変形する(特徴量エンジニアリング(4章で説明する))などしモデルをチューニング
2に戻る
上記を繰り返し精度の高いモデルを作成する。
2.1 連続データを予測するモデル
まずは連続データを予測するモデルを見てみよう。
2.1.1 線形回帰
代表的なモデルに線形回帰モデルがある。線形回帰モデルとは目的変数(予測したい値)と1つ以上の特徴量(入力データ)との間に、線形の関係があると仮定してデータを予測するための統計的手法である。特徴量が一つなら単回帰モデル、複数なら重回帰モデルという。基本的には重回帰モデルを扱う。
連続データを予測するモデルの例を見てみよう。データは下記にあったハンガリーの2006~2016年までの天候データを使用する。(このnoteではあくまでも回帰分析の方法に着目したいので、データのダウンロードは特にしないで大丈夫です。)
上記のデータを使って気温や降雨量などの特徴量から風のスピードを予測するモデルを作成してみよう。
目的変数↓
Wind Speed (km/h): 風速
特徴量↓
Temperature (C): 気温(摂氏)
Apparent Temperature (C): 体感温度(摂氏)
Humidity: 湿度
Wind Bearing (degrees): 風向(度)
Visibility (km): 視程(キロメートル)
Pressure (millibars): 気圧(ミリバール)
(本当はデータの特徴をヒストグラムで確認したり、単回帰して特徴量と目的変数の関係の確認などを確認 などの前処理を経て重回帰分析を行うのだが、一旦ここでは細かいところはおいておく)
データの中身は以下の通りである。

まずは、上記のデータを訓練データとテストデータに分ける。
from sklearn.model_selection import train_test_split
X = df[['Temperature (C)', 'Apparent Temperature (C)', 'Humidity',
'Wind Bearing (degrees)', 'Visibility (km)',
'Pressure (millibars)']]
y = df['Wind Speed (km/h)']
# 訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
Xに特徴量を、yに目的変数をいれてそれぞれ訓練データ:テストデータ=8:2になるように分割した。
sikit-learnにはtrain_test_split関数という訓練データとテストデータに分けてくれる使い勝手の良い関数がある。
次に、すべての説明変数を使って回帰モデルを訓練する。その後、テストデータで目的変数(風速)を予測しモデルのパフォーマンスを確認してみよう。
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
# 線形回帰モデルの作成
model = LinearRegression()
# モデルの訓練
model.fit(X_train, y_train)
# テストデータで予測
y_pred = model.predict(X_test)
# モデルのパフォーマンスを評価
mse = mean_squared_error(y_test, y_pred)
print(f"Mean Squared Error (before feature selection): {mse:.3}")
# 訓練セットとテストセットのR²スコア
r2_train = model.score(X_train, y_train)
r2_test = model.score(X_test, y_test)
print(f"R² Score (train set): {r2_train:.3}")
print(f"R² Score (test set): {r2_test:.3}")
Out:
Mean Squared Error (before feature selection): 24.3
R² Score (train set): 0.468
R² Score (test set): 0.417これは、説明変数をすべて入れたときのテストセット(モデルの性能を評価するために使用されるデータセット)のMSE(平均二乗誤差)が24.3だったことを示している。MSEの値を評価する際には、データのスケール や モデルの目的 を考慮し、他のモデルや指標と比較する際に使用する。(MSEの詳細は下記ご参照)
また、R^2(決定係数)が訓練セットで0.468、テストセットで0.417であった。R^2はモデルのデータへの当てはまりの良さを表す指標であり、0~1の値を取る。1に近いほど当てはまりがよいとされるが、MSEと同じで、それ単体での使用というよりは、複数個のモデルの比較時に使用されることが多い。(R^2の詳細は下記ご参照)
実務においては、上記の方法によるモデルの作成に加えて、5.1で詳しく説明する「交差検証」を行うなどして頑健性を確保したモデルを作成する。
y_pred(予測結果)とy_test(テストデータの目的変数)を比較したところ、あまり精度の高いモデルとは言えないのが現状である。

全然予測できてない
2.1.2 ラッソ回帰(L1正則化)・リッジ回帰(L2正則化)
上の例では、6つの特徴量をすべてを使用してモデルを作成した。しかし、例えば特徴量の候補が100個あったらどうしよう。基本的にはモデルの説明性を考えると、本当に大切な特徴量に絞り込むのが妥当である。また、多重共線性という、説明変数間で相関が高いもの同士がモデルに入っていた場合、計算時にエラーが起こる問題も発生してしまう。
一体どのように説明変数を絞り込めばよいのか。
一つの例として4.2.4で詳しく説明する「L1正則化」や「L2正則化」項で特徴量を削減する方法がある。(Logistic RegressionではデフォルトでL2正則化が行われることに留意。)
そのほかには、説明変数をすべて入れたあと、R^2スコアなどのモデルの精度確認指標と各説明変数間の相関係数を確認しながら、一つずつ手作業で落としていく方法もある。(より高い精度が求められる時などは、一つずつ手作業で落とす作業と正則化項の使用の併用で説明変数を絞り込むことが多いと思う。)
2.2 2値分類を予測するモデル
次に離散型データを目的変数とした場合の予測モデルを見てみよう。
実務上では「商品の『不良品』と『製品』を区別するモデル」や「顧客取引の異常性を検知するモデル」などの「あたり(黒、不良品、1などなど様々な言い方がある)」か「はずれ(白、良品、0)」かの2値を予測するモデルがある。
ここではsikit-learnライブラリにある有名な「乳がんデータセット(Breast Cancer Dataset)」を使用する。これは、乳がんの腫瘍を計測し、それぞれに害のない腫瘍を意味する「良性(benign)」と癌性の腫瘍を意味する「悪性(malignant)」のラベルがついている。ここでのタスクは測定結果から腫瘍が良性か悪性か予測するモデルを作成することである。
from sklearn.datasets import load_breast_cancer2.2.1 ロジスティック回帰
まず、2値分類モデルの中でもっとも有名なものの中にロジスティック回帰モデルがある。ロジスティック回帰モデルは名前に反して回帰アルゴリズムではなくクラス分類アルゴリズムであることに留意しよう。
ロジスティック回帰は、以下の式で表されるシグモイド関数(ロジスティック関数)を使用して、予測値を0から1の範囲(確率)に変換する。

P(y=1):与えられた特徴量 に対して、クラス1(たとえば「はい」や「成功」)である確率
w⋅x:線形結合(重み w と特徴量 x の内積)
b:バイアス(切片)
e:自然対数の底
予測値はあたり確率で算出される。この確率に対して閾値を決め、その閾値以上なら「あたり」閾値以下なら「はずれ」と予測する。
cancer dataでロジスティック回帰モデルを作成してみよう。
In:
# 必要なライブラリをインポート
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib.pyplot as plt
# 1. データの読み込み
data = load_breast_cancer()
X = data.data # 特徴量
y = data.target # ターゲットラベル
# 2. データの分割 (訓練用とテスト用)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 3. ロジスティック回帰モデルの作成
model = LogisticRegression(max_iter=10000)
"""
max_iterは、モデルが収束しない場合に備えて、最大で何回の反復を行うかを決めるパラメータです。
収束する前にmax_iterに達すると、モデルはその時点で終了します。
"""
# 4. モデルの訓練
model.fit(X_train, y_train)
# 5. モデルの評価
y_pred = model.predict(X_test)
#accuracy = accuracy_score(y_test, y_pred)
# 6. 予測確率の計算 (クラス1の確率)
y_pred_prob = model.predict_proba(X_test)[:, 1]
# 7. ROCカーブの計算
fpr, tpr, thresholds = roc_curve(y_test, y_pred_prob)
# 8. AUCの算出
auc = roc_auc_score(y_test, y_pred_prob)
# 9. ROCカーブのプロット
plt.figure()
plt.plot(fpr, tpr, label=f'ROC curve (AUC = {auc:.4f})') #AUCを図中に記述
plt.plot([0, 1], [0, 1], 'k--') # ダイアゴナルライン
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend(loc="lower right")
plt.show()Out:

上記のStep1~5を踏めば、誰でもロジスティック回帰モデルを作成できてしまう。
精度指標については「ROCカーブ」と「AUC」を用いた。
詳細は第4章で説明するのだが、ROCカーブは本当に陽性(TRUE POSITIVE(TP)/POSITIVEと予想された数)だった割合と偽陽性(FALSE POSITIVE/POSITIVEと予想された数)だった割合について、閾値を変化させていったときの両者の点をつなげて線にした図である。
AUCはROCカーブの下と45度線(まったく区別できなかった時の線)の面積を示す。1なら(閾値に関係なく)完全に分類できているモデルを示すこととなる。
この本では精度指標にaccuracy(正解率TPとTN(TRUE NEGATIVE)が全体に対してどれだけあったかの割合を示す)が使われていることが多いが、実務においては(1)扱うデータが不均衡データが多いこと(陰性の割合が陽性の割合に対して異常に多い)や(2)陽性の正解率を特に重視することが多いこと、(3)閾値に依存しないこと などからAUCを使うことが多い。
今回のモデルではAUC=0.99と非常に高い精度のモデルが算出できた。
【メモ】教師あり学習で特に注意すべきこと
ここで、教師あり学習において一つ特に注意すべきことを上げよう。上記のようにモデルを訓練したり、その予測をしたりする際、すでに定義されている関数を使って簡単に計算できてしまう。
注意すべきなのは、y_test、y_pred(モデルが予測したクラスラベル)、y_pred_prob(ポジティブクラスに属する確率)を、しっかり関数に当てはめることである。
例えば、# 8. AUCの算出 では auc = roc_auc_score(y_test, y_pred_prob)
とした。しかし、roc_auc_score(y_pred_prob, y_test)でもroc_auc_score(y_test, y_pred)でも計算はできてしまう。しかも、この点は意外とだれも気付かない。
roc_auc_scoreはy_testに対して、y_pred_prob(確率)を当てはめることで、閾値に関係ない(様々な閾値の)ROCカーブに基づいたAUCを計算してくれる関数である。y_pred_probのところを間違えてy_predとした場合、y_predは閾値によってラベル付けされた値なので、閾値に依存した正しくないROCカーブが作成されてしまう。
上記の例で、y_pred_probの箇所をy_predにしてみると
In:
# AUCの算出
auc = roc_auc_score(y_test, y_pred_prob)
print(f'AUC: {auc:.4f}')
auc_fault = roc_auc_score(y_test, y_pred)
print(f'AUC_fault: {auc_fault:.4f}')
Out:
AUC: 0.9977
AUC_fault: 0.9464AUCの値が変化してしまう。(間違った計算結果を示すこととなる。)
ROCカーブも、閾値に依存した形になってしまう。(ある閾値以上でがくっとTPとなる)

上記のようななめらかでないROCカーブが描写された際は、今一度自身の計算方法が正しいか確認しよう。
2.2.2 サポートベクトルマシン(SVM)
データポイントを2つのクラスに分類する最適な分離超平面(hyperplane)を、2つのクラスの間にある「マージン(余白)」を最大化するように見つけ分類するモデル。
カーネルトリックを使って、データを高次元空間にマッピングし、非線形分離が可能な点でロジスティック回帰モデルよりも使い勝手が良いことがある。線形分離できないデータに対しても高いパフォーマンスを発揮する。
カーネルトリック(線形分離できないデータを高次元空間にマッピングすることで線形分離可能にする方法)には様々な種類があるが、データに非線形なパターンが存在する場合、まずはRBFカーネルを試すのが一般的。データを無限次元にマッピングする効果がある。


cancer dataでSVMを作成してみよう。
In:
#train_test_splitまではロジスティック回帰モデルと同じ
from sklearn.svm import SVC
# 3. SVMモデルの作成 (確率予測を有効にする) マージンを最大化する境界線を引くことで分類するモデルだが、オプションでデータポイントがその分類に分類される確率が算出できる
model = SVC(probability=True)
# 4. モデルの訓練
model.fit(X_train, y_train)
# 5. 予測確率の計算 (クラス1の確率)
y_prob = model.predict_proba(X_test)[:, 1]
# 6. ROCカーブの計算
fpr, tpr, thresholds = roc_curve(y_test, y_prob)
# 7. AUCの算出
auc = roc_auc_score(y_test, y_prob)
# 8. ROCカーブのプロット
plt.figure()
plt.plot(fpr, tpr, label=f'ROC curve (AUC = {auc:.4f})')
plt.plot([0, 1], [0, 1], 'k--') # ダイアゴナルライン
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend(loc="lower right")
plt.show()Out:
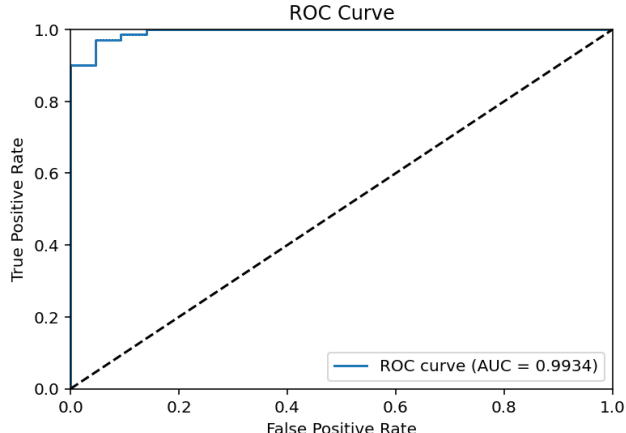
ロジスティック回帰モデルよりも少し精度が低くなった。これは、cancer dataは線形分離しやすいデータセットであることが伺える。
2.2.3 決定木
決定木モデルは、読んで字のごとく、特徴量に対してYes、Noでデータを分割し、樹上図を作成して目的変数を分類するモデルである。

各ノードの名称はよく出てくるので覚えよう。

Root Node(ルートノード): 決定木の一番上に位置し、データの分割が最初に行われる場所です。
Internal Nodes(内部ノード): ルートノードから分岐した各ノードで、特徴に基づいてデータが分割されていく中間のノードです。
Branches(枝): ノード間をつなぐ線で、決定木の分岐を示します。
Leaf Nodes(リーフノード): 決定木の一番下の層に位置し、最終的な予測結果やクラスラベルが割り当てられるノードです。
cancer dataで決定木を作成してみよう。
In:
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.metrics import accuracy_score, classification_report
# 3. 決定木モデルの作成
model = DecisionTreeClassifier(max_depth=5, min_samples_split=10, random_state=42)
# 4. モデルの訓練
model.fit(X_train, y_train)
# 5. テストデータに対する予測
y_pred = model.predict(X_test)
# 6. モデルの評価
accuracy = accuracy_score(y_test, y_pred)
report = classification_report(y_test, y_pred)
# 結果の出力
print('Classification Report:')
print(report)
# 5. 決定木の可視化
plt.figure(figsize=(25, 15)) # 図のサイズを設定
plot_tree(model, feature_names=data.feature_names, class_names=data.target_names, filled=True, rounded=True, fontsize=12)
plt.show()Out:
Classification Report:
precision recall f1-score support
0 0.93 0.93 0.93 43
1 0.96 0.96 0.96 71
accuracy 0.95 114
macro avg 0.94 0.94 0.94 114
weighted avg 0.95 0.95 0.95 114
今回の精度検証はあえてClassification Reportを使った。Classification ReportはクラスごとのPrecision(適合率)、Recall(再現率)、F1スコアを表示する。
決定木モデルには多くのハイパーパラメータがあり、これを調整することでモデルのパフォーマンスを向上させる。
max_depth(木の深さの制限)
min_samples_split(ノードを分割するための最小サンプル数) など
図についての説明
feature_names …データセットの各特徴量の名前を表示。
class_names …ターゲットクラスの名前(この場合は "malignant"(悪性) と "benign"(良性))
filled=True …ノードをクラスに応じて色付け。
rounded=True …ノードの角を丸くして見やすくする。
2.2.4 ランダムフォレスト
決定木モデルはどうしても訓練データを過学習してしまうため、陳腐化が早いという欠点がある。
ランダムフォレストは過学習を抑制するために、少しずつ異なる複数の決定木をたくさん集めて作成するモデルのことである。(ランダムフォレストという名前はそれぞれの決定木が異なるモデルとなるように乱数を導入していることから命名されている。)一部のデータに対して過剰適合しているモデルでも複数集めて平均を取ることで過剰適合の度合いを減らそうというものである。
乱数の導入方法は、決定木を作るためのデータポイントを選択する方法と、特徴量を選択する方法の2種類ある。
まず、データからブートストラップサンプリング(bootstrap sample)と呼ばれる、n個あるサンプルからランダムにデータセットをn回選ぶサンプリングを行う。
(例)
サンプル [1,2,3,4]
データセット1 [2,2,3,3]
データセット2 [2,3,1,4]
次に、このデータポイントを使い決定木を作成する。この時、特徴量のサブセット([2,1]や[2,3,1]など)をランダムに選択して、その特徴量を使うものの中から最適なモデルを作成する。特徴量サブセットの大きさはmax_featuresで制御できる。上の例でいうと、max_featuresを4にすると、すべてのデータセットを使うこととなり、特徴量選択時の乱数性はなくなることに留意しよう。
cancer dataでランダムフォレストを作成してみよう。
In:
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split, cross_val_score
import numpy as np
# 3. ランダムフォレストモデルの作成
model = RandomForestClassifier(n_estimators=100, random_state=1)
# 4. モデルの訓練
model.fit(X_train, y_train)
# 5. テストデータに対する予測確率を取得
y_pred_proba = model.predict_proba(X_test)[:, 1] # クラス1(悪性)の予測確率
# 6. ROCカーブとAUCの計算
fpr, tpr, _ = roc_curve(y_test, y_pred_proba)
roc_auc = roc_auc_score(y_test, y_pred_proba) # ここでroc_auc_scoreを使用してAUCを計算することでaucを多用する際におこる定義エラーを回避
# 7. ROCカーブのプロット
plt.figure(figsize=(10, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (area = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic (ROC)')
plt.legend(loc='lower right')
plt.show()
# 8. AUCの表示
print(f'AUC: {roc_auc:.2f}')Out:

AUC=1!?!?
これは完ぺきな分類モデルであることを示す一方、過学習してしまっていてほかのデータを使ったら精度がガクんと落ちてしまう可能性を示唆している。
こんな時は交差検証を行って過学習の確認をすることが多い。第4章で詳しく話すが、交差検証とは訓練データとテストデータの分割パターンをk回繰り返しモデルをk個作ってそれぞれの精度を確認する検証方法である。
In:
# 交差検証の実施
cv_scores = cross_val_score(model, X_train, y_train, cv=5, scoring='roc_auc')
print(f'Cross-validated AUC scores: {cv_scores}')
print(f'Mean AUC: {np.mean(cv_scores):.2f}')
print(f'Standard deviation of AUC: {np.std(cv_scores):.2f}')Out:
Cross-validated AUC scores: [0.99529781 0.98529412 0.99793602 0.98323013 0.9878741 ]
Mean AUC: 0.99
Standard deviation of AUC: 0.01この結果から(SVMなどと同様)AUCが5つのモデルの平均で0.99付近であることが分かる。
また、どの特徴量が目的変数を分類するうえで重要であったかを特徴量重要度(Feature Importance)という指標で計算することができる。
計算は下記のように行う
#feature importance の確認
importances = model.feature_importances_
feature_importance_df = pd.DataFrame({'Feature': X.columns, 'Importance': importances}).sort_values(by='Importance', ascending=True)
#図示
plt.figure(figsize=(10, 6))
plt.barh(feature_importance_df['Feature'], feature_importance_df['Importance'], color='skyblue')
plt.xlabel('Importance')
plt.title('Feature Importance using Random Forest')
plt.show()2.2.5 勾配ブースティングマシン(回帰)
勾配ブースティング(Gradient Boosting)回帰木とは、ランダムフォレストと同じく決定木を使った学習法であるが、ランダムフォレストと違い、早めに事前前刈りを行うことで予測の早い浅い決定木(アンダーフィッティングという意味で弱学習機という)を使うことである。
浅い決定木を多く使うことで性能を向上させる。
ハイパーパラメータさえしっかり決めてやればこちらの方がランダムフォレストよりも精度が高くなることがある。(ランダムフォレストのほうが(乱数で作成した決定木の平均を取っているため)頑健であることが多いので、優先度的にはまずはランダムフォレストを試した方がよい)
ハイパーパラメータには、「事前枝刈り」「決定木の数」「学習率」がある。
学習率は、個々の決定木がそれまでの決定木の誤りをどれだけ補正するかを決める割合で、高ければ高いほど、モデルは複雑になる。
また、事前前刈りした決定木を大量に使うことから、計算時間は比較的長い。
In:
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib.pyplot as plt
# 3. 勾配ブースティングモデルの作成
model = GradientBoostingClassifier(n_estimators=100, learning_rate = 0.01, random_state=1)
# 4. モデルの訓練
model.fit(X_train, y_train)
# 5. テストデータに対する予測確率を取得
y_pred_proba = model.predict_proba(X_test)[:, 1] # クラス1(悪性)の予測確率
# 6. ROCカーブとAUCの計算
fpr, tpr, _ = roc_curve(y_test, y_pred_proba)
roc_auc = roc_auc_score(y_test, y_pred_proba)
# 7. ROCカーブのプロット
plt.figure(figsize=(10, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (area = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic (ROC)')
plt.legend(loc='lower right')
plt.show()
# 8. AUCの表示
print(f'AUC: {roc_auc:.2f}')Out:

・n_estimators…決定木の数を指定する
・learning_rate…学習率を指定する
2.2.6 LightGBM
この本には載っていなかったが、最近主流の決定木モデルの拡張版である、LightGBM(Light Gradient Boosting Machine)についても見ておこう。
LightGBMは2016年にMicro Soft社が公開した勾配ブースティングに基づくモデルのことである。(境界線の推理方法は勾配ブースティングと同じ)
勾配ブースティングは、事前前刈りした決定木をたくさん計算するので、処理速度が遅いというデメリットがあった。
LightGBMは
・分岐させるべき葉のみ、分岐させる
・ヒストグラムを採用し、分岐させるべき分岐点に狙いをつける
ことで処理速度を上げることで、勾配ブースティングのデメリットをなくしたモデルである。

それでは、cancerデータを予測した結果を見てみよう。
In:
import lightgbm as lgb
from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib.pyplot as plt
# 3. LightGBMモデルの作成
# 重要なパラメータとしてlearning_rate(学習率)やn_estimators(決定木の数)があります。
model = lgb.LGBMClassifier(n_estimators=100, learning_rate=0.1, random_state=1)
# 4. モデルの訓練
model.fit(X_train, y_train)
# 5. テストデータに対する予測確率を取得
y_pred_proba = model.predict_proba(X_test)[:, 1] # クラス1(悪性)の予測確率
# 6. ROCカーブとAUCの計算
fpr, tpr, _ = roc_curve(y_test, y_pred_proba)
roc_auc = roc_auc_score(y_test, y_pred_proba)
# 7. ROCカーブのプロット
plt.figure(figsize=(10, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (area = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic (ROC)')
plt.legend(loc='lower right')
plt.show()
# 8. AUCの表示
print(f'AUC: {roc_auc:.2f}')
Out:

LightGBMのハイパーパラメータは勾配ブースティング回帰木と同様に「learning_rate」「n_estimators」「max_depth」がある。
2.2.7 SVM(カーネル法を用いたサポートベクタマシン)
SVM((カーネル法を用いた)サポートベクタマシン)とは、特徴量の2乗項や3乗項などの高次元の項を入れることにより、非線形で境界線を引く方法である。
例えば、下記の図のようなデータセットに対して境界線を引くことを考えてみよう。
線形の境界線を引くことはできないことがよく分かる。


そこで、重要特徴量の項の2乗項を入れてみよう。

すると、下記のようにうまく境界線が引けることが分かる。

この境界線を2つ引くと、うまく分離できる。
2次元で見てみると、上記の境界線が曲線を描くことが分かる。

2つのクラスの境界線に最も近いデータポインタをサポートベクタ(support vector)と呼ぶ。SVMはサポートベクタと個々のデータポインタとの差を用いて境界線を引く。

重要なハイパーパラメータとして、C(コストパラメータ)とgammaがある。
Cは、誤分類をどれだけ許容するかを決めるパラメータ。値が大きいほど、誤分類を減らすために境界線の制約が厳しくなり、マージンが狭くなる。(モデルが過学習しやすくなる。)
gammaは、データポイント間の影響範囲を決めるパラメータ。値が大きいと、モデルはより詳細な境界を引き、過学習しやすくなる。
例えば、gammaを0.1、1、10で変化させた結果を示す。

gammaが小さいほど汎用的で、大きいほど個々の点を重視していることが分かる。
SVMは決定木を使っているわけではないので、各特徴量のスケールを一定にして、特徴量のスケールの違いを考慮する必要があることに留意しよう。
それでは、最後に、cancerデータセットに対してのSVMの結果を見てみよう。
In:
from sklearn.svm import SVC
from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib.pyplot as plt
# 3. SVMモデルの作成
model = SVC(kernel='linear', probabili#ty=True, random_state=1)
#model = SVC(kernel='rbf', C=1000, gamma=10.0, probability=True, random_state=1) のような形でハイパーパラメータを決定する
# 4. モデルの訓練
model.fit(X_train, y_train)
# 5. テストデータに対する予測確率を取得
y_pred_proba = model.predict_proba(X_test)[:, 1] # クラス1(悪性)の予測確率
# 6. ROCカーブとAUCの計算
fpr, tpr, _ = roc_curve(y_test, y_pred_proba)
roc_auc = roc_auc_score(y_test, y_pred_proba)
# 7. ROCカーブのプロット
plt.figure(figsize=(10, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (area = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic (ROC)')
plt.legend(loc='lower right')
plt.show()
# 8. AUCの表示
print(f'AUC: {roc_auc:.2f}')
Out:

2.2.8 ニューラルネットワーク
2.3 多クラス分類を予測するモデル
ロジスティック回帰モデルは多クラス分類モデルとしても機能する一方、決定木やランダムフォレストでは「1対多(one-vs.-rest)」の分類をする必要がある。
In:
import sklearn
print(sklearn.__version__)Out:
1.4.2第3章 教師なし学習
次に、教師なし学習についてまとめていく。
教師なし学習とは「教師データを用いない、すべての種類の機械学習」のことである。アルゴリズムには入力データだけが与えられ、出力データからは結果や知識を抽出することが求められる。
主な教師なし学習の種類は下記の通り。
・データセットの変換(e.g. 次元削減、標準化、正規化)
教師あり学習の前処理等で行われる学習の一つ。元データの簡素化や処理の高速化等のために、データの持つ特性を崩すことなく変換すること。
・クラスタリング(e.g. 画像処理)
データを似たような要素から構成されるグループに分けるアルゴリズム。
教師なし学習の難しい点としては
「アルゴリズムが学習したことの解釈方法(評価方法)」
が挙げられる。
そのため、教師なし学習の多くは、データサイエンティストがデータをより理解するために探索的に用いられることが多い。
3.1 前処理とスケール変換
それでは早速、教師なし学習の一つである「データセットの変換」(スケール変換)を考えてみよう。
スケール変換処理は、教師あり学習で、前処理として行うことが多い。
以下がその例である。
In:
import mglearn
import matplotlib.pyplot as plt
mglearn.plots.plot_scaling()
plt.show()Out:

Original DataがX軸10~15、Y軸0~10あたりを取っているのに対し、それぞれデータの持つ大きさが変化しているのが分かる。上記4種類のスケール変換処理方法について
・StandardScaler(標準化)
(x-μ)/σ
データの平均を0、標準偏差を1に変換するプロセス。これは、特徴量のスケールを揃えるためによく使用される。
・Normalizer(正規化)
x/||x||
||x||はノルムを指す。デフォルトではL2ノルム。

Normalizer は各サンプルのベクトルの長さを1にスケーリングします。これにより、各サンプルの異なる特徴量が同じスケールで表現される。
主にテキスト処理やクラスタリングの前処理として使用される。
・MinMaxScaler
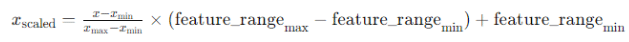
各特徴量を指定された範囲(デフォルトでは0から1)にスケーリングするために使用される。
・RobustScaler
(x−median(x))/IQR(x)
median(x)\text{median}(x)は特徴量 xx の中央値。
IQR(x)\text{IQR}(x)は特徴量 xx の四分位範囲で、具体的には75パーセンタイル値から25パーセンタイル値を引いた値。
よく使うスケール変換として標準化と正規化があるのだが、それぞれ一般的にどのような際に使用するのかがまとまったWebページを見て大まかに把握しよう。
mglearnをインポートしようとしても、環境になかったので、anaconda promptでconda install mglearn としたところ、PackagesNotFoundErrorがでた。chatgptに解決方法を聞いてみると、pip で代わりにインポートできるとのことで、試したところやはりうまくいった。私自身、pipとcondaの違いを全然理解できてないので、chatgptにきいたところ以下の回答が返ってきた。chatgpt、あんたは天才だよ。
(僕の質問)
>なぜanacondaの環境のパッケージをpipでインストールできるの?
(chatgpt様の回答)
ChatGPT
Anaconda 環境で pip を使ってパッケージをインストールできる理由は、pip と conda がどちらも Python パッケージを管理するツールであり、Anaconda 環境内で共存することが可能だからです。ただし、いくつかの注意点があります。
conda と pip の違い
パッケージ管理の方法:
conda: 主に Python に限らず、幅広いソフトウェアパッケージ(C、C++、FORTRAN など)を管理します。依存関係の解決も含めて、包括的にパッケージ管理を行います。
pip: 主に Python パッケージを管理します。PyPI(Python Package Index)からパッケージをインストールします。
インストール場所:
conda: Anaconda の環境内にパッケージをインストールします。
pip: Python の標準環境にパッケージをインストールしますが、Anaconda 環境で実行すれば、その環境内にインストールされます。
Anaconda 環境で pip を使う理由
パッケージの可用性: 一部のパッケージは conda チャンネルにはなく、pip でのみインストール可能です。mglearn はその一例です。
最新バージョン: pip では、より新しいバージョンのパッケージが提供されている場合があります。
注意点
依存関係の競合: conda と pip を混在して使うと、依存関係の競合が発生する可能性があります。このため、できるだけ同じツールを使ってパッケージを管理することが推奨されます。
環境の一貫性: 重要なプロジェクトや本番環境では、環境の一貫性を保つために、どちらか一方のツールに統一する方が安全です。
推奨手順
conda でインストール可能なパッケージ: まずは conda でインストールを試みます。
conda install パッケージ名
pip でインストール: conda で見つからない場合、pip を使います。まずは仮想環境を作成してから pip を使用すると安全です。
conda create -n myenv python=3.8 conda activate myenv pip install mglearn
これにより、Anaconda 環境内で pip を使ってパッケージをインストールすることが可能になります。依存関係の競合を避けるために、可能な限り conda と pip を混在させないように注意しましょう。
3.1.1 データ変換の適用
「2章 教師あり学習」で使用したcancerデータを用いて、データ変換の使用方法を実際に確認してみよう。
・SVCを用いて、MinMaxScalerを前処理に用いた場合。
まずはデータセットをロードし、訓練データとテストデータに分ける。
(前処理前に、訓練データとテストデータに分ける必要がある!
訓練データでのスケール変換処理方法をテストデータに当てはめるため。)
In:
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split
(cancer.data, cancer.target, random_state=1)Out:

In:
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
#MinMaxScalerをfitさせる
scaler.fit(X_train)・fitメソッドで、訓練データ中の各特徴量の最大値と最小値を計算する。
教師あり学習とは異なり、スケール変換器のfitメソッドにはy_trainは用いない。
スケーリングの対象はあくまで特徴量であり、目的変数は特徴量のスケーリングに直接関係がない。モデルの学習段階でターゲット変数をスケーリングしてしまうと、予測時にも同じスケール変換を適用する必要が発生する(これは不必要に複雑)。
通常はターゲット変数はそのままのスケールで扱う。
MinMaxScalerの結果確認
In:
X_train_scaled = scaler.transform(X_train)
print("transformed shape: {}".format(X_train_scaled.shape))
print("per-feature minimum after scaling:\n {}".format(X_train_scaled.min(axis=0)))
print("per-feature maximum after scaling:\n {}".format(X_train_scaled.max(axis=0)))Out:
transformed shape: (426, 30)
per-feature minimum after scaling:
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.]
per-feature maximum after scaling:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.]次に、テストデータについて、スケーリングする。
In:
X_test_scaled = scaler.transform(X_test)
print("per-feature minimum after scaling:\n{}".format(X_test_scaled.min(axis=0)))
print("per-feature maximum after scaling:\n{}".format(X_test_scaled.max(axis=0)))Out:
per-feature minimum after scaling:
[ 0.0336031 0.0226581 0.03144219 0.01141039 0.14128374 0.04406704
0. 0. 0.1540404 -0.00615249 -0.00137796 0.00594501
0.00430665 0.00079567 0.03919502 0.0112206 0. 0.
-0.03191387 0.00664013 0.02660975 0.05810235 0.02031974 0.00943767
0.1094235 0.02637792 0. 0. -0.00023764 -0.00182032]
per-feature maximum after scaling:
[0.9578778 0.81501522 0.95577362 0.89353128 0.81132075 1.21958701
0.87956888 0.9333996 0.93232323 1.0371347 0.42669616 0.49765736
0.44117231 0.28371044 0.48703131 0.73863671 0.76717172 0.62928585
1.33685792 0.39057253 0.89612238 0.79317697 0.84859804 0.74488793
0.9154725 1.13188961 1.07008547 0.92371134 1.20532319 1.63068851]テストデータにおいては0~1の間に収まっていない変数がいくつかある
これは、MinMaxScalerが常に、訓練データに対して行った変換の挙動を行うからである。(Python素晴らしい…)
3.1.2 訓練データとテストデータを同じように変換する
これは非常に大切なことで(私はこのことを知らず実務で大変苦い思いをした記憶がある)、訓練データとテストデータを別々にスケーリングすると、お互いのデータがばらばらに動くため、元のデータの特徴(分布)が変化してしまうのである。
下記、①訓練データのスケール変換をテストデータに当てはめた場合 ②訓練データとテストデータをバラバラにスケール変換した場合 の結果の違いである。
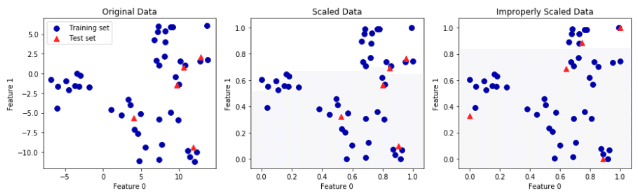
一番左がオリジナル、真ん中が①の場合、右が②の場合の散布図である。
明らかに②ではデータセットが変わってしまっていることが分かる。
【メモ】効率のいいショートカット
モデルをfitしてからtransformすることがよくあるため、下記でそれぞれを一緒に行える
fit_transform
(例)
X_scaled = scaler.fit_transform(X)
3.1.3 教師あり学習における前処理の効果
それでは、実際にSVCの学習に対するスケール変換処理の効果を見てみよう。
(※ここでは本書と異なり練習のために標準化を用いる)
まずは、スケール変換していない特徴量を用いて、SVCのテストデータの正解率を算出してみよう。
In:
#教師あり学習における前処理の効果
from sklearn.svm import SVC
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, random_state=0)
svm = SVC(C=100)
svm.fit(X_train, y_train)
print("Test set accuracy: {:.2f}".format(svm.score(X_test, y_test)))Out:
Test set accuracy: 0.94精度が0.94と、まずまずの結果となった。
次に、標準化でスケール変換した場合の正解率を見てみよう。
In:
#標準化でスケール変換する
from sklearn.preprocessing import StandardScaler
import numpy as np
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
#変換された訓練データで学習
svm.fit(X_train_scaled,y_train)
print("Scaled test set accuracy: {:.2f}".format(svm.score(X_test_scaled, y_test)))Out:
Scaled test set accuracy: 0.96正解率が96%と、先ほどより2%向上したことが分かる。
スケール変換には複雑な計算はないが、ミス削減のためにsikit-learnのパッケージを使ったほうがいいと思う。
3.2 次元削減、特徴量抽出、多様体学習
次元削減や特徴量抽出などの教師なし学習で最もよく使われるアルゴリズムは、主成分分析(principal component analysis)である。
3.2.1 主成分分析(PCA)
主成分分析とは
①特徴量の分散共分散行列の計算
②分散共分散行列を固有値固有ベクトル分解
③固有値(寄与率)の大きい方からいくつかの固有値固有ベクトルを取ってくる
ことで、データの良い要約を得ることで次元削減を行う方法である。
詳細は、下記のURLを参考。
〇(主成分分析:東京大学)https://ibis.t.u-tokyo.ac.jp/suzuki/lecture/2015/dataanalysis/L7.pdf
〇【初心者向け】主成分分析(PCA)って一体何をしているの?(理論編) #教師なし学習 - Qiita
注意点としては
訓練データの次元削減を行うことができるがその同じアルゴリズムをテストデータに当てはめられないため、教師あり学習には使えない。
3.2.2 cancerデータセットのPCAによる可視化
業務上で、機械学習を行うにあたり、特徴量が50個、100個と膨大であるのが一般的である。
そのような場合は、データを可視化することは一苦労する。例えば第一章でやったペアプロットを思い出してみて欲しいのだが、あれをcancerデータに対して行った場合、30×29/2=435個の散布図が作成されてしまうことになる。
そんな時に活躍するのが主成分分析である。
まずは、第二章で使用したcancerデータを使用し、良性、悪性ごとに、各特徴量のヒストグラムを作成してみよう。
In:
from sklearn.datasets import load_breast_cancer
import numpy as np
cancer = load_breast_cancer()
fig, axes = plt.subplots(5, 6, figsize=(20, 10))
malignant = cancer.data[cancer.target == 0]
benign = cancer.data[cancer.target == 1]
ax = axes.ravel()
for i in range(30):
_, bins = np.histogram(cancer.data[:, i], bins=50)
ax[i].hist(malignant[:, i], bins=bins, color=mglearn.cm3(0), alpha=.5)
ax[i].hist(benign[:, i], bins=bins, color=mglearn.cm3(2), alpha=.5)
ax[i].set_title(cancer.feature_names[i])
ax[i].set_yticks(())
ax[0].set_xlabel("Feature magnitude")
ax[0].set_ylabel("Frequency")
ax[0].legend(["malignant", "benign"], loc="best")
fig.tight_layout()
plt.show()
Out:

・plt.subplots(a,b)…figureを一度にまとめて返す関数。a列b行で結果を返す。返り値は、以下の二つのオブジェクトをタプルで返す。
①figオブジェクト②axesオブジェクト(特定のサブプロットのカスタマイズをする際にも使用する)
・malignant…悪性、benign…良性(ここでは悪性=0となっている。実務上は検知すべき対象を1とすることが多いので、もし悪性を検知するのなら、悪性=1と変換したほうがいい気もする。。)
・ravel()…多次元の軸の配列を一次元の配列に変換する関数。axesが、5*6配列なのを、一次元配列に変換する
・np.histogram(bins=ビン数)…2つの要素を返す。1.各ビンに含まれるデータ数 2.各ビンの境界を示す数値の配列。cancer.data[:,i]の境界を示す数値のみを返す(データ数は使用しないので、_に入れている)
・hist(データ, ビン, alpha=透明度)…ヒストグラムの描写
・ax[i].hist()…特定のサブプロットに対してヒストグラムを描写する。histの前のデータがオブジェクトとなる。
(plt.hist()にしてしまうと一つのプロットに対して重複してヒストグラムが描写されてしまう)
・ax[0]…ゼロ番目のサブプロットにのみ描写する。legend()は凡例を指定する関数。
#例:サブプロットに対する処理
import matplotlib.pyplot as plt
# 図と3つのサブプロットを作成
fig, ax = plt.subplots(2, 2)
# axは2次元の配列で、それぞれの要素がサブプロットに対応している
print(ax.shape) # (2, 2)
# サブプロットにプロットを追加などの処理を行う
# ax[0, 0].plot(...) など
#プロットは、データの視覚化を指し、1つの図全体を占めます。
#サブプロットは、1つの図内に複数のプロット領域を作成するための領域であり、複数のプロットを配置することができます。このヒストグラムからは、どの特徴量が良性と悪性を区別するのに適しているのかを考えることができる。緑と青のヒストグラムが重なっている特徴量は、良性と悪性での分布が似ているということになる。
しかし、このヒストグラムからは、個々の特徴量の相関や、それがクラス分類に与える影響まではわからない。
PCAを使用すると、何が分かるだろうか。
ここでは、2つの主成分から散布図を見ることにする。
PCAを使用する前に、特徴量をスケール変換する必要がある。ここではStandardScalerを使用する。
※PCAは特徴量間の共分散行列を計算し、固有値ベクトルを算出することで寄与度をもとに次元削減を行う。特徴量間で尺度に違いがある場合、尺度の違いに共分散の計算が引っ張られてしまうため、スケール変換する必要がある。
In:
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
# PCAを使う前にスケール変換する必要がある
scaler = StandardScaler()
scaler.fit(cancer.data)
X_scaled = scaler.transform(cancer.data)元の特徴量から、PCA関数を用い2つの主成分を保持する
from sklearn.decomposition import PCA
# 元の特徴量から2つの主成分だけを保持する
pca = PCA(n_components=2)
pca.fit(X_scaled)
#X_pcaに二次元の特徴量を返す
X_pca = pca.transform(X_scaled)
#結果の確認
print("Original shape: {}".format(str(X_scaled.shape)))
print("Reduced shape: {}".format(str(X_pca.shape)))Out:
Original shape: (569, 30)
Reduced shape: (569, 2)これで、二次元の主成分に対する散布図をプロットしてみると、
In:
plt.figure(figsize=(8, 8))
mglearn.discrete_scatter(X_pca[:, 0], X_pca[:, 1], cancer.target)
plt.legend(cancer.target_names, loc="best")
plt.gca().set_aspect("equal")
plt.xlabel("First principal component")
plt.ylabel("Second principal component")
plt.show()Out:

という結果となった。
この結果より、ある程度の線形分離が可能そうであることが考えられる。
※PCAは教師なし学習であり、2つの主成分の相関を見ているだけであることに注意しよう。
PCAの欠点として、結果の解釈が難しいことが挙げられる。
主成分はPCAの適合を行う過程でcomponents_属性に格納されるため、その結果を見てみよう。
行は重要度によってソートされており、第一主成分が一番初めにくる。
列はPCA変換する前の元の特徴量に対応している。
In:
print("PCA components:\n{}".format(pca.components_))Out:
PCA components:
[[ 0.21890244 0.10372458 0.22753729 0.22099499 0.14258969 0.23928535
0.25840048 0.26085376 0.13816696 0.06436335 0.20597878 0.01742803
0.21132592 0.20286964 0.01453145 0.17039345 0.15358979 0.1834174
0.04249842 0.10256832 0.22799663 0.10446933 0.23663968 0.22487053
0.12795256 0.21009588 0.22876753 0.25088597 0.12290456 0.13178394]
[-0.23385713 -0.05970609 -0.21518136 -0.23107671 0.18611302 0.15189161
0.06016536 -0.0347675 0.19034877 0.36657547 -0.10555215 0.08997968
-0.08945723 -0.15229263 0.20443045 0.2327159 0.19720728 0.13032156
0.183848 0.28009203 -0.21986638 -0.0454673 -0.19987843 -0.21935186
0.17230435 0.14359317 0.09796411 -0.00825724 0.14188335 0.27533947]]係数をヒートマップで見てみよう。
In:
plt.matshow(pca.components_, cmap='viridis')
plt.yticks([0, 1], ["First component", "Second component"])
plt.colorbar()
plt.xticks(range(len(cancer.feature_names)), cancer.feature_names, rotation=60, ha='left')
plt.xlabel("Feature")
plt.ylabel("Principal components")
plt.show()Out:

この結果から、第一主成分ではすべての係数がプラスであり、相関があることが分かるものの、具体的な主成分の意味を考えることは難しい。
3.2.3 特徴量抽出
PCAのもう一つの利用方法は「特徴量の抽出」である。
特徴量抽出は画像データや音声データでよく使用される。
Labeled Faces in the Wildデータセットという、有名人の顔画像で構成されたデータセットを使用して、特徴量の抽出を行ってみよう。
In:
from sklearn.datasets import fetch_lfw_people
people = fetch_lfw_people(min_faces_per_person=20, resize=0.7)
image_shape = people.images[0].shape
fig, axes = plt.subplots(2, 5, figsize=(15, 8), subplot_kw={'xticks': (), 'yticks': ()})
for target, image, ax in zip(people.target, people.images, axes.ravel()):
ax.imshow(image)
ax.set_title(people.target_names[target])
plt.show()・min_faces_per_person=20で20枚以上の画像データを保持したもののみ保持
・resize=0.7 で70%の画像サイズをリサイズ
Out:

画像は62人分、3023枚ある。
特徴量の抽出においては、各画像の数を均等にしてデータセットの偏りをなくすことが大切である。
In:
counts = np.bincount(people.target#各画像に対応する人物のラベル配列)
for i, (count, name) in enumerate(zip(counts, people.target_names)):#画像数(counts)と画像の名前(target_names)をタプルにしてそれぞれをcountとnameに格納するfor文
print("{0:25} {1:3}".format(name, count), end=' ')#nameを25文字幅でに、countを3文字幅で、末尾に3つのスペースを追加
if (i + 1) % 3 == 0:#3で割り切れるとき
print()#で改行Out:
Alejandro Toledo 39 Alvaro Uribe 35 Amelie Mauresmo 21
Andre Agassi 36 Angelina Jolie 20 Ariel Sharon 77
Arnold Schwarzenegger 42 Atal Bihari Vajpayee 24 Bill Clinton 29
Carlos Menem 21 Colin Powell 236 David Beckham 31
Donald Rumsfeld 121 George Robertson 22 George W Bush 530
Gerhard Schroeder 109 Gloria Macapagal Arroyo 44 Gray Davis 26
Guillermo Coria 30 Hamid Karzai 22 Hans Blix 39
Hugo Chavez 71 Igor Ivanov 20 Jack Straw 28
Jacques Chirac 52 Jean Chretien 55 Jennifer Aniston 21
Jennifer Capriati 42 Jennifer Lopez 21 Jeremy Greenstock 24
Jiang Zemin 20 John Ashcroft 53 John Negroponte 31
Jose Maria Aznar 23 Juan Carlos Ferrero 28 Junichiro Koizumi 60
Kofi Annan 32 Laura Bush 41 Lindsay Davenport 22
Lleyton Hewitt 41 Luiz Inacio Lula da Silva 48 Mahmoud Abbas 29
Megawati Sukarnoputri 33 Michael Bloomberg 20 Naomi Watts 22
Nestor Kirchner 37 Paul Bremer 20 Pete Sampras 22
Recep Tayyip Erdogan 30 Ricardo Lagos 27 Roh Moo-hyun 32
Rudolph Giuliani 26 Saddam Hussein 23 Serena Williams 52
Silvio Berlusconi 33 Tiger Woods 23 Tom Daschle 25
Tom Ridge 33 Tony Blair 144 Vicente Fox 32
Vladimir Putin 49 Winona Ryder 24 ブッシュの画像数が530と圧倒的に多い。偏りを減らすために、各人の画像を50枚にする。
In:
#各人の画像を50枚に制限する。
mask = np.zeros(people.target.shape, dtype=bool)
for target in np.unique(people.target):
mask[np.where(people.target == target)[0][:50]] = 1
X_people = people.data[mask]
y_people = people.target[mask]
# 完全な白黒画像にする
X_people = X_people / 255.これで各人の画像数が50枚になった。
画像データの処理としてよくあることが、画像の識別(クラス分類)である。データベースの中の画像と一致するかどうかを判別するタスクである。
例として、k-最近傍法を用い、画像データのクラス分類を行ってみよう。
k=1として、一つのデータポイントからの近い画像を当てはめてみる。
In:
#最近傍法で画像の分類をしてみる(一番近い顔を探してみる)
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_people, y_people, stratify=y_people, random_state=0)
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train, y_train)
print("Test set score of 1-nn: {:.2f}".format(knn.score(X_test, y_test)))Out:
Test set score of 1-nn: 0.22精度は22%であった。これは、62クラスある中から行っていることを考えるとまずまずの結果である。
それでは、PCAを使って特徴量の抽出を行い、精度の比較をしてみよう。
ここでは、PCAのwhite optionを使用している。
【メモ】white optionとは
white optionとは、PCAによって射影された後のデータをさらに、正規化(whitening)することである。
具体的な処理は、
PCAで得られた主成分ごとの分散を計算
各成分をその分散の平方根で割る。
メリットはスケールの均一化を図れることで、デメリットは重要な主成分とそうでない主成分の区別がなくなることである。

詳細は下記参照
PCAオブジェクトを訓練し最初の100成分を算出し、訓練データとテストデータを変換する。
In:
pca = PCA(n_components=100, whiten=True, random_state=0).fit(X_train)
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
print("X_train_pca.shape: {}".format(X_train_pca.shape))#100個の主成分(特徴量)を持っていることが分かるOut:
X_train_pca.shape: (1547, 100)この主成分で1-最近傍法を行うと
In:
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train_pca, y_train)
print("Test set accuracy: {:.2f}".format(knn.score(X_test_pca, y_test)))Out:
Test set accuracy: 0.3022%⇒30%に精度が向上したことが分かる。
算出した主成分で画像データを表してみると
In:
fig, axes = plt.subplots(3, 5, figsize=(15, 12),
subplot_kw={'xticks': (), 'yticks': ()})
for i, (component, ax) in enumerate(zip(pca.components_, axes.ravel())):
ax.imshow(component.reshape(image_shape),
cmap='viridis')
ax.set_title("{}. component".format((i + 1)))
plt.show()Out:

主成分である程度の画像の特徴をとらえられていることがよくわかる。
これらの顔画像がその側面をとらえているのかは不明だが、いくつかを推測することはできる。
例えば、最初の主成分は、顔と背景のコントラストが一つの大きな側面であることが分かる。
アルゴリズムがデータを解釈する方法は人間とは全く異なる点には留意が必要である。
また、主成分の要素を増やせば増やすことで、画像の識別力が上がることも確認しておこう。
In:
mglearn.plots.plot_pca_faces(X_train, X_test, image_shape)
plt.show()Out:
3.2.4 非負値行列因子分解(NMF)
特徴量抽出の一つの方法として、非負値行列因子分解(Non-negative matrix factorization)が挙げられている。
NMFは名の通り、行列を非負の行列の積に分解する手法であり、手法元データが非負である画像データや音声データ、文字データに適用されることが多い。
具体的には、元の行列 V を、2つの非負の行列 W と H の積に分解する。数式で表すと
V≈WH
ここで、行列 V は m×n の非負の行列であり、行列 W は m×r の非負の行列、行列 H は r×n の非負の行列。
r…分解のランクまたは次元
詳細は下記ご参照。
https://www.kecl.ntt.co.jp/icl/signal/sawada/mypaper/829-833_9_02.pdf
それでは、早速NMFを顔画像データに当てはめてみよう。
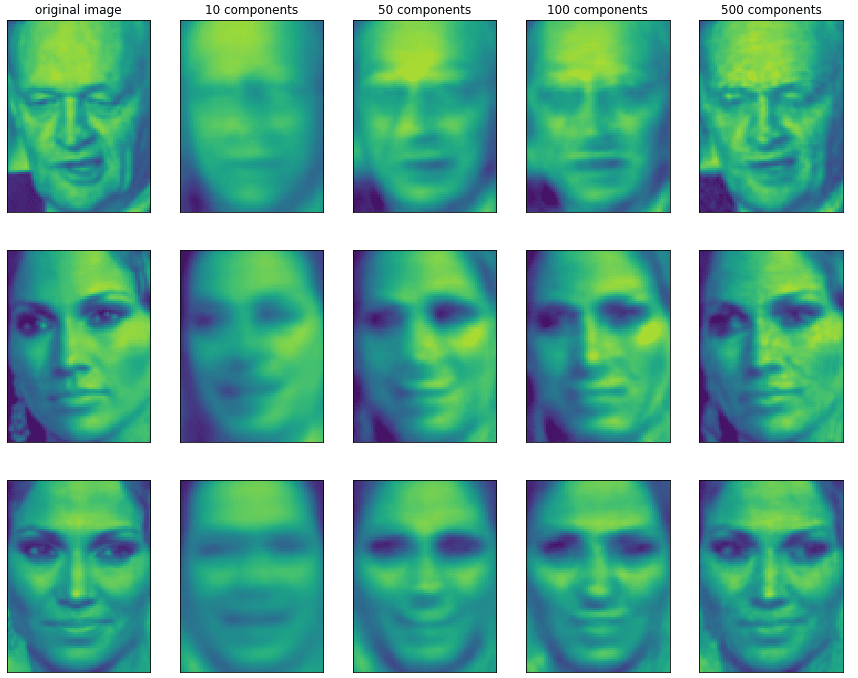
NMFでは、いくつの成分を抽出するかを指定する。10,50,100,500個の成分を抽出したときの顔画像データの再現率を確認しよう。
In:
mglearn.plots.plot_pca_faces(X_train, X_test, image_shape)
plt.show()Out:

この結果だけ見ると、500個の特徴量を抽出すれば、なんとなく元画像データを判断できそうである。
3.2.5 t-SNE
データの可視化によく用いられるアルゴリズムとして、多様体学習アルゴリズム(manifold learning algorithms)が紹介されている。t-SNEはその中の一つのアルゴリズムである。
MLAはこれまで勉強してきたPCAやNMFなどで行った、高次元データを低次元に変換するアルゴリズムである。これらのアルゴリズムは、データが埋め込まれている低次元多様体(manifold)を発見することを目指す。
多様体学習アルゴリズムは、探索的なデータの確認等には有効だが、教師あり学習には使えないことについては留意する必要がある(訓練データの次元削減をテストデータに当てはめられないため)。
t-SNEの簡単なフロー
1.データ点との距離を用いて条件付き確率を計算。データ点間の類似度を確率として表現する。
2.低次元空間でも同様に、データ点間の距離に基づいて確率分布を定義する。
3.高次元空間での確率分布 と低次元空間での確率分布 との間のコスト関数(Kullback-Leiblerダイバージェンス)を最小化する。
詳細は下記ご参照
それでは、早速t-SNEを行ってみよう。
データは、0~9までの手書きの数字の画像データセットを使用する。
In:
from sklearn.datasets import load_digits
digits = load_digits()
fig, axes = plt.subplots(2, 5, figsize=(10, 5), subplot_kw={'xticks':(), 'yticks': ()})
for ax, img in zip(axes.ravel(), digits.images):
ax.imshow(img)
plt.show()Out:

まず、比較のためにPCAを使用してこのデータを二次元にして可視化する。ここでは、どのクラスがどこにあるのかを示すために各点をその数字で表している。
In:
pca = PCA(n_components=2)
pca.fit(digits.data)
digits_pca = pca.transform(digits.data)
colors = ["#476A2A", "#7851B8", "#BD3430", "#4A2D4E", "#875525",
"#A83683", "#4E655E", "#853541", "#3A3120", "#535D8E"]
plt.figure(figsize=(10, 10))
plt.xlim(digits_pca[:, 0].min(), digits_pca[:, 0].max())
plt.ylim(digits_pca[:, 1].min(), digits_pca[:, 1].max())
for i in range(len(digits.data)):
plt.text(digits_pca[i, 0], digits_pca[i, 1], str(digits.target[i]),
color = colors[digits.target[i]],
fontdict={'weight': 'bold', 'size': 9})
plt.xlabel("First principal component")
plt.ylabel("Second principal component")
plt.show()Out:

PCAでは、数字同士で重なり合っている主成分が多く、うまく元データを区別できていないことが分かる。
次に同様のデータセットにt-SNEを使ってみよう。
In:
from sklearn.manifold import TSNE
tsne = TSNE(random_state=42)
digits_tsne = tsne.fit_transform(digits.data)
plt.figure(figsize=(10, 10))
plt.xlim(digits_tsne[:, 0].min(), digits_tsne[:, 0].max() + 1)
plt.ylim(digits_tsne[:, 1].min(), digits_tsne[:, 1].max() + 1)
for i in range(len(digits.data)):
plt.text(digits_tsne[i, 0], digits_tsne[i, 1], str(digits.target[i]),
color = colors[digits.target[i]],
fontdict={'weight': 'bold', 'size': 9})
plt.xlabel("t-SNE feature 0")
plt.xlabel("t-SNE feature 1")
plt.show()Out:

すべての数字画像データがうまく識別できていることが分かる。チューニングパラメータはデフォルトを使用すればだいたいはうまくいくらしい。
【メモ:chatGPTに聞いたt-SNEの特徴(PCAとの使い分けについて)】
非線形次元削減: t-SNEは非線形変換を用いて、データの局所的な類似性を保ちながら低次元空間に埋め込みます。
高い計算コスト: 計算が複雑で、特に大規模なデータセットに対しては時間がかかることがあります。
局所構造の保持: データの局所的な類似性を重視するため、クラスタ構造を視覚化するのに適しています。
適用例
データの可視化: 特にデータのクラスタリング構造やパターンを視覚的に理解するために使われます。
高次元データの探索: クラスターや異常検知の視覚的検証に役立ちます。
生物情報学や画像処理: 高次元データ(遺伝子発現データや画像特徴量など)のパターン認識に利用されます。
3.3 クラスタリング
クラスタリングとは、データセットを「クラスタ」と呼ばれるグループに分類する手法。
この章では3つのクラスタリングの手法が紹介されている。
k-meansクラスタリング
凝集型クラスタリング
DBSCAN
簡単に紹介すると、
〇k-meansクラスタリング
k個のクラスタを振り、各クラスタの重心を計算し、重心からのデータの距離で、各データをクラスタに割り振るクラスタリングの手法である。
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
# データセットの作成
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
# k-meansクラスタリングの適用
kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)
# クラスタの中心
centers = kmeans.cluster_centers_
# クラスタリング結果のプロット
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.75)
plt.title('K-means Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()
赤い×はそれぞれのクラスタの重心を示している
〇凝集型クラスタリング
特徴の似た者同士を凝集してクラスタリングする方法。凝集する方法はいくつか存在する。
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import AgglomerativeClustering
# データセットの作成
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
# 凝集型クラスタリングの適用
agg_clustering = AgglomerativeClustering(n_clusters=4)
y_agg = agg_clustering.fit_predict(X)
# クラスタリング結果のプロット
plt.scatter(X[:, 0], X[:, 1], c=y_agg, s=50, cmap='viridis')
plt.title('Agglomerative Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()
# デンドログラムのプロット
plt.figure(figsize=(10, 7))
dendrogram(Z)
plt.title('Dendrogram for Agglomerative Clustering')
plt.xlabel('Sample index')
plt.ylabel('Distance')
plt.show()
凝集された結果4つのクラスタになっている

〇DBSCAN(Density-Based Spatial Clustering of Applications with Noise)
密度に準拠したクラスタリング手法。密度が高いところを一つのクラスタとするため、特異なデータに対しても当てはまりやすい。
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import DBSCAN
# データセットの作成
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
# DBSCANの適用
dbscan = DBSCAN(eps=0.5, min_samples=5)
# eps... 近傍の半径。この円内の点をカウントする。
# min_samples ... eps半径内に含まれる点の数がこの値以上であれば、その点をコア点として認識する。
# コア点に接続される点も同じクラスタに属すが、eps内にmin_samples未満の点しかない点はノイズとされる。
y_dbscan = dbscan.fit_predict(X)
# クラスタリング結果のプロット
plt.scatter(X[:, 0], X[:, 1], c=y_dbscan, s=50, cmap='viridis')
plt.title('DBSCAN Clustering with viridis cmap')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()
紫色のポイントは外れ値(ノイズ)としてクラスタには属していない
それぞれのクラスタリングの具体的な方法については、本書を読んで勉強してほしい。
ロジックについては下記をご参照。
それぞれの利点と欠点についてchatGPTにまとめてもらった。
k-meansクラスタリングの利点と欠点
利点
シンプルで高速: 実装が簡単で、比較的高速に動作します。
拡張性: 大量のデータにも対応できます。
欠点
初期値の依存性: 初期のセントロイドの選び方によって、結果が異なる場合があります。
球形クラスタ: クラスタが球形で均一なサイズの場合に最も効果的です。異なる形状やサイズのクラスタには適さないことがあります。
クラスタ数の事前指定: 適切なクラスタ数 k を事前に決定する必要があります。
凝集型クラスタリングの利点と欠点
利点
階層的構造:
デンドログラム(樹状図)を生成するため、クラスタの階層的な関係を視覚的に確認できます。
データの階層的な構造を理解するのに役立ちます。
クラスタ数の事前指定不要:
k-meansとは異なり、事前にクラスタ数を指定する必要がありません。最終的なクラスタ数はデンドログラムを切る位置によって決定されます。
様々な距離尺度:
ユークリッド距離、マンハッタン距離、コサイン類似度など、さまざまな距離尺度を使ってクラスタリングを行うことができます。
ノイズに強い:
単一のアウトライアによる影響が比較的小さいため、ノイズや外れ値に対して比較的ロバストです。
欠点
計算コストが高い:
特に大規模データセットに対しては、計算量が O(n3) となるため、計算時間が長くなります。
データポイントが増えると、メモリ使用量も大きくなります。
固定された階層構造:
一度マージしたクラスタは分割されないため、初期の結合ミスが最終結果に大きな影響を与える可能性があります。
クラスタ形状に依存しない:
任意の形状のクラスタを見つけることができますが、クラスタのサイズや密度に敏感であるため、異なる密度のクラスタを扱うのが難しい場合があります。
解釈の難しさ:
デンドログラムが複雑になると、解釈が難しくなる場合があります。
DBSCANの利点と欠点
利点
クラスタ数の事前指定不要:
クラスタ数を事前に指定する必要がありません。クラスタはデータの密度に基づいて自動的に決定されます。
任意の形状のクラスタ:
球形に限らず、任意の形状のクラスタを検出することができます。密度が異なるクラスタも適切に処理できます。
ノイズと外れ値の検出:
ノイズや外れ値を自動的に識別し、クラスタに含めません。これにより、クラスタリング結果が外れ値の影響を受けにくくなります。
クラスタの不均一性に対応:
密度が異なるクラスタを適切に処理できるため、クラスタのサイズや密度が不均一な場合にも有効です。
欠点
パラメータの選定が難しい:
ε\varepsilonε(epsilon)と最小ポイント数(minPts)という2つのパラメータを適切に設定する必要があります。これらのパラメータを適切に選定するのは、データセットによっては難しい場合があります。
高次元データでの性能低下:
高次元データでは、距離の概念が曖昧になるため、DBSCANの性能が低下することがあります。高次元データに対しては、適切な距離尺度や次元削減手法を検討する必要があります。
密度の変化に敏感:
同一のデータセット内で密度が大きく異なる領域が存在する場合、適切なパラメータの選定がさらに難しくなります。このような場合、一部のクラスタが正しく検出されない可能性があります。
計算コスト:
特に大規模データセットに対しては、DBSCANの計算コストが高くなる場合があります。データポイント間の距離計算が多く必要となるため、計算時間が長くなることがあります。
DBSCANは、クラスタの形状やサイズが不均一なデータセットに対して非常に有効な手法です。しかし、パラメータ設定の難しさや高次元データでの性能低下といった欠点も考慮する必要があります。適切なパラメータ選定を行うために、データの事前分析や試行錯誤が求められることが多いです。
3.4 クラスタリングの評価
正解データとの比較や異なるクラスタリングアルゴリズムの結果の比較を行う際に、調整ランド指数(adjusted rand index: ARI)や正規化相互情報量(normalized mutual information: NMI)などが使われる。
それぞれ0~1の値をとり、最良の場合に1を、関係のないクラスタリングの場合0をとる。
クラスタリングの評価でaccuracy_scoreを使っても何も意味がないことには留意すべきだ。
accuracy_scoreはそれぞれのクラスタラベルの整合性を図るが、クラスタラベル自体には何も意味がないからである。
以下は、scikit-learnのデータセットを使用し、k-meansクラスタリングを行った後にARIを計算する例です。
In:
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import adjusted_rand_score
# サンプルデータの生成
X, true_labels = make_blobs(n_samples=100, centers=3, cluster_std=0.60, random_state=0)
# k-meansクラスタリングの適用
kmeans = KMeans(n_clusters=3)
kmeans.fit(X)
predicted_labels = kmeans.labels_
# Adjusted Rand Indexの計算
ari = adjusted_rand_score(true_labels, predicted_labels)
print("Adjusted Rand Index: {:.3f}".format(ari))Out:
Adjusted Rand Index: 0.940make_blobs は、scikit-learn ライブラリに含まれている関数で、クラスタリングアルゴリズムのテストやデモンストレーションのための合成データセットを生成するために使用される。n_samples: 生成するデータポイントの総数。デフォルトは100。centers: 生成するクラスタの数。整数または配列で指定します。整数の場合、その数のクラスタを生成します。配列の場合、クラスタの中心を指定します。cluster_std: 各クラスタの標準偏差。デフォルトは1.0。
adjusted_rand_score(true_labels, predicted_labels) でtrue_labelとpredict_labelのARIを計算している。
3.5 顔画像データでクラスタリング手法を確認してみよう
3.5.1 DBSCAN
最初はDBSCANによる解析を行ってみよう。
In:
from sklearn.decomposition import PCA
pca = PCA(n_components=100, whiten=True, random_state=0)
pca.fit_transform(X_people)
X_pca = pca.transform(X_people)
#DBSCANを適用
dbscan = DBSCAN()
labels = dbscan.fit_predict(X_pca)
print("Unique labels: {}".format(np.unique(labels)))Out:
Unique labels: [-1]すべてのラベルが-1となっており、「ノイズ」と判断されている。
min_samples = 1 とし、より小さいクラスタで識別してみると(デフォルトでは5)
In:
dbscan = DBSCAN(min_samples=1, eps=15)
labels = dbscan.fit_predict(X_pca)
print("Unique labels: {}".format(np.unique(labels)))Out:
Unique labels: [-1]epsを大きくして個々の点の近傍を拡大してみると
In:
dbscan = DBSCAN(min_samples=3, eps=15)
labels = dbscan.fit_predict(X_pca)
print("Unique labels: {}".format(np.unique(labels)))Out:
Unique labels: [-1 0]となった。
ノイズとなった画像を確認してみる。
このような、外れ値を検出する解析を外れ値検出(outlier detection)と呼ぶ。
In:
noise = X_people[labels==-1]
fig, axes = plt.subplots(3, 9, subplot_kw={'xticks': (), 'yticks': ()},
figsize=(12, 4))
for image, ax in zip(noise, axes.ravel()):
ax.imshow(image.reshape(image_shape), vmin=0, vmax=1, cmap='gray')
plt.show()Out:

outlier detectionの結果、顔が近すぎる画像、グラスや帽子が映り込んでいる画像がノイズ(外れ値)となっていることが分かる。
eps = 7 の結果からクラスタリングされた13個のクラスタに属した顔画像を確認してみよう。
In:
dbscan = DBSCAN(min_samples=3, eps=7)
labels = dbscan.fit_predict(X_pca)
for cluster in range(max(labels) + 1):
mask = labels == cluster
n_images = np.sum(mask)
fig, axes = plt.subplots(1, n_images, figsize=(n_images * 1.5, 4),
subplot_kw={'xticks': (), 'yticks': ()})
for image, label, ax in zip(X_people[mask], y_people[mask], axes):
ax.imshow(image.reshape(image_shape), vmin=0, vmax=1, cmap='gray')
ax.set_title(people.target_names[label].split()[-1])
plt.show()Out:

個々のクラスタ内で顔の向きや表情などが一致していることが分かる。また、小泉元総理については、ある程度識別できていることも分かる。
3.5.2 k-meansと凝集型クラスタリング
次に、k-meansと凝集型クラスタリングによる結果について確認してみよう。これらは、DBSCANと異なり、自身でクラスタリング数を指定できるので、それぞれ10個で
In:
# k-Means
km = KMeans(n_clusters=10, random_state=0)
labels_km = km.fit_predict(X_pca)
print("Cluster sizes k-means: {}".format(np.bincount(labels_km)))
# 凝集型クラスタリング
agglomerative = AgglomerativeClustering(n_clusters=10)
labels_agg = agglomerative.fit_predict(X_pca)
print("cluster sizes agglomerative clustering: {}".format(np.bincount(labels_agg)))Out:
Cluster sizes k-means: [ 78 179 179 189 235 355 286 252 139 171]
cluster sizes agglomerative clustering: [560 108 168 281 133 200 44 52 445 72]k-meansの場合は、最小で26画像、最大で623画像がクラスタリングされている。
凝集型クラスタリングの場合は、最小で26画像、最大で623画像がクラスタリングされている。
k-meansと凝集型クラスタリングの分割の結果を比較すると、
In:
print("ARI: {:.2f}".format(adjusted_rand_score(labels_agg, labels_km)))Out:
ARI: 0.09ARIが0.09であり、二つのクラスタリングに全然共通点がないことが分かる。
どちらかのクラスタリングを優先したほうがよさそうである。
次に凝集型クラスタリングの場合のデンドログラムを描写してみよう。
In:
linkage_array = ward(X_pca)
plt.figure(figsize=(20, 5))
dendrogram(linkage_array, p=7, truncate_mode='level', no_labels=True)
plt.xlabel("Sample index")
plt.ylabel("Cluster distance")
plt.show()Out:

10クラスタを作るのは、木構造のかなり上のほうで切り取ることになっていることが分かる。2~3クラスでデータの性質をとらえられていることが分かる。
デンドログラムの詳しい見方についてはchatGPTに聞いてみた。
デンドログラム(dendrogram)は、階層的クラスタリングの結果を視覚的に表現するためのツールです。データポイントがどのようにグループ化されていくかを示し、クラスタの階層的な関係を理解するのに役立ちます。以下に、デンドログラムの詳しい見方と解釈方法を説明します。
デンドログラムの構成要素
リーフ(葉): デンドログラムの一番下に位置する部分で、各データポイントを表します。
ブランチ(枝): データポイントやクラスタ間の距離を示す線です。ブランチの長さは、クラスタ間の距離を表しています。
ノード(結節): データポイントやクラスタが統合される点を示します。
デンドログラムの見方
クラスタの統合順序:
デンドログラムは下から上に向かって構築されます。リーフからスタートし、ペアごとに結合していきます。結合が進むにつれて、より高いレベルでクラスタが統合されます。
クラスタ間の距離:
ノードの位置(縦軸の高さ)は、クラスタ間の距離を示します。ノードが高い位置にあるほど、そのクラスタ間の距離が大きいことを意味します。
クラスタの数:
デンドログラムを横に切ることで、任意のクラスタ数を決定できます。切る高さによって、異なる数のクラスタが得られます。
クラスタの数を40に設定し、いくつかの結果を見てみよう。
In:
agglomerative = AgglomerativeClustering(n_clusters=40)
labels_agg = agglomerative.fit_predict(X_pca)
print("cluster sizes agglomerative clustering: {}".format(np.bincount(labels_agg)))
n_clusters = 40
for cluster in [10, 13, 19, 22, 36]:
mask = labels_agg == cluster
fig, axes = plt.subplots(1, 15, subplot_kw={'xticks': (), 'yticks': ()},
figsize=(15, 8))
cluster_size = np.sum(mask)
axes[0].set_ylabel("#{}: {}".format(cluster, cluster_size))
for image, label, asdf, ax in zip(X_people[mask], y_people[mask],
labels_agg[mask], axes):
ax.imshow(image.reshape(image_shape), vmin=0, vmax=1, cmap='gray')
ax.set_title(people.target_names[label].split()[-1],
fontdict={'fontsize': 9})
for i in range(cluster_size, 15):
axes[i].set_visible(False)
plt.show()Out:
cluster sizes agglomerative clustering: [ 77 24 115 99 157 43 127 58 69 67 100 40 19 264 19 66 45 18
48 52 66 27 13 27 36 25 4 9 17 4 6 47 2 1 54 10
49 117 4 38]
こうしてみると、笑っている顔、怒っている顔、メガネをかけている顔、見ている方向などでクラスタリングされていることがわかる。
3.6 クラスタリングまとめ
このように、クラスタリングには様々な方法がある一方、その結果については教師あり学習のaccuracy scoreのように、わかりやすい精度の確認方法がないのが現状である。
そのため、本書のように、まずはデータセットの特徴をとらえ(直線的にクラスタリングできるものかそうでないのかを主成分分析で確認したりして)それにフィットしそうなアルゴリズムを2~3個当てはめてみて、最後にクラスタリングされた画像を目で確認する方法がよいと思う。
第4章 特徴量エンジニアリング
第4章では、特徴量エンジニアリングについての説明があった。
この章も非常にためになることが記載されているのだが、実務と乖離している箇所も多々あったので、私なりに大切なことだけをまとめようと思う。
4.1 特徴量の変換
特徴量エンジニアリングとは
特定のアルゴリズムに対して、最良のデータ表現を模索すること
その中でも最たる例として、特徴量を変換することが挙げられる。
特徴量(データ)には、大きく3つの種類がある。
連続データ…数値。任意の範囲内で無限に多くの値を取るデータ。線形で書かれる。(例:気温、長さ、重さ、時間)
離散データ…数値。任意の範囲内で有限個の値を取るデータ。点で書かれる。(例:カウント数、サイコロの目)
カテゴリカルデータ…カテゴリー。ラベル順には意味がないので、扱う際は注意が必要。(例:血液型、種類、性別)
それぞれの特徴量にはそれぞれの変換方法が存在する。
例えば、連続データであれば、標準化や正規化をこれまでで勉強してきた。
そのほかには以下のような方法が挙げられる。
4.1.1 ダミー変数(one-hot coding)
ダミー変数とは、カテゴリカルデータを0、1の2値(数値)で示すことである。
ダミー変数の扱いやすい点は、
1.カテゴリーを数値データとして処理できる
2.ダミー変数に対する回帰係数の解釈が直観的である
ダミー変数を作成する例として、色と服のサイズをダミー変数として作成する方法を見てみよう。
In:
import pandas as pd
# サンプルデータの作成(color、size)
data = {
'color': ['red', 'blue', 'green', 'blue', 'red'],
'size': ['S', 'M', 'L', 'M', 'S']
}
# データフレームの作成
df = pd.DataFrame(data)
# ダミー変数の作成
df_dummy = pd.get_dummies(df, columns=['color', 'size'])
# 結果の表示
print(df_dummy)Out:
color_blue color_green color_red size_L size_M size_S
0 0 0 1 0 0 1
1 1 0 0 0 1 0
2 0 1 0 1 0 0
3 1 0 0 0 1 0
4 0 0 1 0 0 1色(青、緑、赤)とサイズ(L、M、S)に対し、pd.get_dummies()でダミー変数を作成できる。
オプションとして、
drop_first=True でk-1個のダミー変数が作成される。
ダミー変数の作成に関する詳細は下記ご参照。
4.1.2 ビニング
ビニングとは、連続データに対して、ビンを作ってその中の特徴量をカテゴライズする方法である。
連続データの場合、線形回帰では当てはまりが悪い場合がある。また、外れ値があった場合はその値に影響を受けやすい。
そういった場合にビニングをするとどうなるのか見てみよう。
まずは、非線形なデータセットを作成してみよう
In:
# サンプルデータの作成
np.random.seed(0)
X = np.random.rand(100, 1) * 10 # 0から10の間のランダムな数値
y = 2 * np.sin(X).ravel() + np.random.randn(100) * 0.5 # 非線形な関係
# データの可視化
plt.scatter(X, y, color='blue')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Original Data')
plt.show()Out:

このデータに直線を当てはめてみても、当てはまりが非常に悪いことが分かる。
In:
# 線形回帰モデルの訓練(ビニング処理前)
model = LinearRegression()
model.fit(X, y)
y_pred = model.predict(X)
# 結果の可視化
plt.scatter(X, y, color='blue', label='Original data')
plt.plot(X, y_pred, color='red', label='Linear fit')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Linear Regression Fit (Before Binning)')
plt.legend()
plt.show()
# 平均二乗誤差の計算
mse_before = mean_squared_error(y, y_pred)
print(f'Mean Squared Error (Before Binning): {mse_before}')Out:
Mean Squared Error (Before Binning): 1.80
ビニング処理をしてみると
In:
# ビニング処理
binning = KBinsDiscretizer(n_bins=5, encode='onehot-dense', strategy='uniform')
X_binned = binning.fit_transform(X)
# ダミー変数のデータフレーム化
df_binned = pd.DataFrame(X_binned, columns=[f'bin_{i}' for i in range(X_binned.shape[1])])
# 結果の表示
print(df_binned.head())Out:
bin_0 bin_1 bin_2 bin_3 bin_4
0 0.0 0.0 1.0 0.0 0.0
1 0.0 0.0 0.0 1.0 0.0
2 0.0 0.0 0.0 1.0 0.0
3 0.0 0.0 1.0 0.0 0.0
4 0.0 0.0 1.0 0.0 0.0In:
# 線形回帰モデルの訓練(ビニング処理後)
model_binned = LinearRegression()
model_binned.fit(X_binned, y)
y_pred_binned = model_binned.predict(X_binned)
# 結果の可視化
plt.scatter(X, y, color='blue', label='Original data')
plt.scatter(X, y_pred_binned, color='red', label='Binned fit')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Linear Regression Fit (After Binning)')
plt.legend()
plt.show()
# 平均二乗誤差の計算
mse_after = mean_squared_error(y, y_pred_binned)
print(f'Mean Squared Error (After Binning): {mse_after}')Out:
Mean Squared Error (After Binning): 0.75
ビニング処理は、新たな変数を作成するときなどにも使用する。
連続データに対してビニング処理を行う方法としては、cut関数とqcut関数がある。cut関数とqcut関数の使い方については下記の通り。
4.1.2.1 cut関数
cut関数は指定されたビンの境界線に基づいてデータを分割する。
等間隔のビンを作成したいときに使用する。
(基本的には、連続データの変数に対して「自身で境界線を指定する」以外は、cut関数で(等間隔で)ビニングしたほうがいいと思う。)
使用例
In:
data = [1, 7, 5, 4, 6, 9, 3, 2]
bins = [0, 3, 6, 9]
categories = pd.cut(data, bins, labels = ['<0<=3', '<3<=6', '<6<=9'])
print(categories)Out:
['<0<=3', '<6<=9', '<3<=6', '<3<=6', '<3<=6', '<6<=9', '<0<=3', '<0<=3']
Categories (3, object): ['<0<=3' < '<3<=6' < '<6<=9']引数
data … ビニング対象の配列やseries。
bins … ビンの境界線を指定するリスト。左が開区間で右が閉区間(左端は含まれず右端は含まれる)。
labels … 各ビンに対応するラベル。
right … ビンの右側を閉じるかどうかを指定するbool値。デフォルトではright=True
注意
デフォルトでは左が開区間となっている。
ビンに当てはまらない値はNanとなってしまうため、fillna関数によるNan
への定義が必要となる。
4.1.2.2 qcut関数
qcut関数はデータを指定されたビンの数に等しくビニングする。そのため、各ビンにはほぼ同じ数のデータポイントが含まれる。
(ビニングのされかたによっては、同じ値でも異なるビンにビニングされることがあるためあまり使用しない。)
使用例
In:
data = [1, 7, 5, 4, 6, 9, 3, 2]
categories = pd.qcut(data, 3)
print(categories)Out:
[(0.999, 3.333], (5.667, 9.0], (3.333, 5.667], (3.333, 5.667], (5.667, 9.0], (5.667, 9.0], (0.999, 3.333], (0.999, 3.333]]
Categories (3, interval[float64, right]): [(0.999, 3.333] < (3.333, 5.667] < (5.667, 9.0]]引数
data … ビニング対象の配列やseries。
q … ビンの数(分位数のリスト)
labels … 各ビンに対応するラベル。
注意
ビニングのされかたによっては、同じ値でも異なるビンにビニングされる
4.1.3 指標スコア、黒データ割合(目的変数を特徴量として使用する方法)
線形回帰を行うとき、特徴量をそのまま使用すると当てはまりの悪さから、精度が思うように出ない時がある。
そのようなとき、特徴量をビニングやダミー変数等で変形し、線形回帰に対する当てはまりをよくすることが多い。
特に、二値予測モデルで有効な変形方法の一つが「指標スコア」と呼ばれるものである。
二値予測モデルは、黒データ(当てる対象のデータポイント)を予測するモデルである。(例:異常検知、不正検知など)
指標スコアは、目的変数を使用してビニングすることで、目的変数に連動した(ある意味カンニングのような)変数のエンジニアリング方法である。
作り方
ビンの数を考える(性別などのカテゴリデータに対しては必要なし)
ビンの中の黒データ、白データの割合を計算する
黒データ割合を白データ割合で割り対数をとる
数式で書くと
指標スコア=ln(ビンの黒データ割合/ビンの白データ割合)
となる。
例として、年齢の指標スコアを考えてみよう。
まず、年齢データのヒストグラムを確認して任意の範囲でビニングする。
In:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 1. データの準備
np.random.seed(42)
age_data = np.random.randint(18, 80, size=1000)
# 黒データ・白データのラベルをランダムに割り当てる(例: 0=白データ, 1=黒データ)
labels_data = np.random.choice([0, 1], size=1000, p=[0.7, 0.3])
# データフレームの作成
df = pd.DataFrame({'age': age_data, 'label': labels_data})
# 2. ヒストグラムの表示
plt.hist(df['age'], bins=20, edgecolor='k', alpha=0.7)
plt.title('Age Distribution')
plt.xlabel('Age')
plt.ylabel('Frequency')
plt.show()Out:

それぞれのビンに対する黒データの割合を計算する。
In:
# 3. ビニングの実施
bins = [0, 20, 30, 40, 50, 60, 70, 80, 100]
bin_labels = ['0-20', '21-30', '31-40', '41-50', '51-60', '61-70', '71-80', '81+']
df['age_bin'] = pd.cut(df['age'], bins=bins, labels=bin_labels, right=False)
# 4. 各ビン内の黒データと白データの割合を計算
# クロス集計を作成
bin_counts = df.groupby(['age_bin', 'label']).size().unstack(fill_value=0)
# 黒データと白データの割合を計算
bin_counts['total'] = bin_counts[0] + bin_counts[1]
bin_counts['white_ratio'] = bin_counts[0] / bin_counts['total']
bin_counts['black_ratio'] = bin_counts[1] / bin_counts['total']
# 結果を表示
print(bin_counts[['white_ratio', 'black_ratio']])Out:
label white_ratio black_ratio
age_bin
0-20 0.694444 0.305556
21-30 0.647887 0.352113
31-40 0.742647 0.257353
41-50 0.697143 0.302857
51-60 0.700599 0.299401
61-70 0.670968 0.329032
71-80 0.693122 0.306878
81+ NaN NaNそのようにして計算した黒データ割合、白データ割合を用いて指標スコアを算出する。
# 5. 指標スコアを計算
bin_counts['score'] = np.log(bin_counts['black_ratio'] / bin_counts['white_ratio'])指標スコアを計算し、その値を基に各ビンを並べると、スコアがビンの特徴を反映しており、結果としてスコアに対する線形回帰が非常に良い当てはまりを示すことがある。これは、スコアが黒データと白データの比率の自然対数に基づいて計算されているためである。対数関数の性質上、データの相対的な増減がスコアに線形的に反映されるため、線形回帰が非常に適合しやすくなる。
4.2 特徴量の選択方法
実務では、50個以上のかなり多くの特徴量の候補があることがある。そのような場合、すべての特徴量を使用してしまうと「多重共線性」や「モデルが非常に複雑になってしまう(実際何が原因でアルゴリズムが動いているのかよくわからなくなってしまう)」等の問題が発生してしまう。
そこで、この章では数ある特徴量候補の中から特徴量を選択する方法について考えてみようと思う。
4.2.1 単変量解析
回帰分析においては、単変量解析を行う方法がある。単変量解析とは、特徴量の候補一つ一つを単独で説明変数とし、一つ一つの係数やR2スコアを確認する方法である。
係数やR2スコアの値が著しく低い場合は、特徴量としての重要性が低いことが示唆される。
注意点としては、Omitted Variable Bias (説明変数を省略することによって発生するバイアス)が内在している点である。Omitted Variable Bias とは、重要な説明変数をモデルから除外した結果、残りの変数に対する係数推定が偏ってしまうことである。具体的には、除外された変数が目的変数に対して影響を持つ場合、その影響が誤って他の説明変数に割り当てられるため、モデルの推定結果がバイアスを含むことになる。
単変量解析におけるリスク
単変量解析では、各特徴量を単独で分析するため、他の説明変数が与える影響を考慮に入れていない。このため、以下のようなリスクがある。
交絡効果の無視: ある特徴量が目的変数に影響を与えているように見えても、実際には他の説明変数との相互作用による影響である場合がある。単変量解析ではこれを無視するため、誤った解釈につながる可能性がある。
過大評価または過小評価: 重要な変数を省略することで、残った変数の影響を過大または過小に評価してしまうことがある。これにより、モデル全体の予測力が低下するリスクがある。
それでは、下記にiris datasetを使った例を示す。
In:
from sklearn.datasets import load_iris
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import pandas as pd
# データセットの読み込み
data = load_iris()
X = pd.DataFrame(data.data, columns=data.feature_names)
y = data.target
# 単変量解析結果を保存するリスト
univariate_results = []
# 各特徴量ごとに単独で線形回帰を行い、係数とR²スコアを算出
for feature in X.columns:
X_single = X[[feature]]
model = LinearRegression()
model.fit(X_single, y)
# 予測値を計算
y_pred = model.predict(X_single)
# 係数とR²スコアを取得
coefficient = model.coef_[0]
r2 = r2_score(y, y_pred)
univariate_results.append({
'feature': feature,
'coefficient': coefficient,
'r2_score': r2
})
# 結果をデータフレームに変換
univariate_df = pd.DataFrame(univariate_results)
print(univariate_df.sort_values(by='r2_score', ascending=False))Out:
feature coefficient r2_score
3 petal width (cm) 1.028071 0.914983
2 petal length (cm) 0.440424 0.900667
0 sepal length (cm) 0.774212 0.612402
1 sepal width (cm) -0.801924 0.182037この結果より、係数では2番のpetal length(花びらの長さ)が一番低く、R2スコアでは0番のsepal length(がくの長さ)が一番低いことが分かる。
4.2.2 手動で選択
また、決定木モデルにはfeature importance(特徴量重要度)を示す指標がある。feature importanceを確認しながら、重要度の低い特徴量を削除する方法についても見てみよう。
In:
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
import pandas as pd
# データセットの読み込み
data = load_iris()
X = pd.DataFrame(data.data, columns=data.feature_names)
y = data.target
# ランダムフォレストのトレーニング
model = RandomForestClassifier()
model.fit(X, y)
# 特徴量の重要度を取得
importances = model.feature_importances_
importance_df = pd.DataFrame({
'feature': X.columns,
'importance': importances
}).sort_values(by='importance', ascending=False)
print(importance_df)Out:
feature importance
3 petal width (cm) 0.482815
2 petal length (cm) 0.419608
0 sepal length (cm) 0.080040
1 sepal width (cm) 0.017538この結果より、irisデータについては0番目の特徴量であるsepal length(がくの長さ)が決定木モデルにおいて、特徴量重要度が低いことが分かる。
4.2.3 ステップワイズ法
ステップワイズ法とは、統計モデルや機械学習モデルにおいて、最適な説明変数(特徴量)の組み合わせを選択するための手法の一つ。この方法は、特徴量の追加または削除を繰り返しながら、モデルのパフォーマンスを最適化するプロセスである。
利点としては、自動的に説明変数が選択されるため、手動で選択する手間を省略できる。
欠点としては、過学習のリスクがあること、変数間の相関が強い場合、重要な変数が除外されるリスクがあることである。
特に、重要な説明変数が除外されるリスクがあるため、多くはステップワイズ法である程度の特徴量を選択した後、手動で重要な特徴量を追加する方法が一般的である。
ステップワイズ法はいまでもロジスティック回帰モデルなどでは広く採用されている説明変数の選択方法である。
詳細は下記ご参照。
下記に、iris datasetに対してRFECV関数(RFECVはsklearnライブラリの機能で、再帰的特徴量削減(Recursive Feature Elimination, RFE)と交差検証(Cross-Validation)を組み合わせて、最適な特徴量のセットを選択する手法)を使用した例を示す。
In:
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_selection import RFECV
from sklearn.metrics import accuracy_score
# データセットの読み込み
data = load_iris()
X = pd.DataFrame(data.data, columns=data.feature_names)
y = data.target
# データを学習用とテスト用に分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# ランダムフォレストを分類器として使用
classifier = RandomForestClassifier(random_state=42)
# RFECVの実行
rfecv = RFECV(estimator=classifier, step=1, cv=5, scoring='accuracy')
rfecv.fit(X_train, y_train)
# 選択された特徴量
print(f"Optimal number of features: {rfecv.n_features_}")
print("Selected features:", list(X.columns[rfecv.support_]))Out:
Optimal number of features: 2
Selected features: ['petal length (cm)', 'petal width (cm)']2つの選択された特徴量を使ってテストデータでの予測精度を確かめてみる
In:
# テストデータでの予測
y_pred = rfecv.predict(X_test)
# 正解率の計算
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy on test set: {accuracy:.2f}")Out:
Accuracy on test set: 1.00正解率が100%であった。
4.2.4 L1正則化やL2正則加項で特徴量を削減
最後に、L1正則化やL2正則化について説明する。
L1正則化やL2正則化についてChatGPTについて聞いたところ以下のような回答が返ってきた。わかりやすかったのでそのまま載せます。(妥協してすいません。。)
L1正則化とL2正則化は、機械学習モデルの過学習(overfitting)を防ぎ、モデルの一般化性能を向上させるための手法です。これらは、回帰モデルやニューラルネットワークの重み(係数)にペナルティを課すことで、モデルの複雑さを制御します。それぞれの手法について詳しく説明します。
L1正則化(Lasso回帰)
L1正則化は、重みの絶対値の合計にペナルティを加える方法です。数式では、以下のように表されます。
コスト関数

Loss: モデルの損失関数(例えば、平均二乗誤差)。
λ: 正則化パラメータ。これにより正則化の強さを調整します。
wi: 各特徴量に対する重み。
特徴
特徴選択に寄与: L1正則化は、いくつかの重みをゼロにする傾向があります。これは、モデルが不要な特徴量を排除することを意味し、結果としてスパース(疎)なモデルが得られます。
モデル解釈性の向上: ゼロになった重みは、対応する特徴量がモデルにとって無関係であることを示すため、特徴量選択のツールとしても使用できます。
使用例
Lasso回帰: L1正則化を用いた回帰手法で、特徴量選択の一環としてよく使われます。
L2正則化(Ridge回帰)
L2正則化は、重みの二乗和にペナルティを加える方法です。数式では、以下のように表されます。
コスト関数

Loss: モデルの損失関数。
λ: 正則化パラメータ。
wi: 各特徴量に対する重み。
特徴
重みの縮小: L2正則化は、すべての重みを小さくする傾向があります。重みが大きくなることを抑制し、モデルの過度な適合を防ぎますが、L1正則化のように重みをゼロにはしません。
特徴量のバランス: 全ての特徴量が一定の影響を持つため、特徴量選択には直接寄与しませんが、すべての特徴量を活かしたい場合に有効です。
使用例
Ridge回帰: L2正則化を用いた回帰手法で、すべての特徴量を考慮しながら過学習を防ぐために使われます。
L1正則化とL2正則化の組み合わせ(Elastic Net)
Elastic Netは、L1正則化とL2正則化の両方を組み合わせた手法です。
コスト関数

λ1: L1正則化の強さを制御するパラメータ。
λ2: L2正則化の強さを制御するパラメータ。
特徴
柔軟なモデル構築: L1正則化とL2正則化の利点を組み合わせることで、より柔軟な特徴量選択と重みの調整が可能になります。
使用例: LassoとRidgeの良いところを取り入れたい場合に使用されます。
正則化の選択
L1正則化は、特徴量選択が重要な場合(重要な特徴量が限られている場合)に有効です。
L2正則化は、全ての特徴量を活用したい場合や、特徴量が多いがそれぞれが有用であると考えられる場合に適しています。
Elastic Netは、L1とL2の両方の利点を活かしたい場合に選択されます。
まとめ
正則化は、モデルの過学習を防ぎ、より汎化性能の高いモデルを作るために非常に重要な手法です。どの正則化手法を選択するかは、データの特性や分析目的に応じて決定します。
以下に、例としてL1正則化による特徴量選択とモデルの評価を行ってみる。
In:
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# Irisデータセットの読み込み
data = load_iris()
X = pd.DataFrame(data.data, columns=data.feature_names)
y = data.target
# データを学習用とテスト用に分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# L1正則化を使ったロジスティック回帰のモデル作成
model = LogisticRegression(penalty='l1', solver='saga', multi_class='auto', max_iter=10000, random_state=42)
model.fit(X_train, y_train)
# モデルの評価
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy on test set: {accuracy:.2f}")
# 選択された特徴量の確認
non_zero_coefficients = np.where(model.coef_ != 0)[1]
selected_features = X.columns[non_zero_coefficients]
print("Selected features:", selected_features)Out:
Accuracy on test set: 1.00
Selected features: Index(['petal length (cm)', 'sepal length (cm)', 'petal length (cm)',
'petal width (cm)'],
dtype='object')第5章 モデルの評価方法について
第5章では、モデルの評価における指標のことや検証の方法が記述されていた。ここでは、特に重要だと思ったことを私なりにまとめてみようと思う。
5.1 交差検証
訓練データ、検証用データ、テストデータに分けて、精度の高いモデルができたとする。しかし、たまたま分割したデータの当てはまりがよく精度の高いモデルができた可能性ある。できるのであれば、データの分割方法に対して頑健なモデルを作成すべきである。
そんな時に有用な検証方法が交差検証(cross-validation)である。
交差検証は、データの分割方法を何通りも行いそのたびにモデルを作ることで、分割方法に対しての頑健性を考慮する検証方法である。
図にすると以下の通り。

それぞれ、白色が訓練データで黒色がテストデータである。
分割数は任意で決めることができ多くは5~10分割される。
交差検証は、sikit-learnのKFold関数、cross_val_score関数を使用すれば簡単に行える。
以下では、iris datasetを用いて、交差検証の例を見てみよう。
In:
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# Irisデータセットの読み込み
data = load_iris()
X = pd.DataFrame(data.data, columns=data.feature_names)
y = pd.DataFrame(data.target)
y.replace(2, 0, inplace=True)#2クラス分類なので、2を0とし、1:Versicolorの品種かどうかを識別する用のyを作成する
# データを学習用とテスト用に分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# L1正則化を使ったロジスティック回帰のモデル作成
model = LogisticRegression(random_state=0)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
#交差検証■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
from sklearn.model_selection import KFold, cross_val_score
#KFoldの設定(K=5)
kfold = KFold(n_splits=5, shuffle=True, random_state=0)
# 交差検証を実行
scores = cross_val_score(model, X_train, y_train, cv=kfold, scoring='accuracy')
# 各スコアの表示と平均スコア
print("各Foldのスコア:", scores)
print("平均スコア:", np.mean(scores))
# モデルの訓練(全体データで)
model.fit(X_train, y_train)
# テストデータでの予測
y_pred = model.predict(X_test)Out:
各Foldのスコア: [0.76190476 0.66666667 0.71428571 0.71428571 0.61904762]
平均スコア: 0.6952380952380952n_splits=5 は、データを5つの分割に分けることを指定しています。
shuffle=True は、データを分割する前にシャッフルすることを意味します。これにより、各分割がよりランダムなデータポイントを含むようになります。
random_state=0 は、シャッフルの際の乱数生成を制御するためのシードを設定しています。これにより、再現性のある結果が得られます。
交差検証での平均スコアが、問題に対する(今回の場合は、iris dataの2値分類問題)モデルの精度を示す。分割方法により精度に大きなばらつきがないか、最も精度の高いモデルはどれか などを考える必要がある。
(分割方法により精度のばらつきが少ない場合、基本的には最も精度の高いモデルが採択される。)
5.1.2 グループ付き交差検証
交差検証するにあたり、あるグループを分割の際に同じグループにしたい場合がある。例えば、画像識別で、ある人の顔を学習しほかの人の顔を当てるようなモデルの場合、ある人の特徴量はグループ1、ほかの人の特徴量をグループ2にする ようにしなければ、識別するにあたり、訓練モデルに答えが入ってしまうことになる。
そのような際に使用できるのがグループ付き交差検証と呼ばれるものである。
これはその名の通り、特定のグループが分割の際に同じグループ内に入るように制約を設ける方法である。下記に例を示す。
In:
from sklearn.datasets import make_blobs
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GroupKFold, cross_val_score
# データセットの生成
X, y = make_blobs(n_samples=12, random_state=0)
# グループの定義
groups = [0, 0, 0, 1, 1, 1, 1, 2, 2, 3, 3, 3]
# ロジスティック回帰モデルのインスタンス
logreg = LogisticRegression()
# GroupKFoldの設定 (n_splits=4)
cv = GroupKFold(n_splits=4)
# 交差検証を実行 (groupsをキーワード引数として指定)
scores = cross_val_score(logreg, X, y, cv=cv, groups=groups)
# 各Foldのスコアの表示
print("各Foldのスコア:", scores)Out:
各Foldのスコア: [0.75 0.66666667 0.66666667 1.]上記のように、cv = GroupKFold(n_splits=グループ(フォールド)数)を使うことで、各グループにはそれぞれのグループ(この場合はgroups0、1、2、3の4つ)に関する特徴量を持って分割を行うことができる。
5.2 グリッドサーチ
機械学習には、モデルを動かすうえで、自身で決定しないといけない変数(ハイパーパラメータ)がつきものである。ハイパーパラメータはこれといった決まりがなく、熟練技の一つであるが、どのハイパーパラメータを使えば精度が高くなるのかを知りたいときに便利な方法がある。それがグリッドサーチである。
グリッドサーチとは、ハイパーパラメータのすべての組み合わせを試して精度を算出する方法である。
以下にiris dataを使用した例を示す。
In:
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV, train_test_split
from sklearn.metrics import accuracy_score
# Irisデータセットのロード
iris = load_iris()
X = iris.data
y = iris.target
# データの分割: 訓練+検証 (80%) とテスト (20%)
X_train_val, X_test, y_train_val, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 訓練+検証データをさらに訓練 (70%) と検証 (30%) に分割
X_train, X_val, y_train, y_val = train_test_split(X_train_val, y_train_val, test_size=0.25, random_state=42)
# ロジスティック回帰モデルのインスタンス
logreg = LogisticRegression(max_iter=200)
# ハイパーパラメータの探索範囲の定義
param_grid = {
'C': [0.1, 1, 10, 100],
'penalty': ['l1', 'l2'],
'solver': ['liblinear', 'saga']
}
# グリッドサーチの設定
grid_search = GridSearchCV(logreg, param_grid, cv=5, scoring='accuracy')
# グリッドサーチを訓練データで実行
grid_search.fit(X_train, y_train)
# 最適なハイパーパラメータの表示
print("最適なハイパーパラメータ:", grid_search.best_params_)
# 検証データを使って最適モデルの性能を確認
y_val_pred = grid_search.predict(X_val)
val_accuracy = accuracy_score(y_val, y_val_pred)
print(f"検証データにおける精度:, {val_accuracy:.2f}")
# 訓練データ全体を使って最適なモデルで再度訓練
final_model = grid_search.best_estimator_
final_model.fit(X_train_val, y_train_val)
# テストデータでの予測と精度評価
y_test_pred = final_model.predict(X_test)
test_accuracy = accuracy_score(y_test, y_test_pred)
print("テストデータにおける精度:", test_accuracy)Out:
最適なハイパーパラメータ: {'C': 1, 'penalty': 'l1', 'solver': 'saga'}
検証データにおける精度: 0.93
テストデータにおける精度: 1.0コードの説明
データの分割
X_train_val, X_test, y_train_val, y_test
データセットを訓練+検証用(80%)とテスト用(20%)に分割。
X_train, X_val, y_train, y_val:訓練+検証用データをさらに訓練用(70%)と検証用(30%)に分割。
グリッドサーチ
訓練データ (X_train, y_train) を用いてグリッドサーチを実行し、最適なハイパーパラメータを見つけます。
GridSearchCV の cv=5 により、5分割交差検証を行います。
検証データでの評価
検証データ (X_val, y_val) を用いて、グリッドサーチで得られた最適なモデルの性能を確認します。
最適モデルでの再訓練
訓練+検証データ (X_train_val, y_train_val) を用いて、最適なモデルを再訓練します。
テストデータでの評価
テストデータ (X_test, y_test) を用いて、最終的なモデルの性能を評価します。
この方法で、訓練データ、検証データ、およびテストデータを用いたグリッドサーチを実行し、最適なモデルの評価ができます。
【メモ:パラメータの過剰適合について】
上記の例を見てわかったかもしれないが、上記では「訓練データ」「テストデータ」のほかに「検証用データ」の3つに分解してモデルを構築している。

ハイパーパラメータのチューニングを行う必要があるときは、モデルの構築に訓練データを使う。モデルを構築した後に、パラメータのチューニングを行うためのデータセットが必要なのである。
訓練データ、検証用データ、テストデータを区別することは、ハイパーパラメータの設定を行う過程を持つモデル構築には必須であるため留意しよう。
5.3 2クラス分類におけるモデルの精度指標
第2章や3章では、モデルの精度指標としてAcuracy(正解率)を使用していた。
正解率は
正しく分類されたサンプル数/総サンプル数
で計算される指標である。
しかし、モデルやデータセットによっては正解率以外の精度指標のほうが好ましい場合もある。精度指標を選択する際、常に機械学習モデルの最終的な目標を理解している必要がある。
この章では、ほかによく使用されるモデルの精度指標についてみてみよう。
5.3.1 混同行列
2クラス分類では、しばしば、偏ったデータセットを使う。”偏った”とは、陰性データが陽性データよりもずっと多い場合のデータセットのことである(その逆も然り)。
偏ったデータセットを使用し正解率でモデルの精度を図った場合、陰性データがあまりにも多すぎたとき、すべて陰性とモデルが予測しても、そのモデルの正解率は高くなってしまうのだ。
そんな時に使用するのが混同行列である。
混同行列とは、モデルの予測結果と実際の結果を2×2の行列で示したものである。
いかにiris dataでの例を示す。
In:
# Irisデータセットの読み込み
data = load_iris()
X = pd.DataFrame(data.data, columns=data.feature_names)
y = pd.DataFrame(data.target)
y.replace(2, 0, inplace=True)#2クラス分類なので、2を0とし、1:Versicolorの品種かどうかを識別する用のyを作成する
# データを学習用とテスト用に分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# L1正則化を使ったロジスティック回帰のモデル作成
model = LogisticRegression(random_state=0)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy on test set: {accuracy:.2f}")
# 混同行列の作成
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
conf_matrix = confusion_matrix(y_test, y_pred)
# 混同行列をDataFrameに変換し、ラベルを追加
conf_matrix_df = pd.DataFrame(conf_matrix,
index=['True: 0', 'True: 1'],
columns=['Pred: 0', 'Pred: 1'])
# 混同行列の表示
print("混同行列:\n", conf_matrix_df)Out:
混同行列:
Pred: 0 Pred: 1
True: 0 29 3
True: 1 9 4confusion_matrix関数を使えば簡単に混同行列を作成してくれる。Trueのほうが、実際のデータセットの0(陰性)と1(陽性)で、Predのほうが予測された0と1である。
上記の結果では、正解率は(29+4)/(29+9+3+4)=0.73… であるが、1を1として予測できた割合は4/(9+4)=30% であることが分かる。
混同行列は各成分に名前がある。

TN (True Negative)…実際の0を0と予測できた数
TP (True Positive)…実際の1を1と予測できた数
FN (False Negative)…実際の1を0と誤って予測した数
FP (False Positive)…実際の0を1と誤って予測した数
5.3.2 正解率(Accuracy)
混同行列の結果を一つにまとめた指標が正解率である。
正解率は今まで出てきていた精度のことで、混同行列における成分名で記述すると

となる。
(※精度とひとくくりにしている文献も数多くあるが、正解率、適合率、再現率のどれを指しているのか、計算式を確認して精査しよう。)
5.3.3 適合率(Precision)、再現率(Recall)、f1スコア
陽性と予測されたものが実際にはどれだけ陽性であったかを示す指標が適合率であり、計算式は

である。偽陽性(False Positive)を減らすことに焦点を当てている。
一方、実際の陽性サンプルのうち、陽性と予測された者の割合を示す指標が再現率であり、計算式は

である。偽陰性(False Negative)を減らすことに焦点を当てている。のちに紹介するように、真陽性率(True Positive Rate)というしようとして、ほかの精度指標の計算にも使用される。(名前が変わってしまうのはどうにかしてほしい)
適合率と再現率の調和平均でまとめた指標がf1スコアである。計算式は

である。これは適合率と再現率の双方を取り入れており、偏った2クラス分類データセットに対しては精度よりも良い指標である。
いかに、正解率、適合率、再現率、f1スコアについての例を記載する。
In:
from sklearn.metrics import classification_report, accuracy_score
# Irisデータセットの読み込み
data = load_iris()
X = pd.DataFrame(data.data, columns=data.feature_names)
y = pd.DataFrame(data.target)
y.replace(2, 0, inplace=True)#2クラス分類なので、2を0とし、1:Versicolorの品種かどうかを識別する用のyを作成する
# データを学習用とテスト用に分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# L1正則化を使ったロジスティック回帰のモデル作成
model = LogisticRegression(random_state=0)
model.fit(X_train, y_train)
y_pred = model.predict(X_test) #ここまでは上の例と同一=========================================================
# 精度、適合率、再現率、F1スコアの計算
accuracy = accuracy_score(y_test, y_pred)
report = classification_report(y_test, y_pred, target_names=['Class 0', 'Class 1'])
# 結果の表示
print(f"Accuracy: {accuracy:.2f}")
print("\nClassification Report:\n", report)
#f1スコアだけの計算
from sklearn.metrics import f1_score
# F1スコアの計算
f1 = f1_score(y_test, y_pred)
print(f"F1 Score: {f1:.2f}")Out:
Accuracy: 0.73
Classification Report:
precision recall f1-score support
Class 0 0.76 0.91 0.83 32
Class 1 0.57 0.31 0.40 13
accuracy 0.73 45
macro avg 0.67 0.61 0.61 45
weighted avg 0.71 0.73 0.70 45
F1 Score: 0.40上記の結果から、Accuracyでは0.7とまずまずの結果である者の、F1スコアでは0.4とあまり良い結果とはいえないことが分かる。
5.3.4 ROCカーブ、AUC、AR値(ジニ係数)
実務上では、上記で記載した通り閾値を設定する必要がある。モデルが様々な閾値でどれだけ正確にクラスを分類できるかを図示することができる。
ROCカーブは、真陽性率(TPR=TP/(TP+FN)、適合率と同義)と偽陽性率(FPR=FP/(FP+TN))を使ってプロットする。横軸にFPR、縦軸にTPRをプロットし、モデルの閾値を変えながら曲線を描く。
ROCカーブは、適切な閾値の設定に使用されることが多い。
また、ROCカーブの下の面積のことをAUC(Area Under the Curve)と呼び、精度してよく使用される。(f1スコアよりもこちらが使用されることが多い)
AUCは0~1の値を取り、1に近いほどモデルの精度がよいことを示す。
下記にiris dataにおけるROCカーブの描写と、AUCの計算の例を示す。
In:
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_curve, auc
# Irisデータセットの読み込み
data = load_iris()
X = pd.DataFrame(data.data, columns=data.feature_names)
y = pd.DataFrame(data.target)
y.replace(2, 0, inplace=True)#2クラス分類なので、2を0とし、1:Versicolorの品種かどうかを識別する用のyを作成する
# データを学習用とテスト用に分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# L1正則化を使ったロジスティック回帰のモデル作成
model = LogisticRegression(penalty='l1', solver='liblinear', random_state=0)
model.fit(X_train, y_train)
# テストデータに対する予測確率の取得
y_prob = model.predict_proba(X_test)[:, 1] # Positiveクラスの確率
# ROCカーブの計算
fpr, tpr, thresholds = roc_curve(y_test, y_prob)
# AUCの計算
roc_auc = auc(fpr, tpr)
# ROCカーブの表示
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='blue', lw=2, label=f'ROC curve (area = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='grey', linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic (ROC) Curve')
plt.legend(loc='lower right')
plt.show()
# AUCの表示
print(f'AUC: {roc_auc:.2f}')Out:

AUC: 0.80ROCカーブでは一番左上に位置する点が最もTPが多くFPが少ない点であるため、閾値の候補となる。
また、AUCは0.8となっており、高い精度を誇ることが分かる。AUCはモデルの目的にもよるのだが、だいたい0.7以上であればまずまずの結果であると考えることが多い。
当たり前のことなのだが、AUCはROCカーブ以下の面積を示している。つまり、モデルの閾値を変化してもAUCは変化しない(すべての閾値でのTPRとFPRの点が描く点を記しているので)。(実務でいろんなモデルや精度指標を使っているとついつい忘れがちなのだが、もし自身のモデルで閾値を変えてAUCが変化したときは、何かがおかしいので注意しよう。)
5.3.5 AIC
複数のモデルを比較したとき、同じような精度を示した場合、どのモデルを使用すればよいのだろう。モデルの複雑さで比較し、より単純な方を使用することがある。
AIC (Akaike Information Criterion)は、モデルの複雑さとデータへの適合度を確認するための指標である。計算式は

である。
パッケージではAICの計算は関数化されていないため、公式にしたがって計算する必要がある。以下に算出例を示す。
In:
import numpy as np
from sklearn.metrics import log_loss
# モデルの対数尤度の計算
log_likelihood = -log_loss(y_test, y_prob, normalize=False)
# モデルのパラメータ数の取得
n_params = len(model.coef_.flatten()) + 1 # 係数の数 + バイアス項
# AICの計算
aic = 2 * n_params - 2 * log_likelihood
print("AIC:", aic)Out:
AIC: 54.91110885847488複数のモデルを比較する際、最終的な使用の簡単さなどの定性的な理由でモデルを選択するケースもあるが、最もAICが低いモデルが選ばれるケースもある。
5.4 多クラス分類におけるモデルの精度指標
これまでは、2クラス分類モデルにおける精度指標について考えてきた。それでは、多クラス分類モデルではどうだろう。TPやFPなどの概念がないので、どのように考えればよいのか。
多クラス分類モデルでは、混同行列を描写し、各クラスの分類を目視で確認する場合がある。
また、多クラス版のf1スコアが最もよく使用される。
計算はまず、個々のクラスに対するf1スコアを計算し、3種類の異なる方法を用いてf1スコアを計算する。
1. macro
各クラスのスコアを均等に重み付けして平均を取る。
クラス間の不均衡が無視されるため、すべてのクラスが同じ重要度を持つ。
少数クラスと多数クラスの両方を同じ重みで扱いたい場合に使用する。
2. micro
全体の真陽性数、偽陽性数、偽陰性数を集計してからスコアを計算する。
サンプル数が多いクラスが全体のスコアに大きく影響する。
クラス間の不均衡があるデータセットで全体的なモデル性能を測るのに適している。
3. weighted
各クラスのスコアを、そのクラスのサンプル数に比例した重みで平均を取る。
クラスの不均衡を考慮に入れますが、サンプル数が多いクラスが支配的になる。
少数クラスが存在する場合に、全体の性能を公平に評価するのに有用。
以下に例を示す。
In:
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
# Irisデータセットのロード
iris = load_iris()
X = iris.data
y = iris.target
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
from sklearn.svm import SVC
from sklearn.metrics import confusion_matrix, accuracy_score, classification_report, f1_score
# SVMモデルの定義
model = SVC()
# モデルの訓練
model.fit(X_train, y_train)
# 予測
y_pred = model.predict(X_test)
# 混同行列の作成
conf_matrix = confusion_matrix(y_test, y_pred)
acc = accuracy_score(y_test, y_pred)
f1_macro = f1_score(y_test, y_pred, average='macro') # マクロ平均のF1スコア
# 混同行列をDataFrameに変換し、ラベルを追加
conf_matrix_df = pd.DataFrame(conf_matrix,
index=[f'True: {name}' for name in iris.target_names],
columns=[f'Pred: {name}' for name in iris.target_names])
print("Confusion Matrix:")
print(conf_matrix_df)
print(f"Accuracy: {acc:.2f}")
print(f"マクロ平均のF1スコア: {f1_macro}")Out:
Confusion Matrix:
Pred: setosa Pred: versicolor Pred: virginica
True: setosa 19 0 0
True: versicolor 0 13 0
True: virginica 0 0 13
Accuracy: 1.00
マクロ平均のF1スコア: 1.0マクロ平均で計算したf1スコアは1.0であった。混同行列をみても、すべてのデータポイントが正確に予測されていることが分かる。
