階層的クラスタリングについて知識を深めていこう！空間拡張性などにも触れていく

階層的クラスタリング

• デンドログラム(dendrogram)
  縦軸：クラスター間距離
  横軸：データ

階層的クラスタリングのメリット

• 上の図のように、誰がどのクラスターに属しているのか詳しく可視化することが可能！

Remark

階層的クラスタリングには２通りある

• 分割型⇨全体が一つのクラスタになった状態から始めて，再帰的に対象集合の分割を繰り返す。

• 凝集型⇨バラバラの状態にあり、この時点では全てはたがいに異なるクラスタに属しています。そこから、少しずつ大きなクラスタが形成されていく。

クラスター間の距離はどのように測るのか？

• 最短距離法

クラスターにデータが２つずつ存在する場合、２点間の距離を測る
その距離が最も近いデータ点の距離をクラスター間距離とする

• 最長距離法

クラスターにデータが２つずつ存在する場合、２点間の距離を測る
その距離が最も近いデータ点の距離をクラスター間距離とする

• 重心法

C1とC2のそれぞれの重心を求め、その重心間の距離を重心法という

• ウォード法

（a）C1間の重心間距離（ユークリッド距離）とC2間の重心間距離の合計と、
（b）C1とC2を合わせた時の重心間距離の合計
この(b)-(a)を最小にする！

クラスター間距離の性質

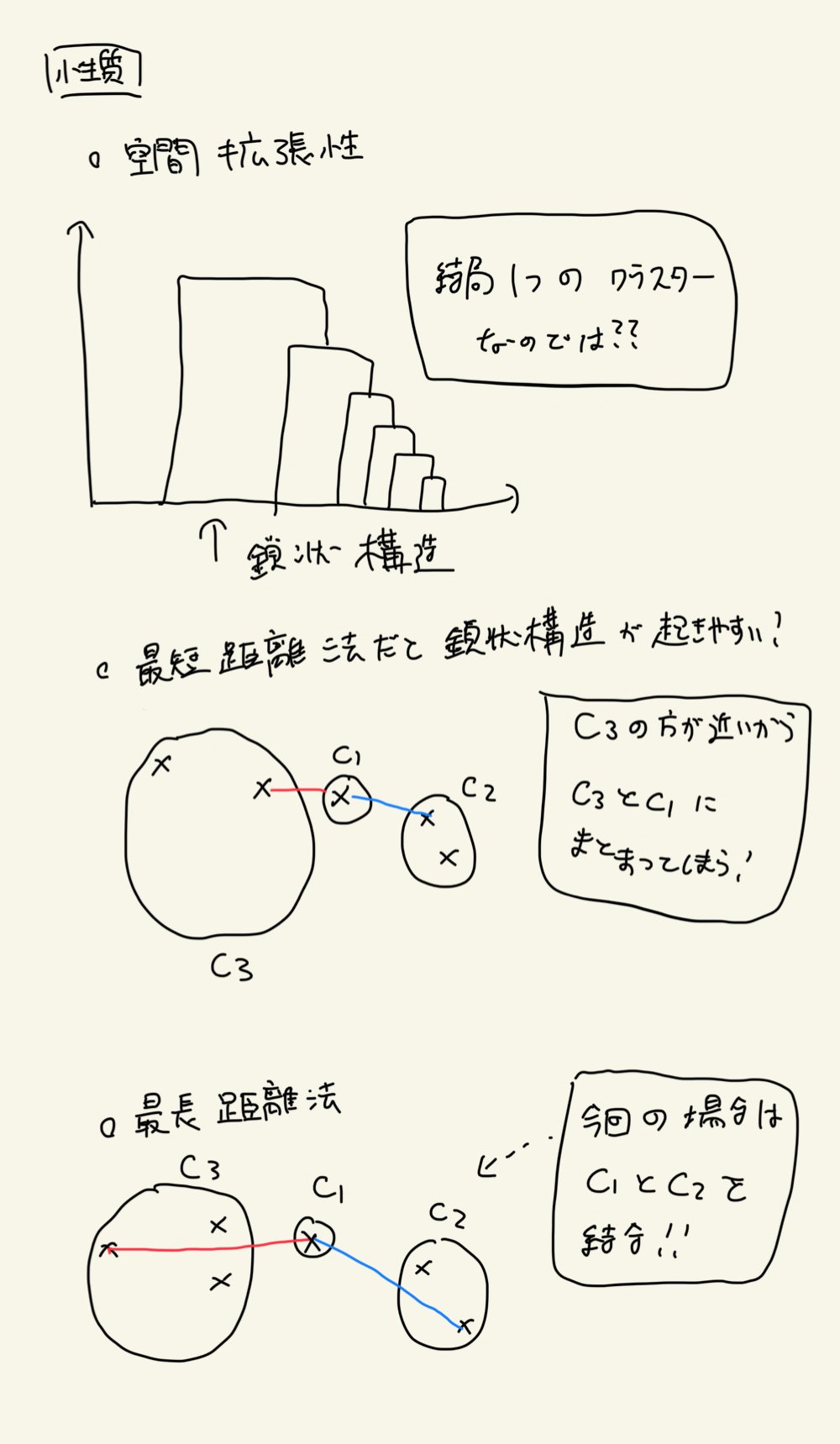
• 空間拡散性

序盤に出たクラスターがどんどん一人勝ちしてしまう様子
最短距離法が一つの例
最長距離法の場合は、逆に鎖状構造が起きづらい

• 単調性

これまでに結合した時のクラスター間距離＜
次に結合する時のクラスター間距離
三平方の定理を学んでおくと理解が深まる！

最短距離法にも大きなメリットが存在する

• Hartigan一致性

サンプルサイズが十分大きいとき
dendrogramが確率密度関数の一致推定量となる。