文字置き換えた方がスッキリするよね(電験二種理論H22問3)

もしかして花粉シーズンまだ終わってない…？

問3 過渡現象の問題

とにかく手順を間違えないことだねぇ。
分数多かったからその辺の間違いに注意しないとかな。
ではいつも通り丁寧に。

⑴、⑵について。
一瞬迷うやつ、スイッチが閉じてるという文章を発見すれば早い。
図を少し書き換えるとわかりやすいかな。

分圧の法則よりC1にかかる電圧はR2とR3にかかる電圧、C2にかかる電圧はR3にかかる電圧とわかる。
よって⑴の答えは(リ)、⑵の答えは(ニ)となる。

⑶、⑷について。
④という微分方程式が用意されてるのでこれを計算していけば良い。

まず求めたいqについている余計なものを外していく

次にdqとdtを両辺に分ける。

分数多すぎ笑
分数部分を少しわかりやすくして

両辺を積分する。

左辺の次は右辺。

二つの式を＝で結んでさらに計算。

eのD乗が知りたいのでt=0の時、q(0)がどうなるかを考える。
t=0の時、つまりスイッチが閉じた瞬間である。
閉じた瞬間の電荷は0である。
この考え方が最初よくわからなかったけど、電荷の式って電流×時間で時間=0なんだから電荷も0だわって納得している。
というわけでt=0、q=0を代入し計算すると

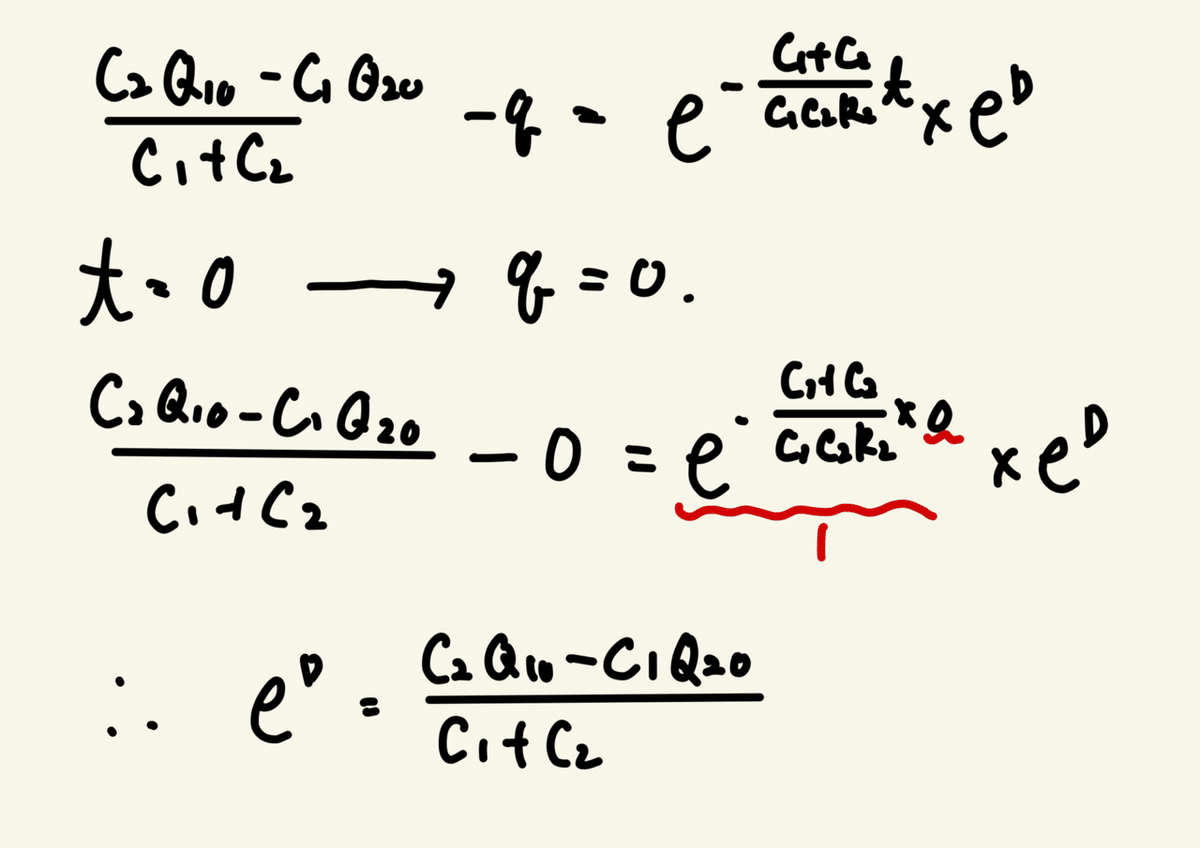
eのD乗を代入しqについて整理すると

以上より⑶の答えは(イ)、⑷の答えは(ホ)となる。

⑸について。
まずv1を計算してみる。

−∞乗ってのは便利だなあ笑
同様にv2も計算。

t＝∞とするとv1、v2は同じ値になることがわかった。
ということはそうなるグラフを選べば良い。
最終的に同値へと収束するのは

上記のグラフとわかる。
よって⑸の答えは(カ)となる。

あとがき

「レベルアップしたいこと」というnoteのお題があった。
山ほどあるなぁ笑
学力も体力も精神力も全部欲しい。
なんなら文章力も欲しいですわ笑

私はあの諺が嫌いなので二兎でも三兎でも追っていく。
欲張り上等よ笑

皆さんも欲しいもの手に入れましょー、ではでは。