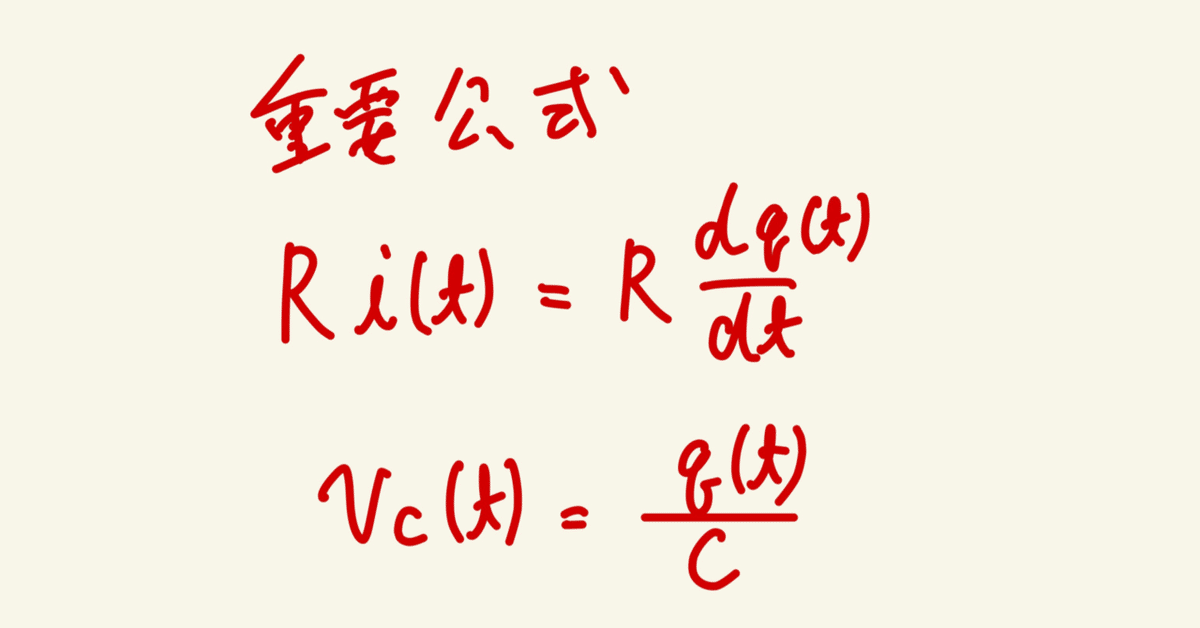
数学マジシャン(電験二種理論H21問4)

マジシャンのほんの一握りの中にガチの魔法使いがいると思ってたあの頃。

問4 過渡現象の問題

微分方程式を解く手順を忘れたが結果どうなるかは若干覚えている為、正解できたのもある問題。
申し訳ないがここはわからなくてもしばらくは選択肢を選ばせてもらう。

さて、どういう手順であったか…
やりながら思い出していく。

⑴、⑵について。
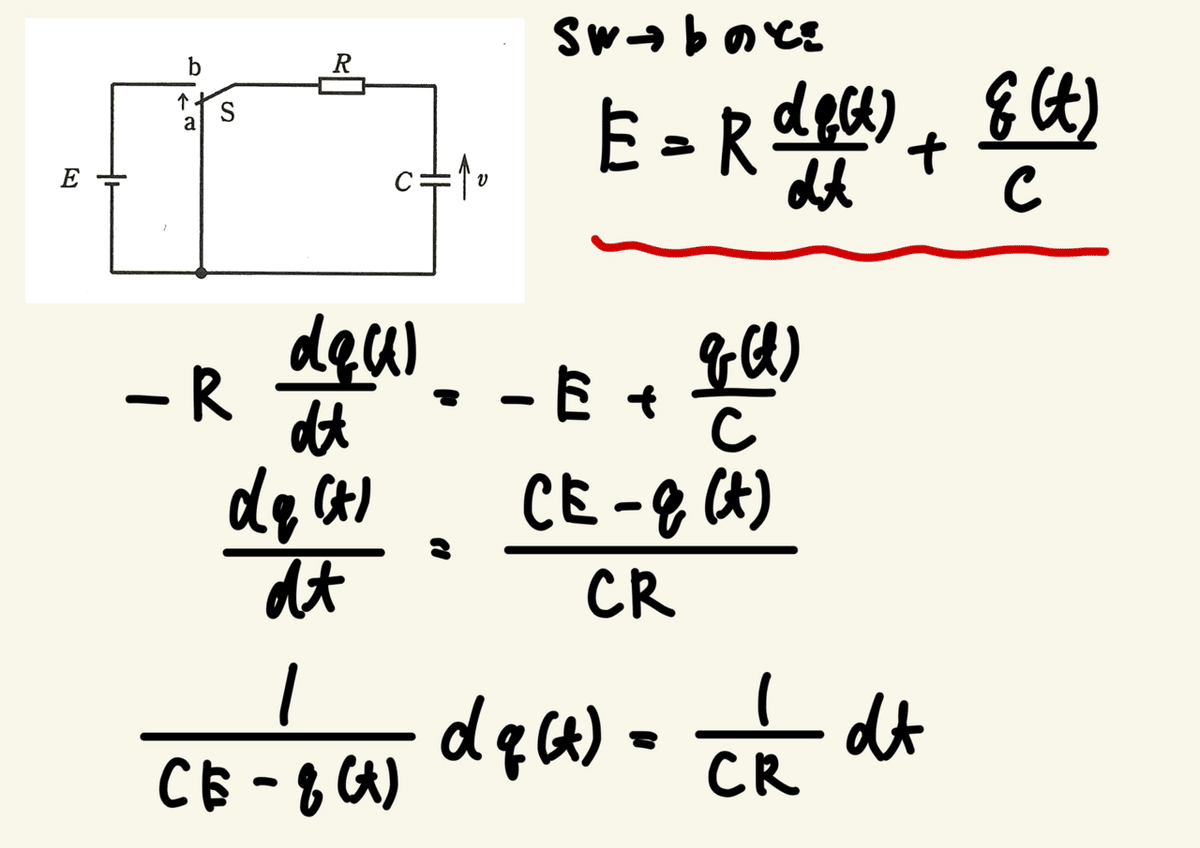
回路方程式をたてる。

まあこの式をいきなりかかれても意味不明である。

両方とも電圧のことであり、電荷Qで合わせたいので上の式にしている。
これを計算していくと

両辺積分すると

計算が複雑になるので右辺、左辺分けて考える。
まず左辺。

前はdナントカをなぜ置き換えることができるのかわからなかった。
文字置き換えて微分してるだけっていうね・・・
続いて右辺。

こっちはまあ簡単か。
両側計算したので統合し続ける。

AだのBだのDだのわかりづらいがここは仕方ない。
文字に決まりはないので好きなものに置き換えて興味を持つのもありかもね。

そんな訳でこのDを求めるのだがどうするか。
ここで使えるのが初期状態である。
つまりスイッチがa側の時、各値がどうなっているか考えれば良い。

これを先ほどの式へとぶっ込んでいくと

また先ほどの式に戻り

かなり問題文の式へと近づいてきた。両辺をCで割ると

ようやく⑴、⑵の答えに辿り着いた。
⑴は(リ)、⑵は(イ)となる。

初めてこの問題を解いた時、マジックでも見せられてるような気がしたのを思い出す。
あれよあれよと数値が変わっていく様をただただ書き写すしかできなかった。
今はまあ何やってるか分かるようにはなったから成長したなぁ…

⑶について。
数値を入れてみる、これに尽きる。

0から始まって限りなくEに近づいているグラフを選べば良い。
よって⑶の答えは(ヨ)である。
実は過渡現象時のコンデンサの電圧のグラフを知っているだけでこれは解けるんですけどね…

⑷について。
これも実際に2/3を入れてみればいい。

対数がわかっていればここは問題なく解ける。
よって⑷の答えは(ロ)となる。
割と綺麗な数値になるので解けると気持ちが良い。

⑸について。
⑷の式を使いT1の時とT2の時の式を考えて計算していくと

⑸の答えは(ヌ)となることがわかる。

あとがき

なんとかH21編が終わったー
ちなみに得点は

問7を選んだ場合は65/90点(約7割)
問8を選んだ場合は69/90点(約7割5分)

うむ、2年ぶりに解いた割には意外とできてるな。

この調子で詰まることなく進めば、二次試験の対策が早くできる。
というか早くやれるようにしないとね笑

そんな感じで続きます。
ではでは。