同値分割の「分割」とは何か？

同値分割というテスト技法があるのは、テストに関わる人たちであれば大抵知っていると思います。これは、英語でいうと、同値分割する行為をequivalence partitioningと言い、同値分割した結果をequivalence partitionと呼びます。同値分割した結果のことは同値クラス（equivalence class）とも呼びます。最近、これに関していろいろ熱い議論があって、その時に色々考えたことと、気づきがあったので書いておきます。

まず、日本語で「分割」と呼んでいるものが英語だとpartitionということに、何か疑問を感じませんか？私は正直言うと、最近まで深く考えなかったので、実際よくわかっていませんでした。最近、自分の中では完全解決したつもりだったのですが、なかなか話が合わないことが多いので、公開討論したくてこのnoteを書きます。

まず、Partitionってパーテーションですよね。会社の自分の席と人の席の間にある仕切り板みたいなやつがパーテーションですね。

パーテーションは、「区画」と訳すこともできます。テストで必要となる入力の全体領域（これをDomain,ドメインと呼びます）に仕切り板を入れて、区画で区切ることをequivalence partitioningと言い、区切った結果できた区画をequivalence partitionと呼びます。区画の中身のことはISTQBの用語集ではPortion（ポーション）と呼んでます。以下が最新（2019年3月現在）の用語定義です。

Equivalence partition：A portion of the value domain of a data element related to the test object for which all values are expected to be treated the same based on the specification.

同値クラスという言葉もありますが、「クラス」は「同じ性質のものをまとめたもの」と言う意味です。なので区画の中身でまとめたものはクラスです。クラスは、いくつか箱を用意して、そこに同じ性質のものを投げ込んで行くようなイメージを私は持っています。

この関係をイメージにすると、私は、この図のように考えています。

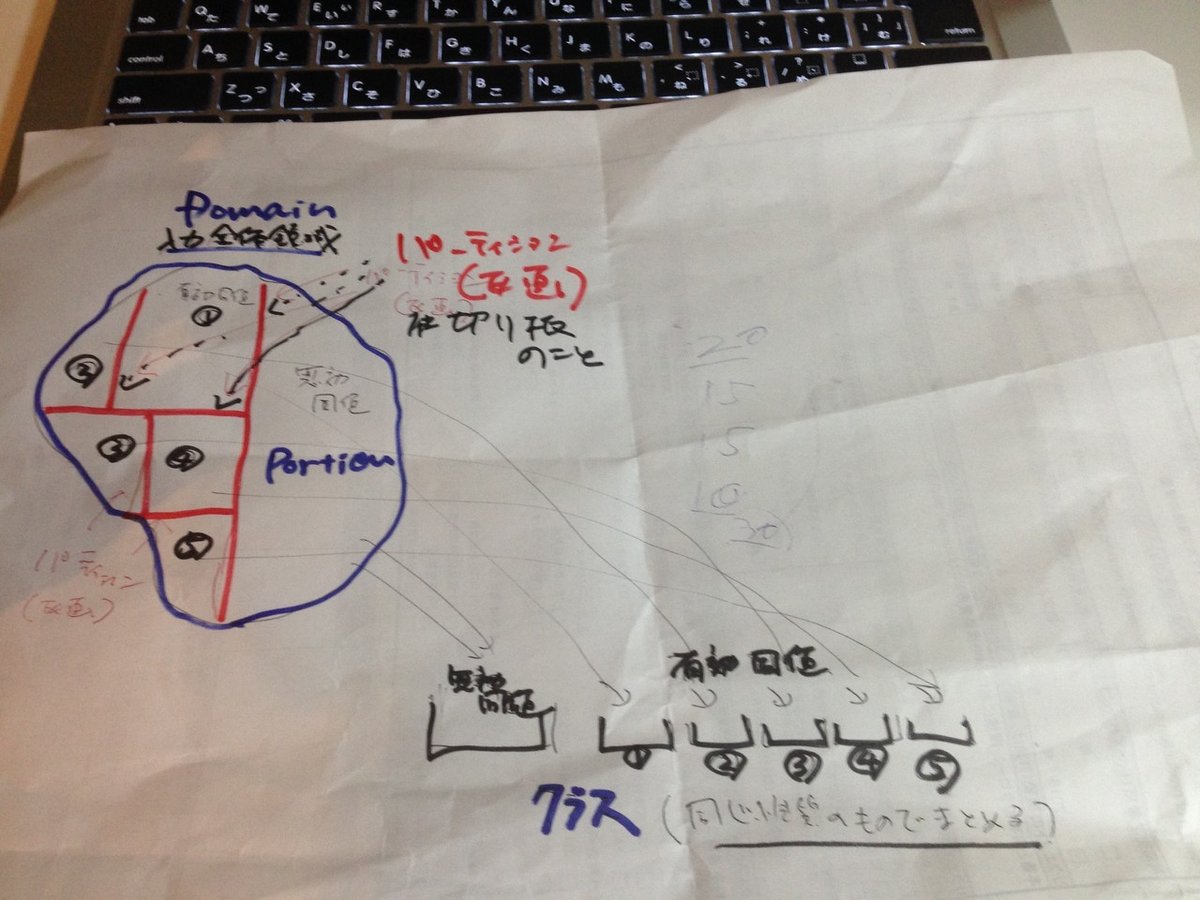
赤い線が仕切り線、つまりPartitionです。青で書いた入力の全体領域であるDomainに対してPartitionで仕切られた区画が、equivalence partitionで、このような仕切りを入れて区画を作ることをequivalence partitioning、つまり同値分割なんだとイメージできて、初めて同値分割の意味をちゃんと理解できたと思いました。同値クラスはequivalence partitionの中身、つまり「同じ性質の集まり」で分類した箱が別にあったそこに分類していったもののことだとイメージしています。なので、同じものを指すことには変わりないと思いますが、本質的に元々の領域に仕切り板を入れる「区画」とは違います。この本質的な違いが問題になるのは、同値クラスに対する境界値分析を行うときです。境界値分析は、同値クラスに属する値が連続しているレンジ（範囲）となっているときに使える考え方です。

ドメインのレンジに仕切り板を入れるイメージはこんな感じです。

レンジの適切なところに仕切り板をいれて区画を作るので、テストするときは、仕切り板とそのお隣さんを同値クラスの代表値として使いましょうというものです。私の理解では、Partition上にあるものをOn Pointと呼び、On Pointの外にあるものをOff Point、中にあるものをIn Pointと呼びます。

以下の絵のようなイメージです。

数字が連続してると仮に設定して、17が境界値だとしてみた例です。「＞＝17」の場合と「17＜」の場合で違う同値クラスになるってことです。17がOn pointです。「＜」の場合は、Onは無効値になり、「＞＝」の場合は、Onは有効値になります。（いわゆる、バイザーって言う著名なテストの人の本で書いてある、開いた、閉じたってやつです。）

これは、「同値クラス」のイメージでは境界がよくわからなくなってしまいます。境界値に仕切り板は１枚なはずですが、同値クラスの箱で考えると隣接する複数の仕切り板があるように考えられてしまいます。けど、そんなことテストケースの洗い出しで考えられないです。仕様からちゃんと境界値、つまりOnPointを分析しなければならないのはそう言う理由だと思います。
これは私の理解ですので、何かご意見があれば受け付けます。みんなの意見をまとめて海外の第一人者、例えばポールジョーゲンセンに質問してみるのも良いと思います。