境界値分析で分析する境界「値」について

テストケースを設計するためのテスト技法に境界値分析という技法があります。表紙の写真は新幹線の３列席ですが、真ん中の席のテーブルのギリギリにペットボトルがあります。これが境界値のイメージです。

境界値分析の定義の引用

以下にJSTQBのFLシラバス2018年度版に書かれている、境界値分析の説明を引用します。

境界値分析（BVA）は同値分割法の拡張であるが、パーティションが数値または順序付け可能な値で構成される場合だけ使用できる。パーティションの最小値および最大値（または最初の値と最後の値）が、境界値である（『Beizer 1990』）。

BVAってなんだ？って思う人のために一応書いておくとBoundary（境界）のValue（値）をAnalysis（分析）することの略です。

ある範囲の区切りに対して、境界値は１つ

境界値分析をした場合、その名の通り、同値分割法で区切ったパーティション上の「値」をテストすることになります。なぜか境界値分析なのに境界は値と値の間にあるようなことを示す場合がありますが、境界「値」分析という言葉の通り、境界値はある範囲の区切りに対して１つであり、その値がどこになるかを分析するのが境界値分析です。（同値パーティションの区切りには通常、最小の値と最大の値があるので、両方合わせると2つになります。）

少し前に同値分割法についてnoteに書きましたが、その時に境界値が1つであることを説明したイメージ図を再掲します。

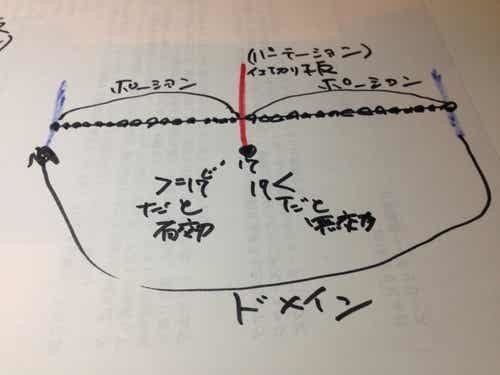
赤い板がパーティションで、パーティションの先の●が境界値です。この境界上の値をONポイントと呼ぶこともあります。パーティション上にある値なのでONなのです。複数の値をONすることはできません。

誤解のある表現

もう少し、シラバスを引用してみます。

例えば、ある入力フィールドで1桁の整数値が入力できる場合を考える。キーパッドで入力を制限し、整数値以外を入力不可にする。有効な値の範囲は、1～5である（1と5を含む）。この場合、（小さい）無効、有効、（大きい）無効の3つの同値パーティションが存在する。有効同値パーティションの境界値は1と5である。（大きい）無効同値パーティションの境界値は6と9である。（小さい）無効同値パーティションの境界値は0だけである。

このシラバスの記述は、実はとても問題があって、誤解を与えかねない記述になっています。（なのでこのnoteを書いています。）境界値分析では、ONポイントと隣接するポイントを選択してテストケースにして、ONポイントを間違えてコーディングしまっていないかを見つけるのが狙いなのですが、この記述では、選択したものを全て境界値と呼んでいるので誤解をあたえかねないなと思っています。

シラバスに書かれた例は、コーデイングしたイメージは以下のようになると思います。シラバスの文脈から、1桁の正の整数以外は物理的に入力できないってことなので、きっとコーディング上の制御はないはずです。

if(n >= 1 && n <= 5){
    　　printf("valid range.¥n");
  }else{
   　　 printf("invalid range.¥n");
}

このような範囲を指定している場合、＞＝と＞を間違えるといったことがよくあるというところから「境界値をちゃんと分析してテストしようね！」ということになったと考えられます。境界値分析は境界値に対して２ポイント選ぶ場合と、３ポイント選ぶ場合があるのでそれぞれについて解説していきます。

境界値の範囲に含まれる値と含まれない値をテストケースとする（2ポイント境界値分析）

2ポイント境界値分析を適用すると、テストしなければならない値は、境界値に対して分析をした区切り1つに対して2つです。1以上〜5以下を有効な範囲とした場合、以下の図のように1（最小値）と5（最大値）に対して区切り板が入るので、有効な範囲の中の最小値と最大値と[最小値−1]と[最大値＋1]の4つとなります。したがってテストする値は、0、1、5、6となります。

一方、有効な範囲よりも大きな値となる無効な範囲に着目した場合、5超〜9以下が無効な範囲です。無効な範囲としてテストする値は、5、6と9になります。（10は物理的に入力制御されている前提。）

分析した結果判明した無効な範囲の最小値(5超)と有効な範囲の最大値（５以下）は同じになることに注目してください。これは、正常なデータの最大値を不等号で表すと<=5となるのに対して、無効なデータの最大値を不等号で表すと>5となるためです。

不等号にイコールが入る場合は、境界値とその１つ外の値を選びます。

イコールが入らない場合は、境界値とその1つ中の値を選びます。

このように、連続する同値パーティションの隣接する境界値は重複します。境界値は1つというのはそういう意味です。なので、境界上にある値、つまり、●があるONポイントは「5」だけです。

境界値とその両隣をテストケースとする（3ポイント境界値分析）

３ポイント境界値分析の場合、テストしなければならない値は、境界値に対して分析をした区切りに対して3つです。有効な範囲のテストする値は、0、1、2、4、5、6の6種類になります。3ポイントで分析する場合、境界値に対して1つ少ない値と1つ多い値をテストする値として選択するためです。

3ポイント境界値分析法は、2ポイント境界値分析法でのイコールがある場合とない場合の選択する値の違いによるミスを防ぐための考え方です。そのため、有効な範囲より大きい無効な範囲に着目した境界値も、4、5、6になります。このように3ポイント境界値分析法を選択した場合でも、2ポイント境界値分析法と同様に、連続する同値パーティションの隣接する境界値は重複します。

テストケース数は隣接する境界値の重複だけ少なくなる

境界値分析は、「パーティションが数値または順序付け可能な値で構成される場合だけ使用できる」ものなので、実際は必ず隣接するいくつかの同値クラスが出てきます。テストケースの数は、隣接する区切りが重複した分だけ少なくなります。これまで解説してきた例で、具体的にいくつになるかを書いてみます。

２ポイント境界値分析の場合
有効同値クラス　0,1   5,6
無効同値クラス　0,1   5,6  9

重複する分を取り除くと5つになります。

3ポイント境界値分析の場合
有効同値クラス　0,1,2   4,5,6
無効同値クラス　0,1,2   4,5,6  8,9

重複する分を取り除くと8つになります。

値と値の間には何もない

境界値分析は、「パーティションが数値または順序付け可能な値で構成される場合だけ使用できる」ので、分析する際に順序づけできる値の単位も分析して明らかにします。そして、その単位で隣接する値を定義します。

例えば、今までの例で示している整数の「5」と「6」の間にある値、例えば5.1とか、5.01などはテスト対象ではないということです。なので、5と6の間には区切り板を入れることはできません。

まとめ

・境界値分析は同値パーティションが数値または順序付け可能な値で構成される場合だけ使用できる
・パーティションで区切った仕切り板の上にある値をONポイントと呼び、これが境界値である
・パーティション上の境界値は１つ
・連続する値と値の間にある値は考慮しないのでそこに仕切り板入れられない
・隣接する同値パーティションの境界値は重複するので、テストケースにした際にはその分数が減る