【算数オリンピック2013ファイナル第？問】補助線を引く三角形の面積問題

ラ・サール中学校の入試問題を取り上げている最中ですが、面白い問題がありましたので取り上げたいと思います。きっかけは YouTube に以下の動画がリストされたからです。

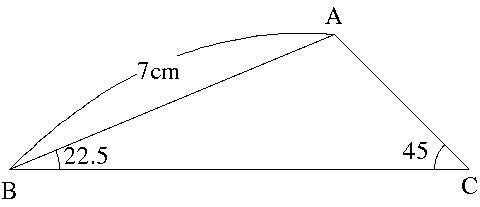
問題

三角形ABCは角ABC＝22.5度，角ACB＝45度，AB＝7cmです。三角形ABCの面積を求めなさい。

解答解説

長さが AB = 7cm しか与えられてない以上、感覚的には 7 × 3.5 ÷ 2 = 12.25cm2 となりそうですが、ちゃんと説明できますか？という問題です。

これに対して次のように補助線を引いてみました。

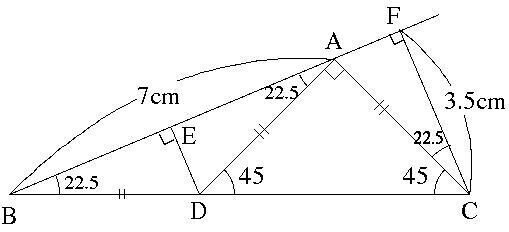
点の順番と考えた順番がバラバラなのですが、まず最初に点 C から 直線 AB に垂線を引いて、足(交点)を F とします。これを引いた目的は、辺 AB を底辺たときに CF が高さになるからです。

このとき、角 ACF = 180 - 90 - 25.5 - 45 = 22.5度 になることを確認します。角 ABC と同じ大きさなので、何か関係ありそうという話になります。

先ほど直感で 3.5cm と予想していたので、何となく二等辺三角形を描きたくなります。

そこで、辺 AB と 22.5度になるように点 A から直線を引き、BC との交点を D とおきます。これで三角形 DAB は AD = BD の二等辺三角形です。このとき、角 CAD を確認します。

まず、角 CAB = 180 - 45 - 22.5 = 112.5度 となります。したがって、角 CAD = 112.5 - 22.5 = 90度 となります。ということは、三角形 ACD は AC = AD の直角二等辺三角形になります。

これで材料はすべてそろいました。

点 D から直線 AB に垂線をおろし、その足(交点)を E とおくと、三角形 ADE と三角形 BDE が同型になるのはすぐに分かると思いますが、実は三角形 CAF とも合同になります。3つの角すべてで等しいのはいいと思いますが、あとは二等辺三角形を使って AD = BD = CA が成立するので、一辺とその両端の角が等しいことになります。

ということは、AE = BE = CF = 7 ÷ 2 = 3.5cm となるので、三角形 ABC の面積は AB × CF ÷ 2 = 7 × 3.5 ÷ 2 = 12.25cm2 でおしまいです。

感想

この問題は「問題の条件をどう見るか」を考えるのにいい問題だと思います。

22.5度という角度をどのように考えるか、辺の長さがほとんど与えられていない中で面積を出すためにどんな知識を使えばいいか、いろいろなことが試されます。

22.5度を見て 45度の半分と考えるのは当然で、その考え方から三角形 ABC をひっくり返して辺 BC で合わせて四角形を作ることを考える人もいるかと思います。

YouTube の解法はその考え方に基づいています。

私の場合は「CF の長さを求められないわけがないでしょ、面積が求められるんだから」という方針で最初に垂線を引きました。

解法はその人の考え方で変わってきます。多少の時間的な差は出るかもしれませんが、時間が許す限りはどれを取ってもいい訳です。

一つの問題からあなたは何を感じるか。

難しい問題を見たとき、最初は何も感じることができないかもしれません。それでも何かを感じようと意識して眺めるていくと、そのうち少しずつ感じられるようになると思います。それは正解に一歩近づいたことを意味します。

そうやって考え抜いた人ほど算数や数学が得意になると私は思いますし、少なくとも私はそうやって得意になりました。

考えても分からない・解けないのは苦痛かもしれませんが、その時間は無駄ではありません。少しでも問題から何かを感じられるよう、考える習慣をつけて頂けたらと思います。