見出し画像

Tableau｜曲線を描こう

yuko.n

yukoです。実はこれがずっとやりたかった。
本当のやりたいところには届いていないけど、最初の一歩。


１．偶然ってすごい

高校生と三角関数の勉強して（さぼって）たときに、きむ兄さんのTweetを発見。曲線だ～～～～！


２．曲線いろいろ

Tableauはプロットした点をパスでつないて線にすることができる。
点をプロットするには、X座標・Y座標がわかればいい。
曲線の方程式は「媒介変数表示」にすると、X座標・Y座標の計算式になる。

ということで「有名曲線のグラフ・式一覧」に全面的にお世話になります。

３．データの準備

プロットするためのデータ（-1から1の範囲で0.0001刻み）を用意します。
刻みが多いと点が増えるのでなめらかな曲線になります。

こんな感じ。項目名「#」とします。


４．円を描いてみる

ちょっと懐かしい公式を確認。

a=1としてすすめます。

計算式（x1、y1）を作ります。
「#」をかけることで、角度が変化します。

計算式（と関数）はこんな感じ。

①「x1」を列、「y1」を行に入れます。（点がプロットされた状態）
②「#」を詳細に入れ、マークを「線」にします

円が描けた！


５．正葉曲線（バラ曲線）を描いてみる

こちらも公式を確認。

今度は「a」をパラメーターでセットします。

バラ曲線は定数「a」が変わると形が変わるので、パラメータ使います。
詳しくは、こちら。

計算式（x5_p、y5_p）、パラメーター（n）を作ります。

[x1]と[y1]は先程の式、パラメータ範囲は、増減OK


作り方は同じ
①「x5_p」を列、「y5_p」を行に入れます。（点がプロットされた状態）
②「#」を詳細に入れ、マークを「線」にします
③パラメータ「n」を表示します。

これは n=8

動かしてみました。

n = 1 ~ 4

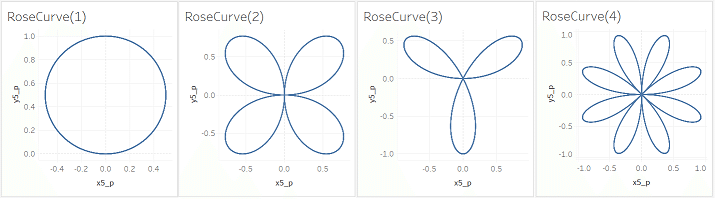
動くのはこちらからどうぞ。
https://public.tableau.com/app/profile/yuko.nakamura/viz/Curves_16694727261990/curves


参考サイト

有名曲線のグラフ・式一覧（カージオイド・サイクロイドなど） | 受験辞典 (univ-juken.com)

追記（2024/12/22）

この記事を書いた当時、よくわからなかったとこがめちゃめちゃわかりやすく説明されてる！というおつうさんの記事はこちら。


いいなと思ったら応援しよう！