
【みこAI】人間もPCもフリーズするからすばらしい!とチューリングもゲーデルも言った(はず)
では【みこAI】行ってみよう〜٩(ˊᗜˋ*)و
楽しそうだじょ(^~^)
最初に、この【みこAI】シリーズ記念すべき第1発目サムネイルのおじさんの悲劇から話を始めます。
多分、残業して終電に間に合わすぞ!って頑張っていたら、パソコンがフリーズしたんじゃないですかね(笑)。そんで、同時におじさんもフリーズした。あるいは、量子のもつれでおじさんのフリーズがパソコンに乗り移ったんでしょうか(笑)。
どっちにしても(笑)、いや笑えない状態です。
文系の人だけでなく、理系の人、いや、理系の人ですでにゲーデルについて十分に知っている人も手にとって絶対損がないのがこの本です。
この本の冒頭はこんな出だしです。
あ、パソコンがフリーズしちゃった! 全身から血の気が引いてゆく。背筋に悪寒が走る。なにしろ、徹夜の作業がすべて消えてしまう可能性があるのだ。
実際、一昔前のパソコンだったら、フリーズして、それでおしまいだった。泣こうが喚こうが、消失したデータは返ってこない。仕事を数分おきにセーブしていなかった自分の責任だ。
ちょっとフリーズの極限状況を考えてみよう。
たとえばあなたが株をやっていて、運悪く「大暴落」の瞬間に遭遇してしまったとしよう。あなたの財産はほとんどが株式になっている。今すぐに手を打たないと大変なことになる……と、被害を食い止めるために株を売ろうとした瞬間、あなたのパソコンがフリーズした! もはや、御愁傷様としかいいようがない、最悪のシチュエーションだ。呪ってやる~。
まあ、パソコンをつくっている会社も、これほどではないにしろ、フリーズの怨念の深さに気づいたのか、データを自動セーブする仕組みを開発したりして、人々が運命の波に翻弄されるのを避けようとしてきた。
おいおい待てよ、竹内薫は、いったい何が言いたいのか。
いや、もちろん、フリーズの背後にある問題について考えてみたいのだ。それが本書のテーマと深く関係しているから。
アラン・チューリングとクルト・ゲーデルの二人の大天才の研究の結論から言いますと、この世の中からフリーズは永久になくなりません(笑)。あはは、今度こそ笑わないとだめかもしれません。
と……このように宣言すると、いや!そんなことはないぞ。ムーアの法則に従って、コンピュータは果てしなく処理能力が向上するから、いずれはフリーズなんかしなくなるだろう。
という声が聞こえてきそうです。
では、竹内薫さんが例に出している株式の大暴落はどうでしょうか。経済学が発展していったらいずれ、大暴落というのはなくなるのでしょうか。

いつか完璧な予測計算で
大暴落も無くせそうな気がするが……
こっちはなさそうな感じがしますよね、どこまで経済学的分析が進んでも株式の大暴落はなくならないと思えます。そんな理論があるのなら、株式をやれば全員儲かることになってしまいますもんね。
この二つは、実はチューリングとゲーデルが取り組んだことと関係している、いえ、取り組んだ核心そのものだったのでした。
まずはチューリング的にパソコンのフリーズ問題を考えてみる
再び竹内薫さんの文章を引用します
実は、フリーズにもいろいろな原因があるのだが、その一つに「無限ループ」の存在があげられる。
プログラムの多くは「くりかえし」の方法で計算がおこなわれる。学校の数学の時間に「帰納法による証明」というのを必ず教わるが、アレである。実生活には全く必要ないから、学校を卒業すると、ほとんどの人は忘れてしまうが、目の前のパソコンの中で、帰納法は地道に使われていたんですねぇ。
で、無限ループというのは、その計算が文字通り、無限にくりかえされてしまう現象を指す(ループは「環」という意味)。くりかえしの計算では、計算が1行目から始まって、いったん最終行の一つ手前までいくと、ふたたび1行目に戻る。もちろん、帰納法はくりかえし作業であり、1行目に戻ること自体は問題ない。だが、やがて、どこかで計算を終えて、最終行の命令――すなわちEND――に到達しないとまずい。
万が一、「永遠にくりかえし続ける」ことになったら、パソコンは、あなたに応答することすらできない。無限ループの計算に手一杯で、あなたがキーボードやマウスから命令を伝えても、その命令を処理することができなくなってしまう。
このだが、やがて、どこかで計算を終えて、最終行の命令――すなわちEND――に到達しないとまずい。というところが問題ですよね。
ここを説明するのにさっき出てきた数学的帰納法を説明すれば、無限ループがなくならないことが証明できるのですが、数学的帰納法を使うと、このシリーズが読まれなくなるのは必至( U_U)。
そこで、Pythonで簡単な説明をしてみます。
たった一行の違いでフリーズは作れます(゚0゚)
そうそう、前回の記事でPythonの公式サイトからダウンロードできるって書きましたけど、もっといいの見つけたよ!
ブラウザから打ち込んでそのまま走らせるサービスありました。スマホからでも普通に動きました。
さっそく、ループ処理を書いてみました。

5回正常に繰り返しています。
これはつまりフリーズしていない状態です。
頑張って残業しています。
イヒヒ( ̄▽ ̄)これをフリーズさせます。

エラーが出てますよね。File too largeというのは、無限ループに陥っていて、結果が無限になっているので出力できませんということです。
さっきはこうなってました。
0回目のみこちゃん文
1回目のみこちゃん文
2回目のみこちゃん文
3回目のみこちゃん文
4回目のみこちゃん文
ところが、上の赤矢印のところはこうなってまして……。
#num += 1 この行をコメントアウト
つまり、最初の正しいプログラムは、5まで繰り返すけど、毎回1足しましょうね#num += 1というのがあったのです。でもこれをコメント扱いにして(#をつけるとこれはプログラム部分じゃないよということになるのです)しまうと、永遠に足されないので5まで行かないのでした。
5(゚0゚)5時だよ5時!退社時間!(公務員だけか……)。
最初のプログラムは5時になったら退社していいよ!っていう行が入っていたんだけど、5時になったら無限ループから抜けていいよ、というたった1行のコードを抜かすと、とたんにブラック企業になる(爆)。従業員は毎日深夜終電後にフリーズして程なく入院するでしょう。
人為的ミスではなく必然的に無限ループは起きてしまう
今は、人為的ミスで無限ループのフリーズを起こしてみました。じゃあ、プログラマがミスをしなければ、フリーズは世の中からなくなるんじゃないの?と思うと思います。みこちゃんも、プログラミングを趣味でやっているときは素朴にそう考えていました。
でも、チューリングとかゲーデルの本読んだら、それが妄想だと分かりました。
どんなに完璧にプログラミングをしても、世界からフリーズはなくならないということを、ふたりとも仲良く言っていたのです。
ゲーデルについてはまた別に書きます。チューリングについて簡単に書いてこの記事を終えます。
チューリングマシンっていう万能機械があります。これを何でもできてしまうコンピュータの始まり!って解説しているネット記事があるのですが、途方もないデタラメです。
チューリングマシンでチューリングが言いたかったのは、コンピュータの限界です。でも否定的な話じゃありません。ここまでは完ぺきにできるけど、こっから先はできない、という感じでコンピュータの凄さを説明したわけです。カントが『純粋理性批判』で理性の働きを説明するときにやった方法とまったく同じですね。
ここに、非常に良い記述があります。
アラン・チューリングは1936年、停止性問題を解くアルゴリズムは存在しないことをある種の対角線論法のようにして証明した。 すなわち、そのようなアルゴリズムを実行できるチューリングマシンの存在を仮定すると「自身が停止するならば無限ループに陥って停止せず、停止しないならば停止する」ような別の構成が可能ということになり、矛盾となる。
「自身が停止するならば無限ループに陥って停止せず、停止しないならば停止する」
平たく言い換えればこういうことです。
num = 0
str = "回目のみこちゃん文"
while < 停止するまで:
print(num,str)
num += 1
これは、プログラミング構文的には完璧で、どこにもミスはありません。
でも、条件が鬼(爆)。
while < 停止するまで:
( U_U)
このプログラムが停止するかどうか、停止するまで調べなさい。
キヒヒヒヒ( ̄▽ ̄)。
走らせてみましょう。
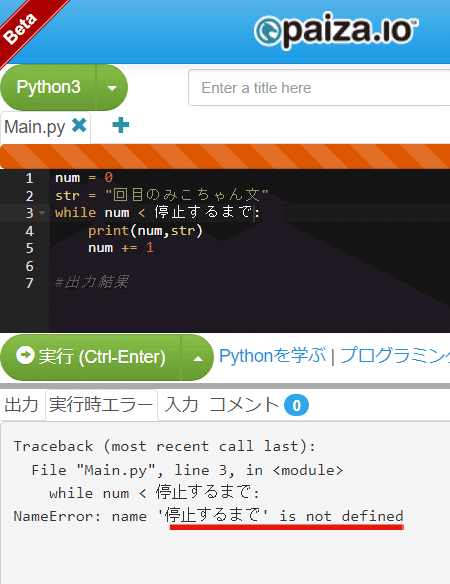
停止するまでが定義されていない(is not defined)のでエラーが出ましたね。
残業銀行員の悲劇はなんとかなるが万能チューリングマシンの不完全性は解消されない
ある銀行の午後8時。手計算でやっている入金伝票と出金伝票が合わないとします。そうすると、銀行は(その支店は、その支店長の出世は)存亡の危機にさらされます。

(゚0゚)もう全員ミスが見つかるまで死ぬまで計算します。文字通りこれです。
while num < 入金伝票と出金伝票が合うまで
銀行業務は完全に簿記システムなので、どっかに人為的ミスがあることは明白なので、これはやがては見つかるはず(もし、人為的に悪意でだれかがやていなければ)。
でも、さっきのwhile num < 停止するまではちょっと性質が違いますよね。
停止するかどうか停止するまで判定するわけです。
もしプログラムにバグがなければ、どこにも欠陥がないので、このプログラムは永久にループし続けます。あれ(゚0゚)ってことは、無限ループに陥っているから、それって無限ループバグがあるってことになる!
逆もそうですよね。もし、無限ループバグがあるのであれば、停止するまでっていう条件をつけてもらっても、無限ループに必然的に陥ります。
つまり、万能チューリングマシンは無限ループに陥るかどうか決定不可能マシンだ、と言い換えることができます。
つまり、万能チューリングマシンは夢の万能機械だ!って少しでも言っているネット記事が大嘘だ(どころかチューリングが言ったことと正反対だ)というのがわかります。
ほら!ここで!万能チューリングマシンはゲーデルとつながったのだ

カンの良い方は、この部分、どっかで見たことあると思うでしょう。
もしプログラムにバグがなければ、どこにも欠陥がないので、このプログラムは永久にループし続けます。あれ(゚0゚)ってことは、無限ループに陥っているから、それって無限ループバグがあるってことになる!
逆もそうですよね。もし、無限ループバグがあるのであれば、停止するまでっていう条件をつけてもらっても、無限ループに必然的に陥ります。
これでした!
古代ギリシャ七賢人の一人、エピメニデスにまつわる論理的逆説。クレタ島出身のエピメニデスが「クレタ人はみな嘘つきだ」と述べたという命題の真偽を問う際、クレタ人であるエピメニデスが真実を述べているとすると、クレタ人はみな嘘つきになり、嘘を述べていたとすると、クレタ人はみな正直になり、発話の主体であるエピメニデスが正直ものか嘘つきかであることと矛盾する、という説。自己言及のパラドックスまたは嘘つきのパラドックスとして広く知られる。
今日は、ここからゲーデルまで行こうと思っていたのですが、すでに今文字数確かめたらちょうど5000文字になっている……。
すでに、ここまで読んでくれていない人が大半……。
( U_U)
ということで、Pythonしながら説明というアイディアだと毎回こういうことになりそうな予感……
別のやり方の方が良いのだろうか……。
また考えてみます。

