
SVMによるパタン認識
パタン認識とは、写真に写っているのがミカンなのかリンゴなのかを認識したり、男か女かを区別したり、手書き文字を認識したりすることである。
それを、データを用いた機械学習で行なう。
ニューラルネットワークはパタン認識の手法だが、それ以外にも手法がある。 暫く前までは、サポートベクターマシン(Support Vector Machine: SVM)が、パターン認識 の最強力の手法だと考えられていた。
この方法では、データを分析して、いくつかのグループに分けることによってパタン認識を行なう。
分析を行うには、まず、「特徴量の抽出」が必要だ。
人間が果物の写真を見てミカンだとかリンゴだと認識できるのは、色や形という特徴が重要であると認識し、その特徴にしたがって区別しているからである。
ところが、コンピュータに写真を見せると、背景に写っているものなど、別のものを学習してしまうこともある。
そうならないように、果物の写真から果物の部分だけを抜き出す。この作業を「 特徴抽出 」という。
さらに、色や形などの特徴を数値化して、学習データにする。
データの特徴は複数個の数値から成るので、空間の中の一点(ベクトル)として表わされる。これを特徴ベクトルと呼ぶ。
図1 2次元の場合のSVM
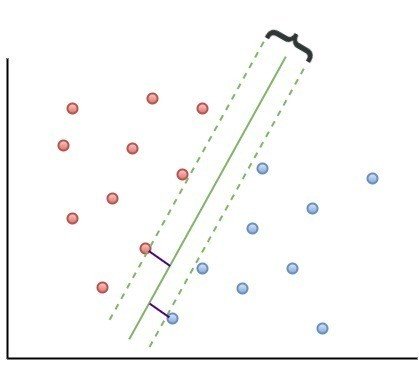
いま、2次元の特徴空間に、図1のようなデータがあったとする.
これらを、赤(リンゴ)と青(ミカン)で示す2つのグループに分類することを考える。
図1のように、2つの特徴を考慮して、緑色で示す直線で分けることが考えられる。
SVMでは、正しい直線(分類基準)を見出すために、「マージン最大化」という手法を使う。
これは、データの中で他のグループと最も近い位置にいるもの(これを「サポートベクトル」と呼ぶ)と境界を表わす直線との距離が最も大きくなるように、境界線を引くことだ。
これは、「マージン」という概念で表わされる。マージンとは、「境界とサポートベクトルとの距離」である。SVMは、「マージンを最大化する」(2つのグループの差異が最大になる)という基準で分類をしているのだ。
こうすると、「新しいデータが入ってきたときに誤判定してしまう」というミスを少なくすることができる。
図2 多次元の場合のSVM
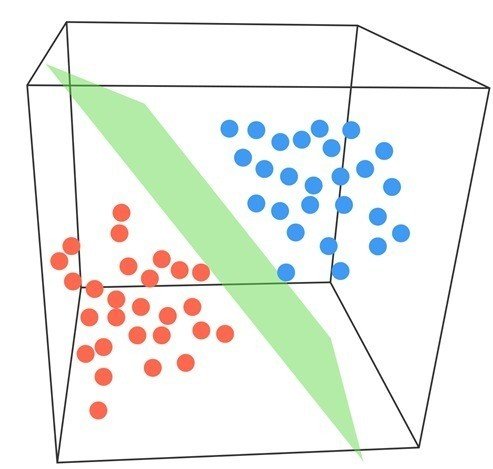
図1は、学習データは特徴ベクトルが2次元の場合だが、実際には多次元である場合が多い。その場合には、図2のような多次元空間で超平面による分割を行なう。
ところで、現実のデータには、図3のように、直線や平面で分割できない場合がある。
その場合には、「カーネルトリック」と呼ばれる手法を使う。
これは、特徴量を増やしたり、非線形の特徴量を利用することによってデータを分割する手法だ。

元のデータ空間から高次元空間にデータを写像し、その空間で、直線や平面による分割を行なうのだ。
この方法によって、SVMの適用可能範囲は大きく広がった。
なお、SVMは、通常言われる意味でのパタン認識以外にも利用できる。例えば、スパムメールの検出、不正取引の検出などにも利用できる。
