
【Data analytics】p値とどう付き合っていくべきか(part1)
0. 本記事のスコープ
part1では、p値の問題点を提起した上で、p値はどのような特徴を持っているのか確かめます。p値以外のアプローチについては、次回以降(part2)の記事で述べる予定です。
1. p値に関する問題点 ー思ったよりも簡単にp値ハッキングができるー
研究やビジネスの意思決定において、p値のハッキング(p値が設定した有意水準を下回るように操作すること)が問題となっています。
その問題点に触れている記事を3つ紹介します。
まずはTJOさんの記事です。
「p < 0.05でなければ受け入れられない」というカルチャーがもたらす弊害は非常に大きいわけです。ある時はfile-drawer effect*1につながったり、ある時はp-value hacking*2やdata dredging*3につながったり、と「データから真に意義ある知見を得る」という本義に悖る事態になることもある。
次にエナゴ学術英語アカデミーさんの記事です。
ひとつは研究者が低いP値を出そうと調整し続けた場合に起こる「overhacking」。P値を低くして、結果により説得力を持たせようと、0.05以下になってもデータの操作を止めずに微調整を続けちゃうことね
最後に李さんの「p 値の是非を考える」の論文、および「Data colada」の記事から引用です。
ここ数年,経済学,心理学,生物学の論文では,p 値の分布は明らかに p 値が 0.05 に等しいところに, 明白な突起があることを示している.唯一のできる解釈は,p の値を故意に 0.05 以下に操作した論 文が沢山存在していることである.

以上の主張から、私はp値ハッキングが身近な問題であり、p値ハッキングに惑わされないリテラシーを持つべきだと思いました。
では、どのようにしてp値と正しく向き合っていくべきでしょうか?
次のパラグラフで触れてみます。
2. 何を知るべきか?
ずばり、「p値の限界を知ること」、「p値以外のアプローチを知ること」だと考えます。
The American Statisticianでは、研究のコンクルージョンやビジネス、ポリシーを決める際に、p値だけで結論を出すべきでないと述べています。
Scientific conclusions and business or policy decisions should not be based only on whether a p-value passes a specific threshold.
さらに、データサイエンティスト協会のスキルチェックでは、p値以外の具体的なアプローチを述べています。
p値だけでは仮説やモデルの正しさを評価できないことを理解し、p値以外のアプローチ(信頼区間、信用区間、ベイズファクターなど)と併せて透明性の高いデータ分析や結果の報告ができる
以上を踏まえると、「p値には限界があること」「意思決定のアプローチはp値以外にもあること」がなんとなくわかります。
では、実際に「p値はどのような特徴があるのか?」また「p値以外のアプローチをどのように実践するのか?」という、新たな疑問が出てくると思います。
次のパラグラフでは、前者のp値の特徴に焦点を当て、実際にCodingをしながら証明に挑戦してみます。
3. p値の特徴を確認する
p値の限界を知るひとつの方法として、今回はサンプルサイズの大小とp値の関係に着目してみます。
サンプルサイズの大小は、p値ハッキングに大きな影響を及ぼす一つの要素であることに違いないので、確認していきましょう。
今回はKaggleで提供されているOpen data(New York のAirbnbのゲストハウスデータで、文末のGithubに入れてます)を使います。
「ロケーションと宿泊費は独立性がない(つまり関係性がある)のか」をχ2検定を使って検証したいと思います。
仮説検定
帰無仮説:ロケーションと宿泊費に関係はない
対立仮説:ロケーションと宿泊費に関係がある
有意水準5%で検証
サンプルサイズの変更
1回目:1000
2回目:500
3回目:100(*)
4回目:10(*)
上記の条件で検定をしてみましょう。特にχ2値とp値に着目し、サンプルサイズを変えるとどのような変化があるか確認していきましょう。
*【補足:独立性の検定ができない2つのケース】
後でも確認いただきたいのですが、独立性の検定が適用できないケースが2つあります。
1つ目は、”期待度数で1未満があるケース”です。今回、3回目と4回目の検定は、1未満があるので、独立性の検定が適用できないことを意味します。
2つ目は、”サンプル内に母集団で想定されるカテゴリが含まれていないケース”です。もう少し説明すると、4回目の検定では、Manhattan, Bronx, Staten Islandが含まれていないことが、2つ目のケースの一例です。
今回はサンプルサイズとp値を確認することが主旨のため、そのまま検定しています。
1回目:独立性の検定(n=1000)


2回目:独立性の検定(n=500)


3回目:独立性の検定(n=100)・・・*本当は独立性の検定ができない

4回目:独立性の検定(n=10)・・・*本当は独立性の検定ができない


サンプルサイズごとのカイ二乗値およびp値の関係

以上から確認できるように、サンプルサイズが大きくなるほど、χ2値は大きくなる傾向があり、その結果p値も有意水準を下回る可能性が高くなります。
4. 次回以降試したいこと
p値とうまく向き合っていくために、「p値の特徴を知る」と「p値以外のアプローチを知る」と推奨し、本記事では前者に着目しました。
ここまでは、p値がサンプルサイズに依存していることがわかったと思います。しかし、ビジネスでDecision makingする際は、どのようなアプローチが必要か知らなければなりません。
次回以降の記事で、p値以外のアプローチ(信頼区間、信用区間、ベイズファクターなど)にトライしたいと思います。
5. 参考資料
p値ハッキングとは何?
独立性の検定が適用できないケースはいつ?
p値以外のアプローチとは何?
スクリプトおよびデータ
6. コード
pip install scipy
# import
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# read csv
df_AB_NYC = pd.read_csv("AB_NYC_2019.csv")
df_AB_NYC.head()
df_AB_NYC.describe()
#”中央値(median)より大きい値”と”中央値以下”に分けて検証する
price_median = df_AB_NYC["price"].median()
# Build flag(0 or 1) for test
df_AB_NYC["price_flg"] = 0
df_AB_NYC.loc[(df_AB_NYC['price']>price_median),"price_flg"]=1
df_AB_NYC
## 答えたい問い(1):ロケーションと価格は独立性がない(関連性がある)と言えるか?
## サンプルサイズ大(n=1000)で実験
sample_1000 = df_AB_NYC.sample(n=1000)
#Make a Crosstable
table_location_price = pd.crosstab(sample_1000['neighbourhood_group'], sample_1000['price_flg'])
table_location_price
chi2, p, dof, exp = stats.chi2_contingency(table_location_price,correction=False)
print("期待度数:", exp)
print("自由度:", dof)
print("カイ二乗値:", chi2)
print("p値:", p)
## サンプルサイズ大(n=500)で実験
sample_500 = df_AB_NYC.sample(n=500)
#Make a Crosstable
table_location_price = pd.crosstab(sample_500['neighbourhood_group'], sample_500['price_flg'])
table_location_price
chi2, p, dof, exp = stats.chi2_contingency(table_location_price,correction=False)
print("期待度数:", exp)
print("自由度:", dof)
print("カイ二乗値:", chi2)
print("p値:", p)
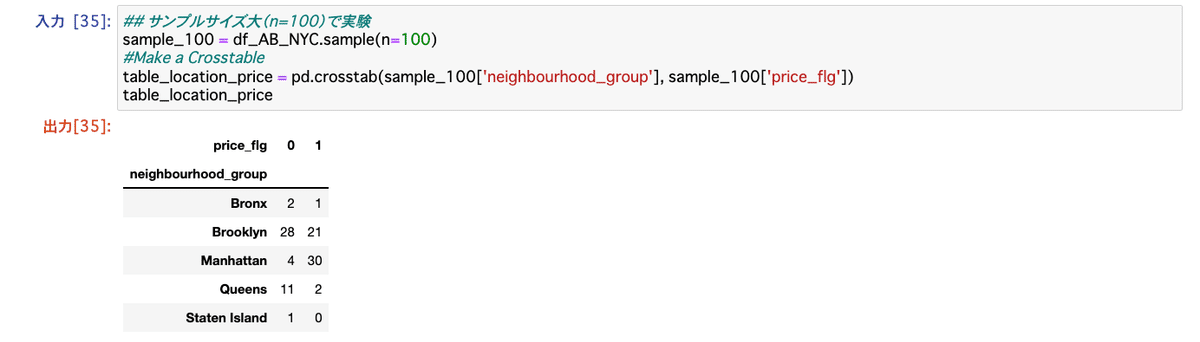
## サンプルサイズ大(n=100)で実験
sample_100 = df_AB_NYC.sample(n=100)
#Make a Crosstable
table_location_price = pd.crosstab(sample_100['neighbourhood_group'], sample_100['price_flg'])
table_location_price
chi2, p, dof, exp = stats.chi2_contingency(table_location_price,correction=False)
print("期待度数:", exp)
print("自由度:", dof)
print("カイ二乗値:", chi2)
print("p値:", p)
## サンプルサイズ大(n=10)で実験
sample_10 = df_AB_NYC.sample(n=10)
#Make a Crosstable
table_location_price = pd.crosstab(sample_10['neighbourhood_group'], sample_10['price_flg'])
table_location_price
chi2, p, dof, exp = stats.chi2_contingency(table_location_price,correction=False)
print("期待度数:", exp)
print("自由度:", dof)
print("カイ二乗値:", chi2)
print("p値:", p)
# カイ二乗値とp値を確認するための一覧表作成
tmp = pd.DataFrame({'x2_value': [111.94753844371967, 67.47695961875965,27.98556310917777,0.10416666666666667],
'p_value': [ 2.796249038106628e-23,7.733484160346962e-14,1.2557245867820693e-05,0.7468856333903637]},
index=["n=1000","n=500","n=100","n=10"])
tmp
(写真は2021年11月の上高地)
