
Microstrategyのネットワーク図可視化
たまに必要になったときに忘れてしまうので忘備録。MicroStrategyでネットワーク図の可視化表現機能があり、ちょっとデータの中身を確認したいときに便利なのですが、制約もあります。
ネットワーク図
ネットワーク図の表現は、ノード(点)と、エッジ(線)で表現されます。配置として、ノードが適切にばらけつつ、関連性のノード同士が近接しないとみずらくなってしまいます。これを適切に配置するアルゴリズムとして使われているものの一つが力学モデルです。igraphやnetworkxのようなライブラリーだとこれが実装されています。
Microstrategyでは3つの配置パターンが用意されています。1つは同一線上にノードを並べ、エッジを弧で描いて表現するパターン、もう1つはノードを円状に配置し、直線でエッジを表現するパターン、そして上述の力学モデルパターンです。特に最後のそれはデータをつっこめば直感的にわかりやすく配置されるので、大変重宝します。
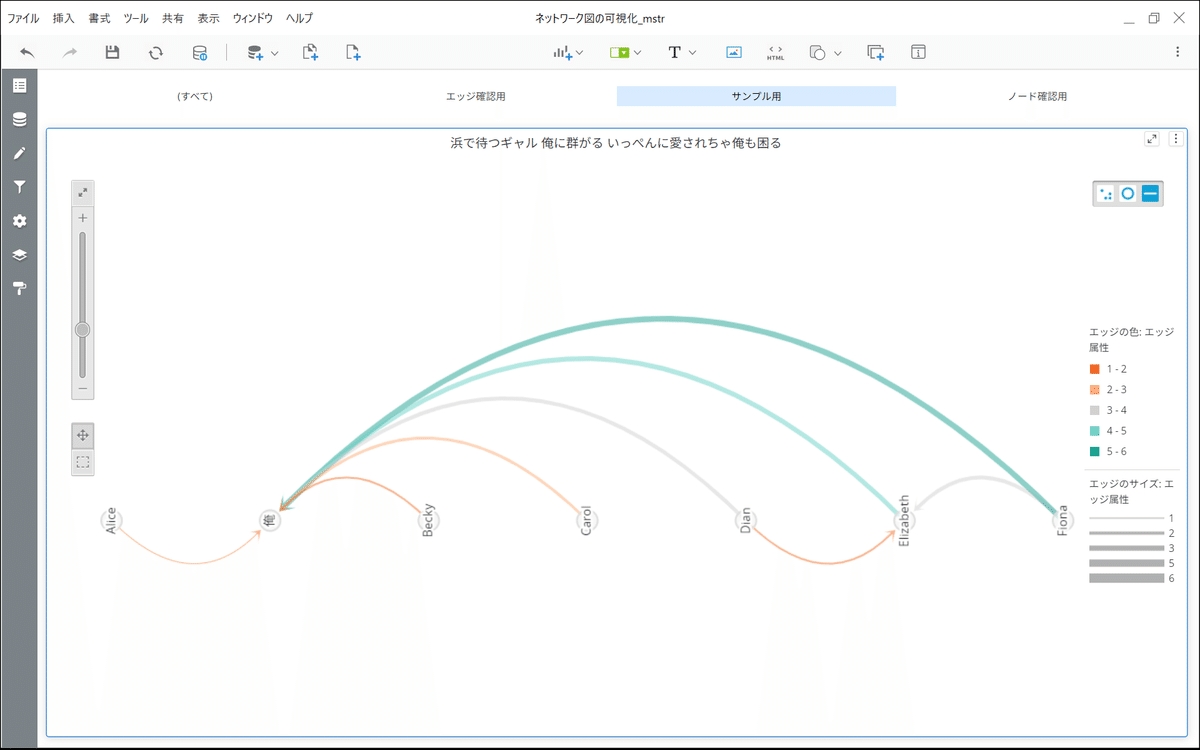


例えばigraphではノードの色とサイズ、エッジの色とサイズそれぞれにデータを割り当てて、ノードの大きさや特徴の違い、エッジの大きさや特徴の違いを表現できるのですが、Microstrategyではできることとできないことがあります。結論から言うとエッジの色とサイズは表現可能ですが、ノードの色は固定です。またノードのサイズに関してもちょっとどうなの?という実装で、分かって使わないと誤解を招きかねないです。というような話を以下につらつらと書きます。
データについて
以下のようなデータを用意しました。区分がサンプル用としているのは上述の例で利用したものです。以降ではエッジ確認用とノード確認用を使っていきます。
そもそもネットワークデータ、グラフデータと呼ばれるデータはどんな形をしているかというと、このような組み合わせ、ペアのデータです(縦横にノードを並べ、エッジの有無や量を行列内に表現することもあります)。ここではノードorigとノードdestがペアになります。そしてこのペア同士に方向がある場合と、方向がない場合があります。実際のデータで方向がある場合は、通話データや送金データ、電子メールのデータがわかりやすいでしょうか。AさんからBさんへとBさんからAさんへの架電が異なるケースです。これに対してソーシャルネットワークの友達状態は方向がない場合です。もちろん方向があるデータの方向を無視することもできます。
そしてこのノード、つまり点と点をつなぎ合わせるのがエッジ(線)です。この組み合わせ自体がエッジを示します。列としてどれという話ではなく、同じ行にノード同士が並ぶこと、それそのものがエッジデータです。
ノードとエッジそれぞれの特徴を表現しているのが、ノード属性、エッジ属性です。エッジ属性は各行に対して付与されるデータです。このデータはでは1列だけですが、複数列あっても構いません。例えば通話データなら通話回数と通話時間とかです。これに対してノード属性ですが、ノード自体がペアなので、両方のノードに関する属性を示しています。こちらもそれぞれに対して複数列あって構いません。加えて、一つのノードに対してある属性値がユニークである場合と、異なる場合が考えられます。今回は一つずつユニークです。例えば「Aliceの身長は160cmでユニークな値である」という場合と、「オイカワと括っていますがそれぞれ異なる個体であり、体長はそれぞれ16,15,14,17cm」といったユニークでない場合もあります。
エッジの確認
先に記したように、Microstrategyではエッジ、つまり線の太さと色を値に応じて変えることにより、つながりの強さ、関連性の強さを理解することが可能です。
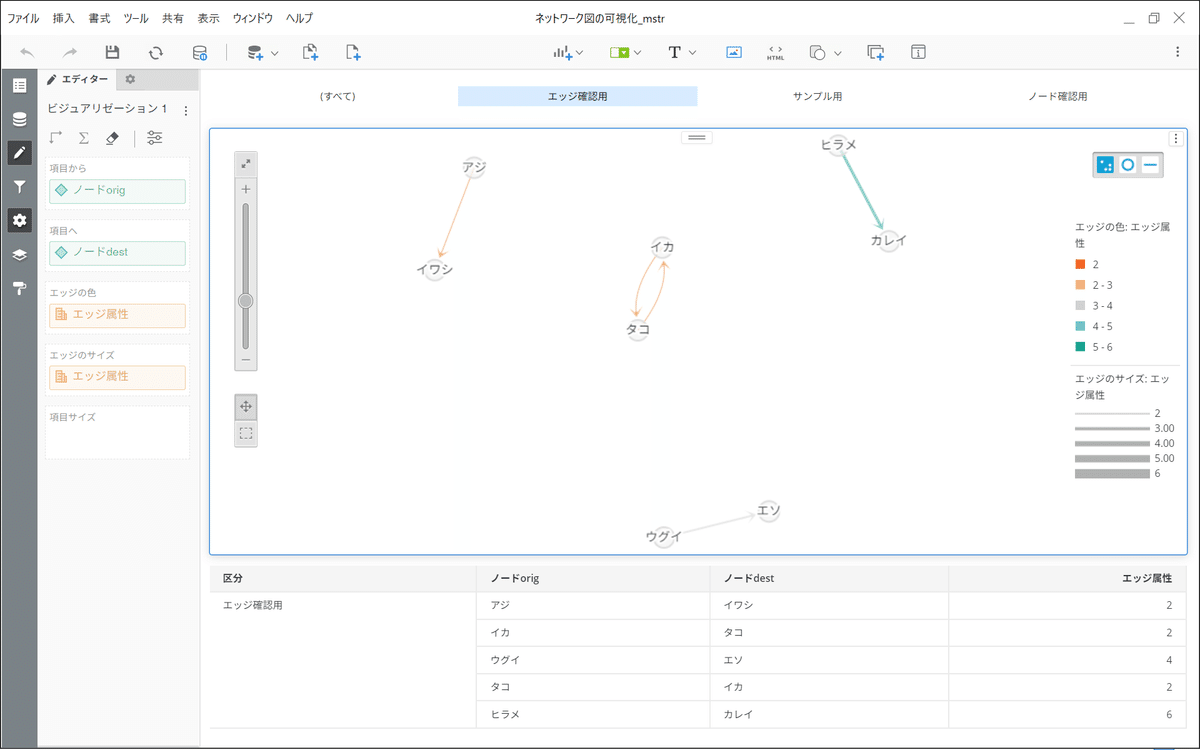
指標の使い方としては「項目から」、「項目へ」にそれぞれorigとdestのノードを指定し、エッジの色とサイズにエッジ属性を置いています。項目(ノード)サイズにはなにも入れていないため、ノード(点、丸)のサイズは固定のままです。今回は同じデータを利用したので、値が大きいほど緑が濃くなると同時に、線も太くなります。もちろんエッジの属性が2つあれば、それぞれに別の値をセットすることも可能です。
分かりやすいように下側にグリッドも表示させていますが、これを先に示した元データと見比べてみてください。アジとイワシの属性は2が1行、ウグイとエソの属性は2が2行ですが、こちらのウグイとエソはsumされて4が1行になっています。ここから、同一ペアの組み合わせはデフォルトでsumされることがわかります。
一方イカとタコです。ペアとしては同じなのですが、方向が異なるため(それぞれ反対の列に配置しているため)、弧を描いて両方がぶつからないように表示されています。つまりイカからタコのエッジと、タコからイカのそれは異なるものとして扱われます。
ノードの確認
次にノードの設定を見ていきましょう。ノードの色を値によって変えることはできません。固定の色に変更することは可能です。
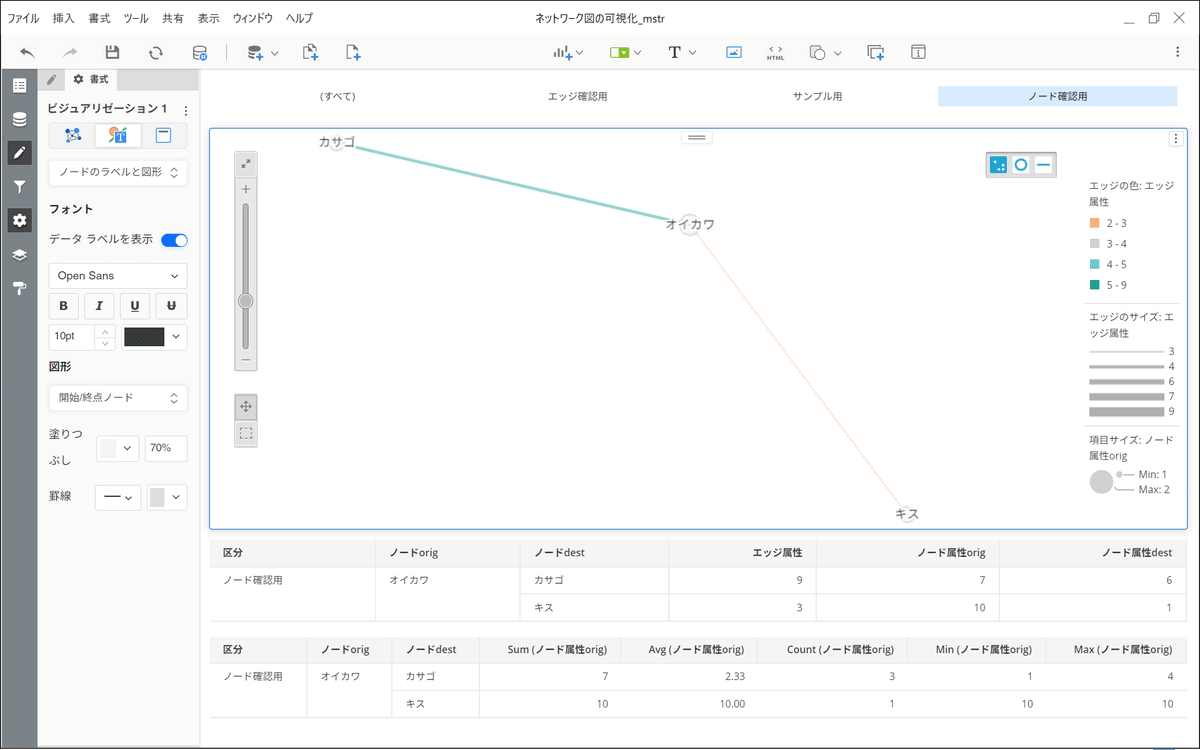
そしてノードのサイズですが、これが曲者です。設定としては「項目サイズ」(=ノードのサイズ)にノード属性を入れればよい、のですが、ノードはエッジの両端に存在します。どちらのノードを示しているのかという疑問がここで沸きます。色々見てみたのですが、ここで設定される項目サイズは、ノードの両端に対して適用されます。当然ながら両端のノード属性が同じでないことの方が多いため、ノードの属性を元にサイズを表現したい多くの場合、破綻します。一つだけ破綻しない場合もあるのでそれは追って記しますが、それ以外ではほとんど意図通りの表現はできないと思った方が現実的かと思います。
「項目サイズ」に入れた属性がどのように表現されるかですが、前述のように両端のノード表現に対して適用されます。そして各エッジ単位での内部集約、エッジをまたいだ外部集約を通じて、「項目サイズ」が決定されます。例を見ていきましょう。オイカワを例に先の元データを見ていきます。カサゴとつながっているのが3行、キスとつながっているのが1行です。一方で以下の図では、sum集約されています。今回はノード属性origを「項目サイズ」につっこみましたが、これとsum(ノード属性orig)が同じ値になっています。そしてcount(ノード属性orig)は元データの3行と1行を反映し、3と1になっています。これが内部集約です。
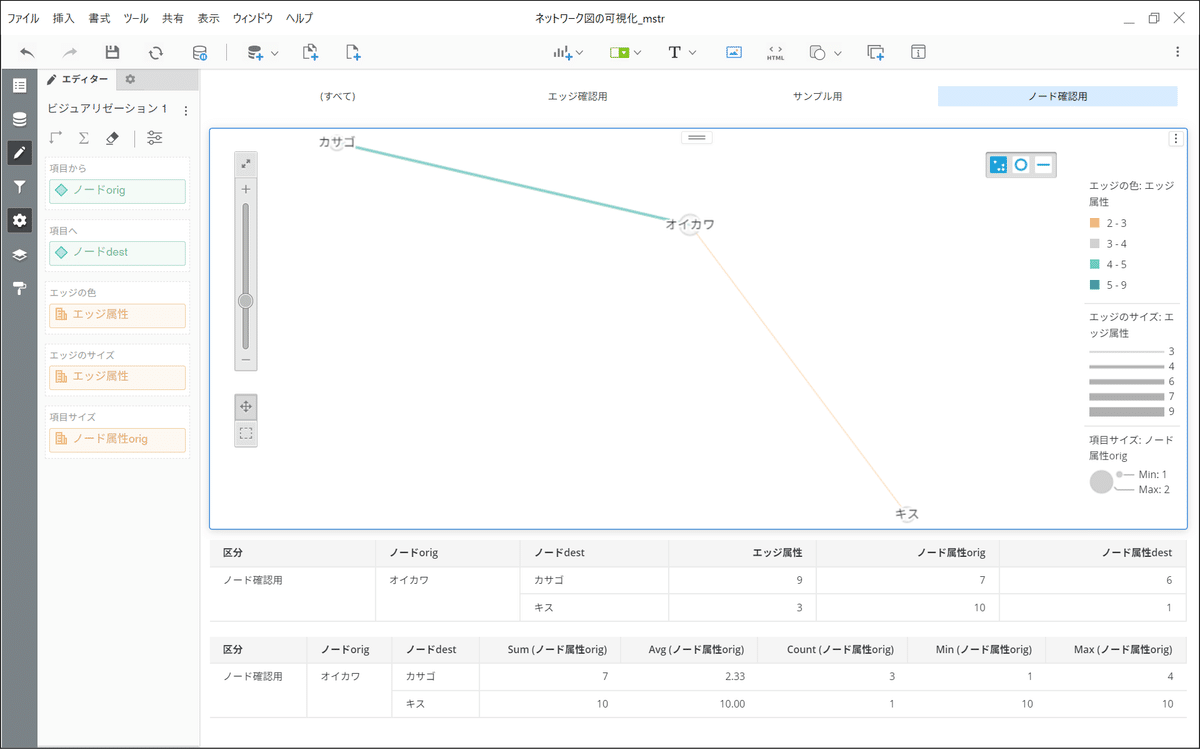
次に外部集約の話です。オイカワの「項目サイズ」は、カサゴとキスの両方とつながっているため、両方のつながりを考慮して決定されます。これを設定するのが[書式] > [サイズ集約]にて決定する集約方法です。
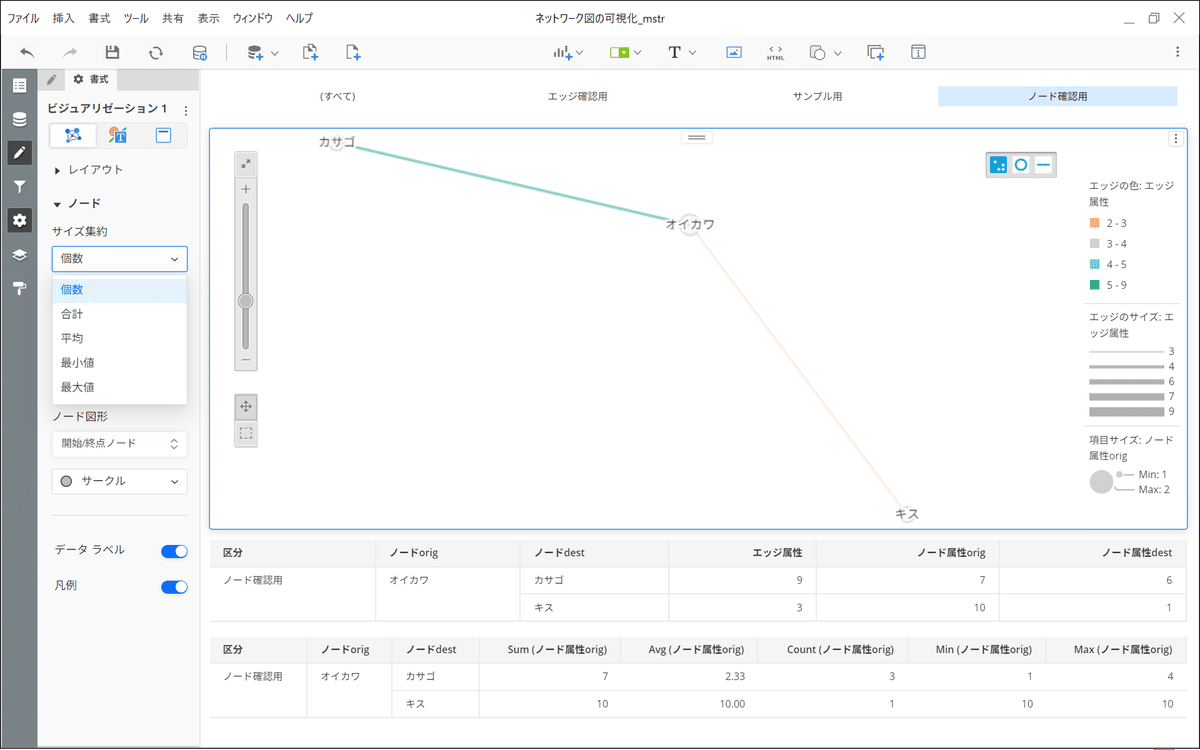
集約関数の選択肢としては内部集約同様、合計(sum)、個数(count)、平均(average)、最小(min)、最大(max)の5つがあります。そのため、内部集約と外部集約で5*5の集約バリエーションがあるということになります。つまり、外部集約関数(内部集約関数(ノード属性orig))がノードサイズの決定式です。ちなみに、明示的に集約を指定しない場合は、sum(sum(ノード属性orig))となります。以下にオイカワの場合における、集約バリエーションを示します。
以上が「項目サイズ」に関する解説ですが、そもそも両端のノードは異なりうるものであるのに、「項目サイズ」は両端のノードに関する属性であるとすると、ほとんどの集約バリエーションは何を示しているのか意味不明で、破綻しています。ただし唯一誤解なく、正しく表現できる指標があります。グラフ分析の世界ではdegree(次数)と呼ばれる指標で、ノードが他のいくつのノードとつながっているかをカウントアップする指標です。X(旧Twitter)であれば「フォロー数+フォロワー数-相互フォロー数」と考えていただけるとわかりやすいかと思います。その際の設定は簡単です。内部指標はなんでも良いので、とにかく外部指標を個数(count)にしてください。そうすると、それが表現したいものであるかは別にして、つながっているエッジの数を各ノードサイズに正確に反映できます。
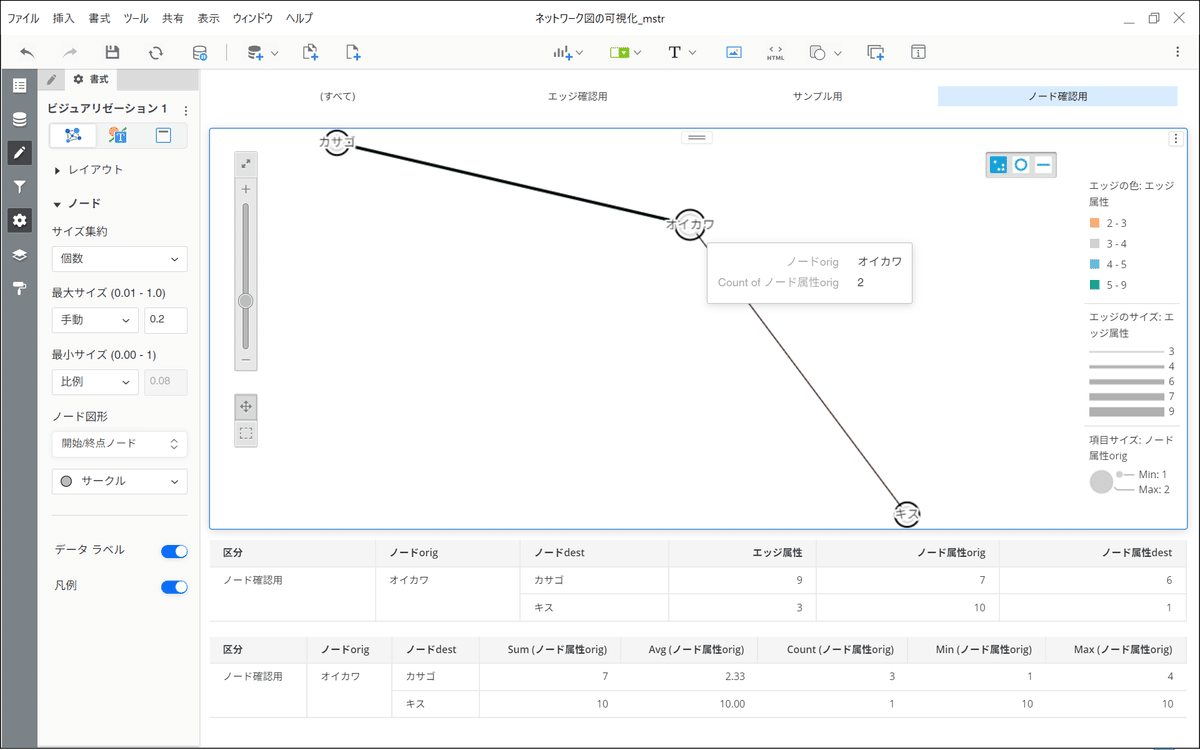
以上です。内々の確認で雰囲気を見たいときには、ほかの集約指標を使っても良いのですが、作った図表が独り歩きしうるとか、誤解を招いてはいけない場合には次数(=count(任意の集約関数(ノード属性orig)))を使うのが無難です。
