
位置情報とパブリックデータ#08: (地理空間関数)出現範囲ポリゴン化と数値型変換
(TeradataのSQL実行環境に関してはこちらをご覧ください)
例えば顧客の出現座標が複数得られ、特にその出現が何度も起こったとき、その出現場所は顧客が過去に出現した場所であると同時に、顧客がよく出現するであろう場所と理解できます。そのため、位置情報をベースとしたマーケティングを行う場合、顧客の行動範囲境界としてそれらの座標を利用できます。さらにこれらを点の集合ではなく、面として理解できれば、活用が容易になります。ここでは、複数の点を用いて、顧客行動範囲をポリゴンとして作成する過程を見ていきます。
また、ポリゴンデータを可視化する際に、そのままだと使いずらいため、これを点と順序のデータに変換して利用したいケースがあります。そのため、ここではポリゴンのデータを点の集合データとして変換する例も見ていきます。数値型の経度緯度情報の集合を面、つまりポリゴンにする手順と、反対に、ポリゴンとして保持しているデータを数値型の経度緯度情報の集合にする手順です。行ったり来たり。以下にノートブックをまとめましたが、データとしてはこんなデータを用意しました。
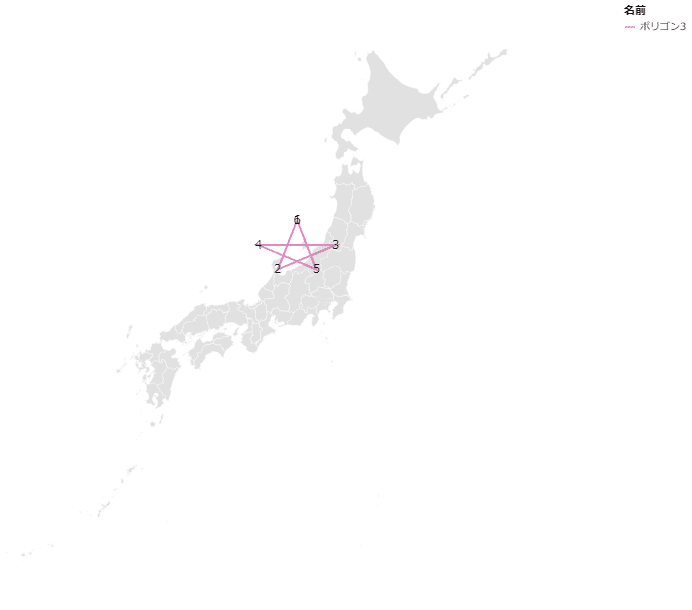
ある1名の顧客が出現したことを意味する経度緯度ポイントデータが5つ+1つあります。ダミーデータなので海洋上にも出現しています。このデータを使って行動範囲ポリゴンを作成したいのですが、出現時間順に線を引いたところ、ご覧のような星形になりました。本当はこれらの点を時計回りに並べ替えてポリゴンを作成できれば良いのですが、残念ながら順番はそうはなっておらず、星形になっています。ここでの課題は、時計回りに出現経度緯度のデータを並び替えてポリゴン化することです。
角度を利用した並び替え
出現データを時計回り(もしくは反時計回り)に並べなおすため、角度のデータを作成、利用しています。中心と各座標の位置関係を角度として捉え、角度の大きい順、小さい順で並び替えればそのまま期待する五角形になります。
処理の順序としてはまず、顧客ごとの出現座標の集合からその中心点を求めます。これは経度緯度それぞれの中心です。続いて、この中心から見たときの各座標の角度を求めます。角度は-180から180度であらわされ、この順番で並び替えます。そしてポリゴンなので始点と終点が同じ座標データである必要があることから、ちょっと工夫をしてポリゴンを閉じてあげます。最後に、縦に順序だって並んだ座標データを横につなげるため、npath関数を用いて単一カラムにします。余計な装飾などを整形してst_geometry型に変換したらポリゴン作成の完了です。
そして2点間の角度を求める方法ですが、以下の式で求めることができます。最初にatan2()、つまり逆正接(arctangent)を取得する関数で、ラジアン単位での角度を求めます。そしてこれをdegrees()、度数単位の-180から180の範囲で示される関数で、度数単位の角度に変換します。x2とy2は各出現経度と緯度を意味し、x1とy1は中心である基準座標の経度と緯度です。2つの距離差を入力としてラジアン単位の角度を求め、それを度数角度に変換しています。
degrees(atan2((x2-x1),(y2-y1)))
ポリゴンデータの分解と抽出
geometrytorowsという行に分解するテーブル関数を用います。onの中が入力データですが、2列で構成するのがルールです。最初の列は同じポリゴンオブジェクトであることを識別させるための列で、これは出口側のgeom_id1に出力されます。もう一つの列はst_geometry型の列で、ここにポリゴンがいます。マルチポリゴンの場合はそれぞれのポリゴンごとにelement_idが、単一ポリゴンの中に穴があるときにはそれぞれのサブポリゴンごとにring_idがセットされます。今回は使いませんが複雑なポリゴンを扱う際には識別情報として重要です。point_idはポリゴン内の出現順序を意味します。そしてxには経度、yには緯度が返されます。書き方がちょっと特殊ですが、こんなものだと思って使うのがよいかと思います。formatとして最後の列に指定するXは文字型で中の数字は文字数の長さ、Zは整数、99.99..は小数で桁数を指定しているようです。合わせてほかの記事で作成したバッファなどのデータも分解抽出しています。
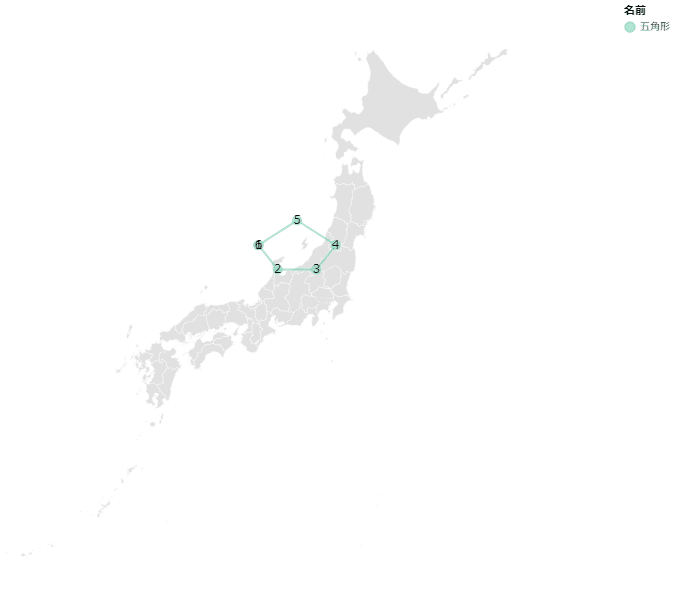
結果はこちら、期待通り五角形になっているのわかります。
グラフ描画時の定義jsonファイル、データのcsv/topojsonファイルを合わせて以下に置きます。
以上です。
#geospatial #gis #teradata #sql #analytics #st_geometry
