
3分で解ける?令和3年度都立高等学校入学者選抜学力検査問題(分割後期募集・全日制第二次募集)ー作図問題
令和3年度都立高等学校入学者選抜学力検査問題(分割後期募集・全日制第二次募集)の数学の問題です。
問題
解答欄に示した図をもとにして,頂点A,頂点B,頂点Cを全て通る円の中心Oを,定規とコンパスを用いて作図によって求め,中心Oの位置を示す文字Oも書け。ただし,作図に用いた線は消さないでおくこと。

解き方
頂点A,頂点B,頂点Cを全て通る円を描くためには,三角形ABCの重心を探せばよいです。
重心は次のようにして探すことができます。
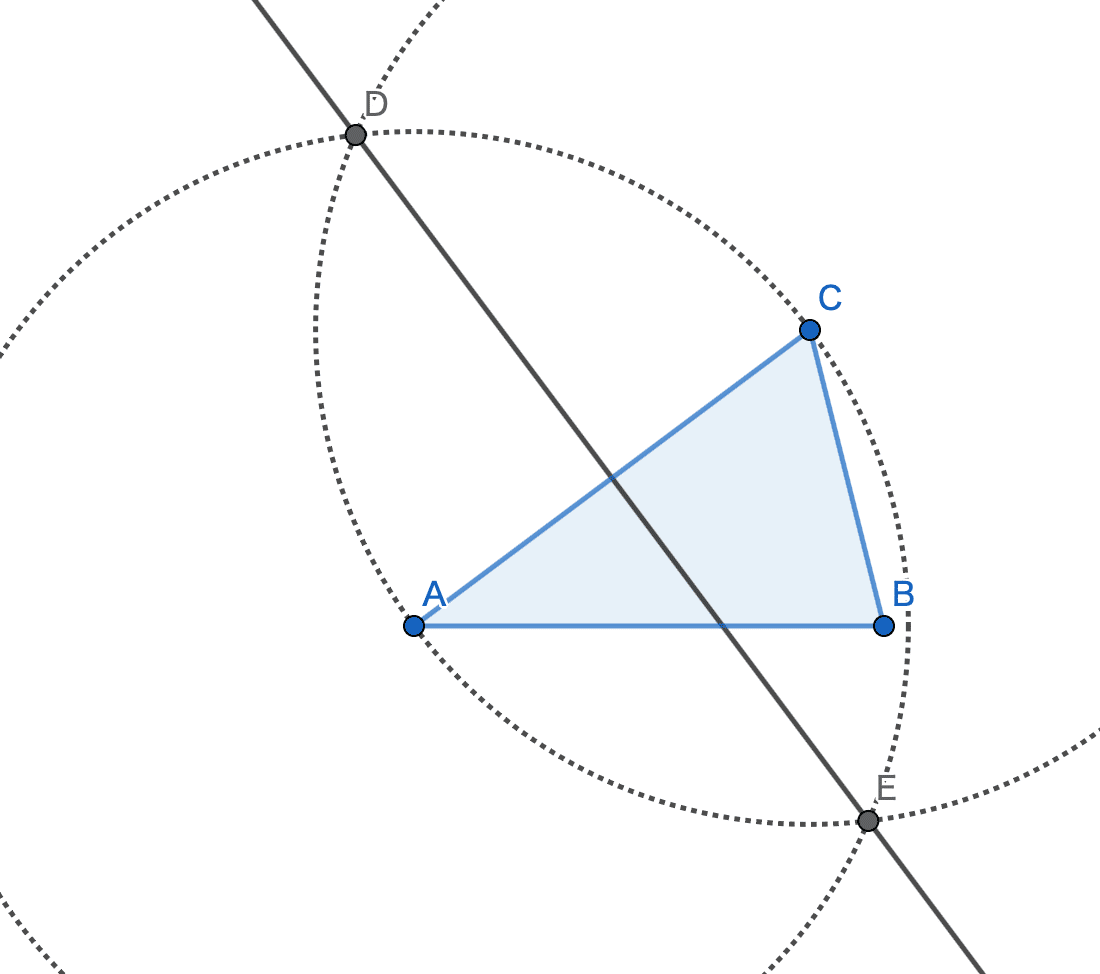
辺ACを二等分する二等分線を引く
辺ABを二等分する二等分線を引く
ふたつの二等分線の交点を点Oとする
1. 辺ACを二等分する二等分線を引く
辺ACを二等分する二等分線とは,辺ACを同じ長さに分け、その中点を求める線です。
「なぜ二等分線を引くのか」二等分線を引くことで、中心Oから頂点Aと点Bまでの距離が同じになる点を見つけることができます。これは、コンパスを使って、点Aを中心に半径OAの円を描き、同じ長さの半径で点Bを中心に円を描くと、2つの円は2つの点で交わるためです。この交点は、中心Oから頂点Aと点Bまでの距離が同じになる点です。二等分線を引くには、次の手順で行います。
点Aを中心に、適当な長さの円を描きます。
点Cを中心に、同じ長さの円を描きます。
円の交点を二等分線の始点と終点とします。
2. 辺ABを二等分する二等分線を引く
辺ABを二等分する二等分線を引くには、1. の作業を、辺ACの代わりに辺ABで行います。

3.ふたつの二等分線の交点を点Oとする
で引いた二つの二等分線の交点を点Oとします。
点Oを中心にOAを半径とする円を描くと、頂点A,頂点B,頂点Cを全て通る円を描くことができます。このように三角形の各頂点が円周上にある円のことを,外接円といいます。
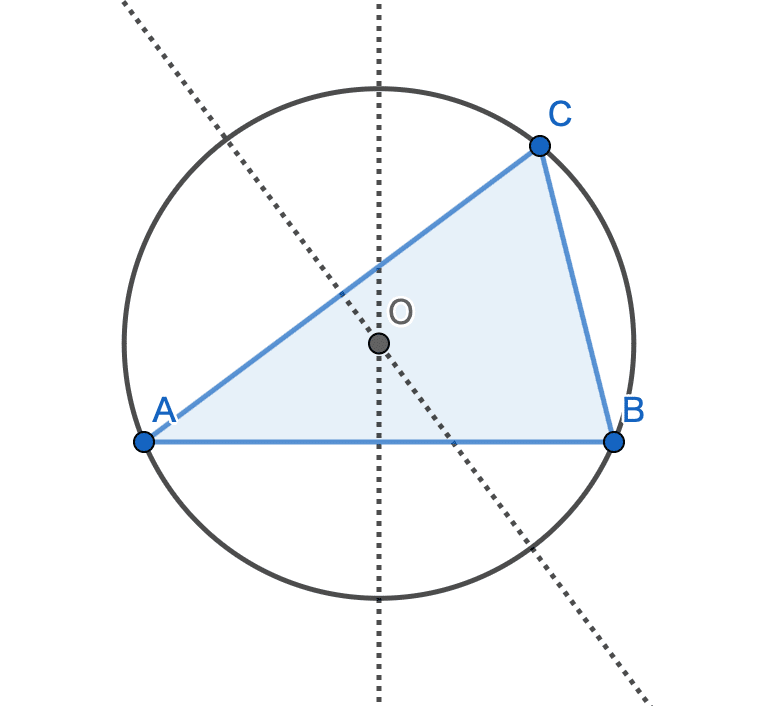
今回はわかりやすさを重視して,描いた円ふたつを消しています。実際の試験では描いた円は消してはいけません。
重点を中心にするとなぜ外接円が描けるのか
さて、なぜ以上のような手続きで点Oを見つけると、外接円が描けるのでしょうか。その答えは、なぜ二等分線を引くのかがわかればわかります。
三角形ABCの各頂点が円周上にある円。その中心点O。中心点Oと頂点A、B、Cはどのような関係にあるでしょうか。
中心Oから頂点A、B、Cまでの距離はすべて同じである
まずは、中心Oから頂点Aまでの距離と、中心Oから頂点Cまでの距離が同じになる点Oがどこにあるのか考えてみましょう。
コンパスを使って、点Aを中心に半径OAの円を描きます。同じ長さの半径で、点Cを中心に円を描きます。すると、2つの円は2つの点で交わります。この交点は、中心Oから頂点Aと点Cまでの距離が同じになる点です。

この点を通る直線を描くと、その直線上のすべての点は、中心Oから頂点Aと点Cまでの距離が同じになります。
同様の手順で、中心Oから頂点Aまでの距離と、中心Oから頂点Bまでの距離が同じになる点Oを見つけることができます。
したがって、2つの二等分線の交点は、中心Oから頂点A、B、Cまでの距離がすべて同じになる点であり、それは外接円の中心です。
