FFTの使い方と窓関数の必要性について
FETの使い方
FETは、時間軸を周波数軸へ変換してくれる演算です。
一定の時間間隔でサンプリングされた波形(時系列データ)を与えると、一定の周波数間隔で並んだデータ(周波数成分)が得られます。
FFT演算の答えは複素数(ベクトル)で得られ、そこから振幅や位相などを求めることが出来ます。
FFT演算を行うには(2のn乗)個のデータを与える必要があり、答えも同じ数だけのデータが得られます。
このFFT演算に与えたり、得られるデータの数(2のn乗)は、ポイント数と呼ばれます。

FFT演算から出てくる答え
FFT演算から出てくる答えは、一定の周波数間隔で並んでいますが、その間隔は周波数分解能(Δf)です。
Δfは、サンプリング周波数が(fs[Hz])、ポイント数が(Np)であれば、
Δf = fs[Hz] / Np [Hz]
と求められます。
FFT演算から出てくる答えは、FFTのポイント数(Np)個のデータですが、ほぼ真ん中で折り返し、同じ値が出てくるので、意味を持つのは約半分です。
最初のデータは(0Hz)、すなわちDC、直流成分で、つぎに(Δf)、(Δf×2)、(Δf×3)と続きます。
0から数えて(N/2)番目のデータが、サンプリング周波数の半分である、ナイキスト周波数[*]となります。
その後折り返して、ナイキスト周波数-(Δf)、ナイキスト周波数-(Δf×2)、ナイキスト周波数-(Δf×3)と続き、最後は(Δf)のデータで終わります。
直流成分とナイキスト周波数は1回しか出てこず、その他は2回出てきます。直流成分とナイキスト周波数はポイント数で割ると、その他はポイント数の半分で割るとレベルがそろいます。
[*]サンプリング周波数の半分、ナイキスト周波数は、離散的にサンプリングされたデータが、それ以上の周波数成分を含むことが出来ないことが知られています。

サンプリング周波数(fs)=64Hz、ポイント数(Np)=64として、実際に周波数を割り当てた例です。

窓関数の必要性
波形の区切られ方
FFT演算を行なうには、ちょうど(2のn乗)個のデータにしなくてはいけません。
そのためFFT演算を行なうには、連続的にサンプリングされた波形を、ちょうど(2のn乗)個のデータに切り出す必要があります。
つぎの図は、ちょうど2周期で波形が切り出せた場合ですが、いつもこのように、ちょうど波形の周期と同じ区切りで切り出せるとは限りません。

通常は波形の周期とは一致しない、どこか中途半端な場所で区切られていしまいます。
例えば2.5周期で区切られると、つぎのようになります。
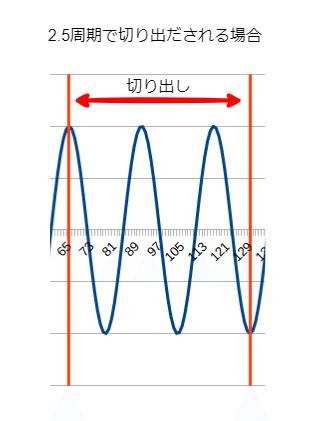
このようにして区切られた波形をFFT演算は、永遠の過去から、永遠の未来まで繰り返されるものとして答えを出します。
区切られた波形の前も、そのさらに前も、後ろについても同様に、同じ波形が繰り返されるものとして演算します。
つまりFFT演算はつぎのような波形だと思い込み、答えを出します。

これでは元の波形と違った波形になっています。
区切りのつなぎ目の垂直に切り立った部分には、元の波形にはない高い周波数成分が生まれてしまいます。

当然FFT演算を行なった結果はつぎのように、元の波形にはない高周波成分が現れてしまいます。
なお、FFT演算は区切った区間の1周期が最小分解能になり、その整数倍で答えが出てきます。
今回の2.5周期はその分解能の途中になります。その場合このように、隣接する成分に分散して答えを出します。

窓関数
データを区切ったつなぎ目で、高周波成分が発生しないように、通常はFFT演算を行なう前処理として窓関数が使われます。
窓関数にはいくつかの種類がありますが、大体このような形をしています。左右対称で真ん中は「1」、両端は「0」となります。

窓関数の演算は、元の波形との単純な掛け算です。このような形を掛けることで、区間の両端を「0」にもっていけます。

これをつなぎ合わせても、垂直に切り立った波形にはなりません。つなぎ目に発生する高周波成分をなくすことが出来ます。
窓関数は、元の波形の周波数成分は、できるだけ変えないように考えられています。

窓関数を掛けたあとでFFT演算を行なった結果を見てみましょう。
つぎのように高周波成分はなくなっています。
窓関数の影響で若干レベルが落ちます。周波数成分の特徴は損なわないようになっています。

このようにFFT演算では窓関数を用いることにより、データを(2のn乗)個で区切ることで発生する余計な高周波成分を取り除くことが出来ます。
