「星勘定」のためのツールー予選リーグ突破をシミュレーションする。「突破のホライゾン」
いよいよオリンピックだ。
様々な競技で予選リーグが始まるが、予選リーグの「星勘定」を行いたいとき、色々なパターンがあって、頭が混乱することがあるかもしれない。
そんなとき、あらゆるシチュエーションを一つのグラフにまとめられるとしたら、どうであろうか。私が使っているモデルをぜひ皆様に紹介したい。
「突破のためのホライゾン」というものである。
ここでは、近年で、最も思いだすことができるスポーツ・イベントということで、W杯2022年の予選リーグを例に説明させて頂きたい。
このとき、日本は、ドイツ、コスタリカ、スペインと同じグループであった。
まずは、グラフを説明したい。以下は、初期状態のグラフである。

直線は、勝点0を始点とし、勝点3が終点となるものである。
ざっくり、この直線上を勝点が移動すると考えていただければ良い。
初期状態であるので、必ず、0から始まり、負ければ0のまま、引分けたら勝点1上り、勝てば勝点3上るとなる。
では、試合の結果が分かったとき、どうすればいいのか。
下の図のように、始点(底)を上げるのである。具体的には、勝+3、引分+1のように。

さて、第1戦は、
ドイツ 1-2日本 勝点: ドイツ0、日本3
スペイン7-0コスタリカ 勝点:スペイン3、コスタリカ0
それをグラフにしたのが、下のものである

日本、スペインは、勝点+3ずつなので、直線の始点はそれぞれ3からとなる。
ドイツ、コスタリカは、勝点0なので、始点は0のままである。
これが、第1戦が終わったときの順位グラフである。
それでは、第2戦はどうなったか。
日本 0-1 コスタリカ 勝点: 日本0、コスタリカ3
スペイン1-1ドイツ 勝点:スペイン1、ドイツ1
それをグラフにしたのが、下のものである。日本は負けたので始点は3のまま、勝ったコスタリカの始点は3、ドイツとスペインは、引き分けたのでそれぞれ始点が1ずつ上がる。ドイツ1、スペイン4である。

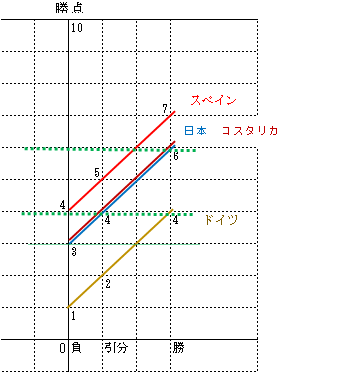
ここで、日本の予選突破のシミュレーションを行おう。
まずは、日本が負けた場合を考える。負けた場合、勝点+0なので、直線上を移動しない。そこで、この点を通る水平線を引く(下の緑の破線、これを「突破のためのホライゾン」と呼ぶ)

日本が負けた場合、スペインは勝つことになるので、勝点は7。日本の直線、スペインの直線を消去でき、スペインは勝点7の点、日本は勝点3の点に凝縮できる。
次に、日本の勝点3を通る水平線(「突破のホライゾン(水平線)」)を引き、水平線上の点、それより上の点を探すのである。を探すのである。
スペインは勝ったので、勝点7。コスタリカの勝点6、勝点4、勝点3。ドイツの勝点4。
これらをひとつずつ査定すれば、どのシチュエーションでも日本の突破はないことが分かる。
余計ややこしくなったと思われる方がいるかもしれないが、文章にすると、ややこしいだけで、パッとグラフを書けば、一発ですぐに分かります。
(また、このときのリーグ戦は、結果次第では、1位のスペインが突破できず、最下位のドイツまで予選突破の可能性があったので、ややこしい説明になりましたが、大抵は、もう少し分かりやすいです。)
同様に、②引き分けた場合、③勝った場合をあげたので、興味がある方は、やってみてください。
以上、私の「突破のためのホライゾン」の紹介であったが、このモデルの優れているのは、どの国の立場においても、一つのグラフの中で、シュミレーションできることである。また、勝点計算の異なる競技(バスケ、バレーボール、ラグビー等)においても汎用性があるので、使ってみてください。
オリンピック中に、いずれかの競技でシミュレーションが必要なときは、私もしゃしゃり出て、グラフを作って説明しようと思っています。