
データを段階化すると相関係数にはどんな影響があるか
企業の人事やマーケティングなどを対象とした心理学的な研究において、関係を調べたい2つの変数のうち一方が連続値で、もう一方が段階(順序尺度)というケースは非常に多く見られます。例えば、知能検査の結果(連続値)と人事考課(段階)の関係や、値引率(連続値)と購入意向(段階)の関係など。
連続値と段階に対して普通に相関係数(ピアソンの積率相関)を計算した場合、どのような傾向があるのか、コンピュータ・シミュレーションを使って調べてみることにします。手順は次のとおりです。
・相関が0の2つの正規分布から1000人分のデータの組を取り出す(この時点ではデータは連続値)
・一方のデータを段階に変換する。段階数は50段階、20段階、7段階、5段階、3段階、2段階の6通りで、各段階の理論上の比率が同じになるように連続値を段階に変換する。
・連続値同士で計算した相関係数と、一方を段階に変換した後で計算した相関係数を比較する。
・上記のプロセスを300回繰り返す。
このようにして、2つの変数のうち、一方を段階にした時に、相関係数がどのように変化するのかを確認します。また、段階数の影響についても把握するために、段階数のバリエーションを用意しました。
段階数を50段階にした場合の結果が下の図です。横軸は連続値同士で計算した相関係数、縦軸は片方を段階化した場合の相関係数で、点の一つひとつはシミュレーション試行を表しています(点の数は300個)。
もし段階化の影響が全く無ければ、点は対角線上に一直線に並ぶはずですが、結果を見ると、そうはなっておらず、段階数が50でも、段階化の影響がある程度存在することがわかります。ただし、例えば横軸が0.00のあたりの縦軸方向のデータのばらつきを見ると、概ね0.00±0.0125程度の範囲に収まっていますから、実際的には無視できる範囲であると考えて良さそうです。

段階数が20の場合が下の図です。段階数が50の場合よりも縦軸方向のデータのばらつきが大きくなっていることがわかります。

段階数が7の場合は、さらに縦軸方向のデータのばらつきが大きくなります。ただし、段階数が20から7と約1/3になったことを考慮すると、変化の程度はそれほど大きくないとも言えそうです。
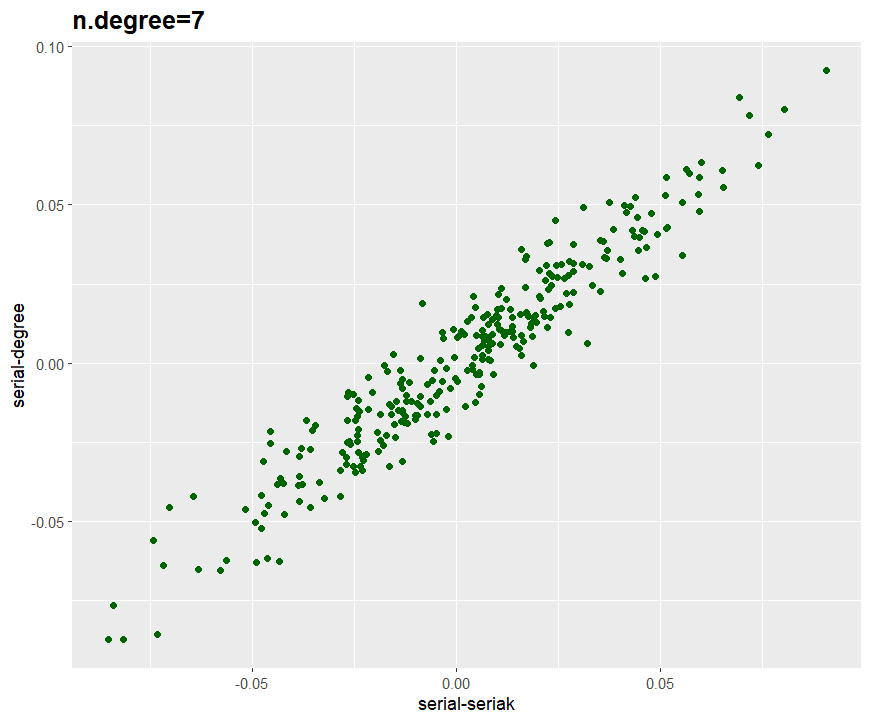
段階数が5になると、横軸の値が0.00の位置で縦軸が目視で0.00±0.025程度上下に変動するようです。段階数が多い場合と比較すると、段階化による結果の影響が大きくなって来ていることがわかります。ただし、この程度の影響であれば、実際の分析の結論が変わってしまうようなことはないとも言えます。今回の研究では、段階数が5程度あれば、そのまま相関係数を求めたとしても、実質的にはほとんど問題がないと考えて良さそうです。

段階数が3や2になると、さらに段階化の影響が大きくなります。この場合の影響も、通常イメージされるほど大きい訳ではないように見えますので、注意して解釈すれば「通常の相関を使うのはNG」というほどの問題ではないケースも多いと思います。


一方の変数が段階の場合の相関係数の特徴についてシミュレーションを使って検討した結果を見て来ました。
全体的な感触としては、段階数が5以上あれば、通常の相関係数を計算してもほとんど問題ないのではないか。段階数が3以下の場合には、結果が不安定であることを考慮した方がいいのではないかというのが個人的な感触です。
ただし、上記はシミュレーションに基づく検討の結果ですので、シミュレーションの設定の影響を受けています。また、相関係数の値の水準や結果の利用目的によっても判断は変わってくると思いますので注意してください。
これまで、数値を段階化すると、一般に『相関係数の絶対値は小さくなる傾向がある』というのが経験的な印象だったので、今回の結果は少し意外でした。連続値を段階化する際に各段階の出現率を一定にしましたが、もしかすると、このあたりのプロセスが実際とは少し異なっているのかもしれません。段階化の影響は、よく指摘されるポイントですので、引き続き検討したいと思います。
この記事が何かのお役に立てば幸いです。
