
Topological Overlap Matrix (TOM)の解釈
ざっくりTOMとは
Topological Overlap Matrixとは、ネットワーク解析において、そのネットワークの中である2つのノードがどれくらい似ているかを示すための指標です。たとえば、遺伝子の類似度をネットワーク解析で可視化したとき、遺伝子Aと遺伝子Bがどれくらい似ているかを調べたいときにこれを使います。値は0~1で、大きいほど似ていることになります。
TOMの式に登場する記号の説明
計算式は以下の通りです。
$$
TOM_{ij}=\frac{a_{ij}+\sum_u^n a_{iu}a_{uj}}{min(k_i k_j)+1-a_{ij}}
$$
丁寧に説明していきます。ネットワーク解析は各ノードの類似度に基づいてノードを繫げるものです。ここでの"類似度"とはピアソンの相関係数であったり、コサイン類似度であったり実験の目的や条件によって変わってきます。ここでは簡単のために類似度がある一定水準を越えたらすべて1(100%の一致)として扱い、それ以外は0(まったく似ていない)を類似度として採用します。例えば「相関係数が0.8以上」という水準を設けたとしたら、それを超えるものは全て相関係数1,それ以下のものは相関係数0として扱います。
それに基づいて計算されたのが$${a_{ij}}$$です。そのまま相関係数を表している場合もありますが、今回はある一定水準以上似ていたら1、それ以下は0として扱います。なのでネットワーク上で繋がっていたら$${a_{ij}=1}$$, 繋がっていなかったら$${a_{ij}=0}$$となります。
$${k_i}$$はそのノードが他のノードとどれだけつながっているかを表します。具体的には「$${k_i=\sum_j^n a_{ij}}$$」で計算され、類似度の総和であることが分かります。今回は類似度を1か0かにしているので、$${k_i}$$はあるノードと繋がっている他のノード数を表します。
$${min(k_i k_j)}$$はTOMを計算したい2つのノードのkを比較して、小さいほうを採用します。$${k_i=3, k_j=5}$$の場合、$${min(k_i k_j)}$$は3になります。
$${\sum_u^n a_{iu}a_{uj}}$$はあるノードuに対して、TOMを計算したい2つのノードそれぞれの類似度の積を全てのノードに対して計算して足したものになります。$${a_{iu}}$$はiとuの類似度、$${a_{uj}}$$はuとjの類似度で、その績を計算しているので上記のような解釈になります。今回の場合類似度は1か0なので、ともに1の場合、つまりuに対してiもjも結合している場合のみ1が加算されます。さらに言い換えれば、iとjが共通して結合しているノードの数を計算していることになります。ここの値が大きい、つまり共通して結合しているノードが多ければ2つのノードがより似ていると言えます。
TOMの式の解釈
まずは簡単な分子から。分子の式を改めて下に書きます。
$$
a_{ij}+\sum_u^n a_{iu}a_{uj}
$$
さきほど$${a_{ij}+\sum_u^n a_{iu}a_{uj}}$$の説明でこれがiとjが共通して結合しているノードの数を示すと説明しました。それに$${a_{ij}}$$が足されている形になっています。シグマの部分はiとjがuという他のノードと繋がっているかどうかを評価するだけのものだったので、iとj同士が繋がっているかどうかを見るために$${a_{ij}}$$を足す操作をしているわけです。
要約すると分子は「2つのノードの結合先がどれくらい重複しているか」を示します。結合先がたくさん重複していればそれだけ似ているノードであると言えますよね。
次に分母の式です。解釈自体がちょっと難しい(自分もこの解釈で正しいかどうかわからない)ので図を使いながら説明します。式を下に書いておきます。
$$
min(k_i k_j)+1+a_{ij}
$$
結論を言うと「2つのノードの類似度の理論上の最大値」を表します。具体例を通して理解を深めます。$${min(k_i k_j)}$$のkがそれぞれ3と5で、互いのノードが結合していない場合を考えます。Fig.1にそのイメージ図を示します。
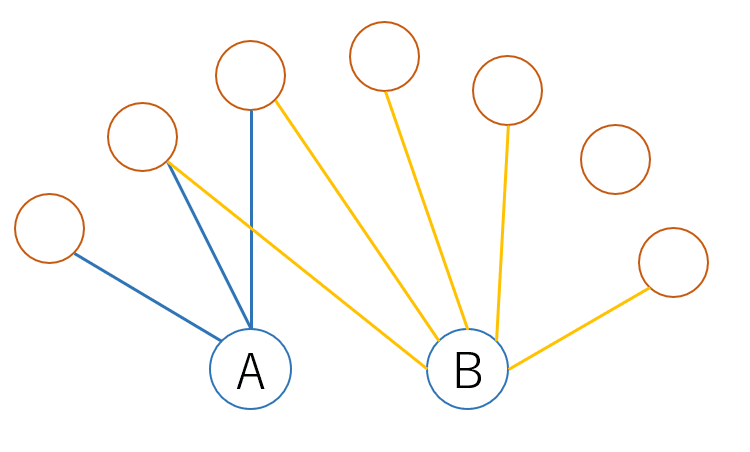
AとBのノードはそれぞれ3つと5つのノードと結合しています。このとき、A、Bがともに結合しているノードの数に注目します。ここでは2つ結合先が重複していますね。この重複数が多ければ多いほどAとBは似ていることになります。では、kがそれぞれ3と5の場合、この重複数の理論上の最大値はいくつになるのでしょうか。

Aの結合先は3つであり、この数以上の重複は考えられません。したがって、AとBの結合数のうち、小さいほうの数がそのまま理論上の最大値になります。つまり、このmin(k k)が「2つのノードの類似度の理論上の最大値」をそれとなく表しているわけです。なので式全体では「実際に重複している数/理論上の最大重複」になっており、これがトポロジー的な類似度を表していることは何となくわかると思います。
ここから議論をすすめなければいけないのは$${+1-a_{ij}}$$の項です。これについての正確な説明・文献が見当たらなかった(多分リサーチ不足)ため、自分なりの解釈を加えながら説明を進めます。結論を言うと、この項の存在で比較したい2つのノード同士が結びついている場合と結びついていない場合を区別できます。次のパートで使いたいので比較したい2つのノードが結びついている場合の図を貼っておきます。
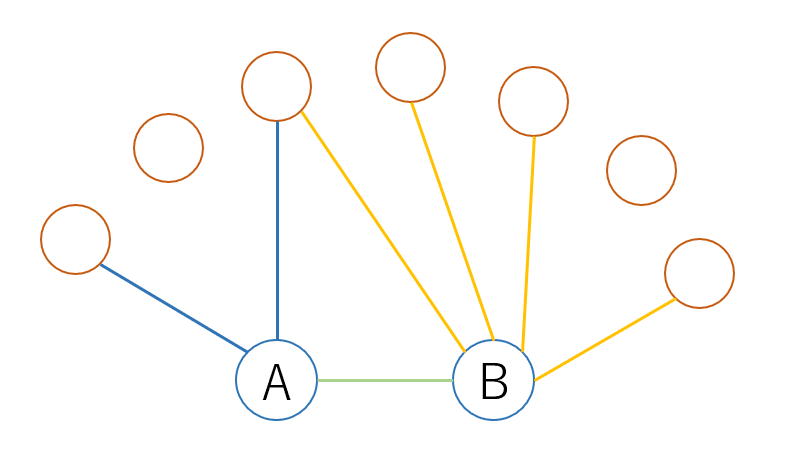
分母の式の解釈
ノード同士が結合していない場合と結合している場合について、先程用いていた具体例を使ってそれぞれ計算していきます。ただし、ここでは$${+1-a_{ij}}$$の項は無いものとして計算します。すると式は以下のようになります
$$
TOM_{ij}=\frac{a_{ij}+\sum_u^n a_{iu}a_{uj}}{min(k_i k_j)}
$$
ここにFig.1とFig.3の状況を代入すると
結合あり(Fig.3)の場合
$$
\frac{1+1}{3}=\frac{2}{3}
$$
結合なし(Fig.1)の場合
$$
\frac{0+2}{3}=\frac{2}{3}
$$
となり結果に差が出ません。そこで結合ありの値を変えずに結合なしの値を小さくする手法が必要になります。(結合ありの方を大きくしようとするとTOMの最大値が1を超えてしまう可能性があるので、比率を表す指標としては扱いにくくなってしまう)
まず分母に1を足すことで比率を小さくします。そして大きくなった分母から$${a_{ij}}$$を引き算することで$${a_{ij}}$$が大きい=類似度が高いときほど分母が小さくなるようにしています。今回は$${a_{ij}=1or0}$$なのでもう一度本来のTOMを計算すると
結合あり(Fig.3)の場合
$$
\frac{1+1}{3+1-1}=\frac{2}{3}
$$
結合なし(FIg.1)の場合
$$
\frac{0+2}{3+1-0}=\frac{1}{2}
$$
となって差を見出せるわけです。このような理由で分母に$${+1-a_{ij}}$$の項が挿入されているのではないかと考えます。あくまで僕の解釈ですが...
今回は簡単のために類似度を1か0にしましたが、もちろん”重み“を持たせた表現でも同じように計算ができます。
というわけでTOMの解釈でした。こういう数理モデルの解釈は楽しいですね。他にも数理モデルの解釈を記事にしていく予定なので是非ご覧ください。
