エンジニア実践的基礎: ヒープのプッシュ/ポップ

背景

このシリーズでは、エンジニアとして7年目を迎える節目に、これまで蓄積した知識を整理し、共有します。すべての記事を読めば、ミドルエンジニアとしてのスキルを身につけることができます。コンピュータサイエンスの理論よりも、実践的なソフトウェアエンジニアリングの知識に焦点を当てています。コーディングインタビューにも役立つ内容です。データ構造とアルゴリズムから設計、要件定義、バージョン管理、アジャイルなチーム開発、データベース、ネットワークなど、幅広いテーマを扱います。要するに、仕事に困らないレベルの知識を網羅します。

ヒープのプッシュ

前回に引き続きヒープの説明をします。今回はヒープのプッシュとポップです。前回同様に最小ヒープのみ説明します。プッシュもポップも最小ヒープの性質を常に満たすことが重要です。最小ヒープの性質は親ノードが子孫ノードより小さいこと、完全二分木であることでした。次のヒープに新しいノード 11 を追加するケースを考えます。

ノード 11 はどこに加えればいいでしょうか？完全二分木の性質を満たすには、常に左詰めなので、ノード 33 の右隣、ノード 24 の左子ノードとなります。

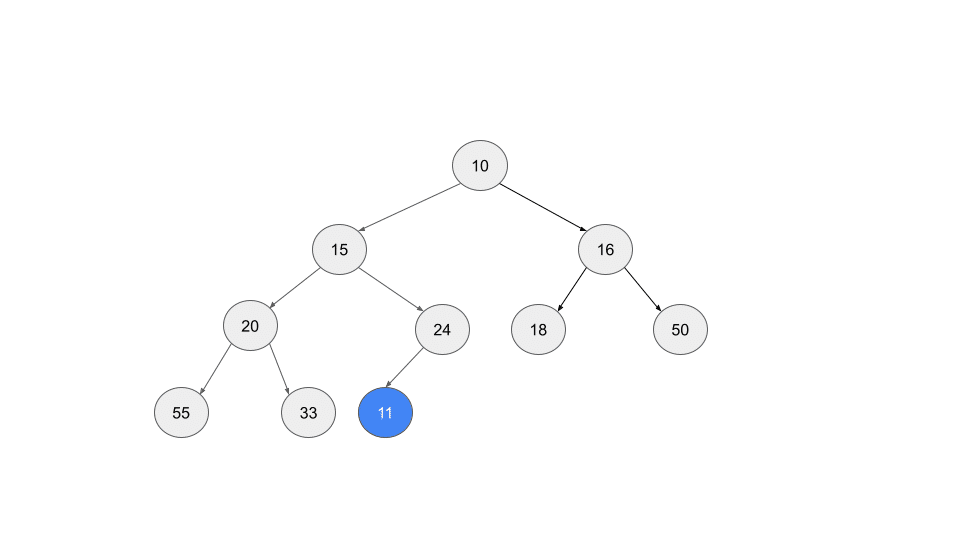
これで完全二分木の性質は満たしました。しかし、追加したノードが親ノードより小さい可能性があります。ノード 11 が親ノードより大きくなる地点を探します。まず、ノード 11 の親はノード 24 です。ノード 11 の方が小さいので入れ替えます。

親ノードが 15 に変わりました。ノード 11 の方が小さいので再び入れ替えます。

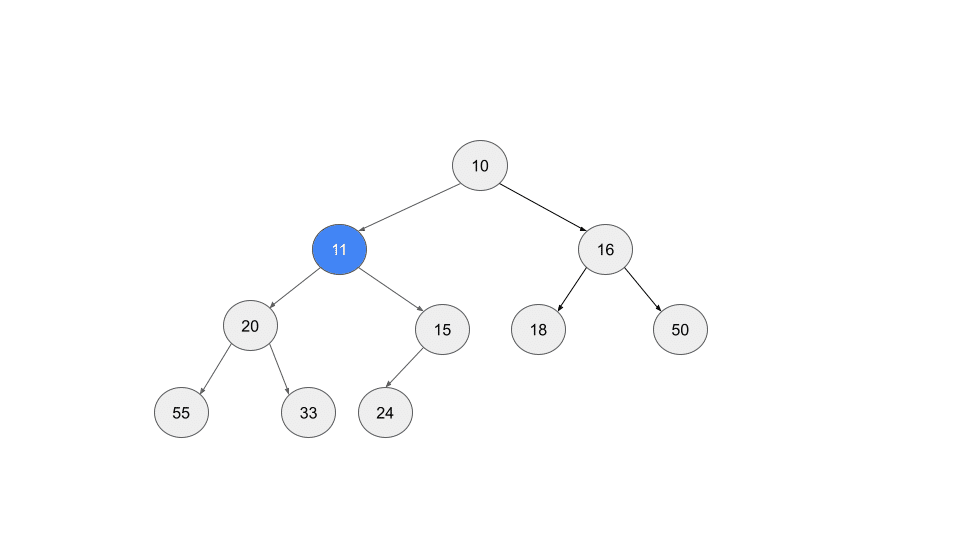
次の親ノード 10 はノード 11 より小さいので、これ以上交換できません。よってノード 11 の位置が確定します。親ノードが子孫ノードより小さいという性質が全てのノードで満たされていることが確認できます。

def push(self, val):
    self.heap.append(val)
    # 末尾に追加された追加ノードのインデックス
    i = len(self.heap) - 1

    # 追加ノードより小さいな親ノードを持つ位置を調べる
    # i > 1 はこれ以上は親ノードが存在しない = ルートノードに到達
    # i // 2 は親ノードのインデックスなので self.heap[i // 2] は親ノードの値
    # self.heap[i] < self.heap[i // 2] は親ノードより現在ノードが小さい
    while i > 1 and self.heap[i] < self.heap[i // 2]:
        # 親ノードと現在ノードを交換
        tmp = self.heap[i]
        self.heap[i] = self.heap[i // 2]
        self.heap[i // 2] = tmp
        # 現在ノードのインデックスを交換前の親ノードのインデックスに更新
        i = i // 2

ヒープのポップ

最小ヒープのポップは常に最小の値を取得できます。これが最小ヒープが他のデータ構造より優れた点です。しかしポップするとヒープの性質を満たさなくなります。ルートノードがなくなるので完全二分木ではなくなります。次のルートノードを残りのノードから探す必要がありますが、適当に配置すると子孫ノードより大きくなる可能性があります。ルートノード 10 をポップするケースを考えます。

とりあえず完全二分木の性質を満たしたいです。そこで末尾ノードである 33 をルートノードに移動します。

これで完全二分木の性質は満たせました。しかしノード33は子孫ノードより小さいでしょうか？左子ノードが 15 なので明かにこの性質を満たしていません。そこでノード 33 を左右子ノードと比較しながら、子孫ノードが全て自身より大きい位置を探します。まず右子ノードが存在するか確かめます。完全二分木の性質から左詰めでノードは追加されるため、右子ノードが存在するなら必ず左子ノードも存在します。次の左右子ノードのうちより小さい方を確認します。そして小さい方を現在ノードである 33 と比較します。もし左右子ノードのうち大きい方を現在ノードと交換すると、その時点で、より小さな子孫ノードができてしまうので、最小ヒープの性質を満たさなくなります。今回は左子ノード 15 と右子ノード 16 が存在し、左子ノード が右子ノードより小さいので、現在ノード 33 と比較します。左子ノード 15 は現在ノード 33 より小さいので、二つのノードを交換します。

同じ操作を繰り返します。今後も左右子ノードが存在し、左子ノード 20 は右子ノード 24 より小さいので、左子ノード 20 を現在ノード 33 と比較します。左子ノード 20 の方が小さいので交換します。

次の操作では右子ノードが存在しません。そのため自動的に左子ノードと現在ノードを比較します。左子のーど 55 は現在ノード 33 より大きいので、これ以上交換は不要です。これで全てのノードの子孫ノードが自身より大きくなったので、最小ヒープの性質を満たします。

def pop(self):
    # ヒープの第一インデックスはダミーなので長さが1ならポップするノードが存在しない
    if len(self.heap) == 1:
        return None
    # 長さが2ならポップするノードは1つしかない
    if len(self.heap) == 2:
        return self.heap.pop()

    res = self.heap[1]   
    # 末尾ノードをルートノードに移動
    self.heap[1] = self.heap.pop()
    i = 1
    # 左子ノードがある = リーフに到達していない限り継続
    while 2 * i < len(self.heap):
        if (
          # 右子ノードが存在
          2 * i + 1 < len(self.heap) and 
          # 右子ノードが左子ノードより小さい
　　　　        self.heap[2 * i + 1] < self.heap[2 * i] and 
          # 現在ノードより右子ノードが小さい
          self.heap[i] > self.heap[2 * i + 1]
        ):
            # 右子ノードを現在ノードと交換
            tmp = self.heap[i]
            self.heap[i] = self.heap[2 * i + 1]
            self.heap[2 * i + 1] = tmp
            i = 2 * i + 1
        # 左子ノードが現在ノードより小さい
        elif self.heap[i] > self.heap[2 * i]:
            # 左子ノードと現在ノードを交換
            tmp = self.heap[i]
            self.heap[i] = self.heap[2 * i]
            self.heap[2 * i] = tmp
            i = 2 * i
        else:
            # 子孫ノードは現在ノードより大きいのでこれ以上交換は不要
            break
    return res

計算量

値の取得はルートノードを参照するだけなので O(1) 。プッシュは半分ずつ配置箇所を探索するので O(log n)。ポップも半分ずつ配置箇所を探索するので O(log n)