エンジニア実践的基礎: BST の挿入と削除

背景

このシリーズでは、エンジニアとして7年目を迎える節目に、これまで蓄積した知識を整理し、共有します。すべての記事を読めば、ミドルエンジニアとしてのスキルを身につけることができます。コンピュータサイエンスの理論よりも、実践的なソフトウェアエンジニアリングの知識に焦点を当てています。コーディングインタビューにも役立つ内容です。データ構造とアルゴリズムから設計、要件定義、バージョン管理、アジャイルなチーム開発、データベース、ネットワークなど、幅広いテーマを扱います。要するに、仕事に困らないレベルの知識を網羅します。

BST の挿入と削除

BST の探索は探索範囲を半分ずつ狭めながら実行するものでした。ノードの挿入や削除も基本的な考えは同じです。挿入に比べて削除は少しトリッキーですが、少し考えれば納得できるはずです。

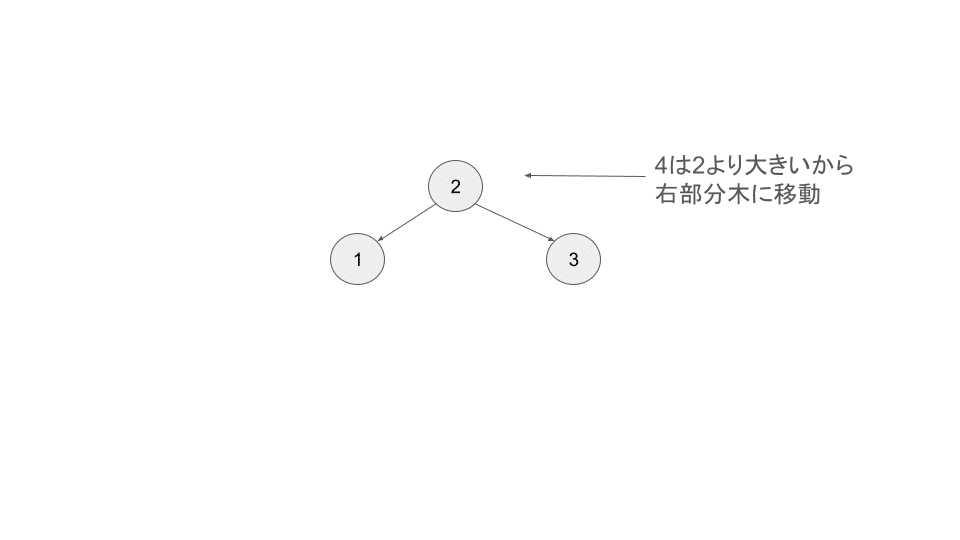
まず挿入は非常にシンプルです。探索同様にルートノードから開始して、挿入するノードが小さければ左に、大きければ右に移動し、再起的に繰り返します。そうするといずれはリーフノードに到達します。リーフノードは子ノードを持たないノードです。そのリーフノードより小さければ左子ノード、大きければ右子ノードとして追加します。4 を挿入する例で考えます。

def insert(root, val):
    if not root:
        return TreeNode(val)
    
    if val > root.val:
        root.right = insert(root.right, val)
    elif val < root.val:
        root.left = insert(root.left, val)
    return root

次に削除ですが、これは少し厄介です。まずは削除ノードを探索します。これは前回の内容です。次に二つのケースを考えます。

一つ目のケースは削除対象がリーフノードまたは子ノードを1つだけ持つ場合です。リーフノードであれば、ただ削除するだけで終了です。なぜなら子孫ノードがないので、ノードの移動が発生しないからです。子ノードを1つだけ持つ場合も簡単です。対象ノードを削除して、子ノードを上に移動させるだけです。例えば 1 はリーフノードなので自身を削除するだけです。BST は左子ノードが右子ノードより小さい必要があるので、移動するノードは右子ノードが優先されることに注意してください。

3を削除する場合は右子ノードの4を持つので、4を2に接続して元々3があった位置に移動します。

次は削除ノードが左右に子孫ノードを持つ場合です。単純に削除ノードを消して子ノードを上に移動すればいいと考えがちです。そうすると2つの疑問が出てきます。まず左右どちらのノードを上に移動するのか、そして移動するノードがさらに子孫ノードを持っていた場合どうするのか。

これらの問題を解決するには BST が守るべきルールに立ち返ります。BST はあるノードより小さいノードは左に、大きいノードは右に配置します。そのため、少なくとも削除ノードの位置には、左子ノードよりは大きく、右子ノードよりは小さいノードが配置されなければいけません。

要するに、そのようなノードを探索する方法がわかれば、それが解決策です。上の画像の例で考えると、5より大きく9より小さいノードは7です。このツリーは小さいので瞬時に見つけられますが、一つ一つ確認しなくとも、BST の特徴を利用すればすぐに見つけられます。

BST はノードの右側の部分木が常にそのノードより大きなノードだけで構成されます。そして、その部分木の最も左側のリーフノードは必ず、その部分木の中で最小値です。なぜなら小さな値は常に左側に挿入するからです。

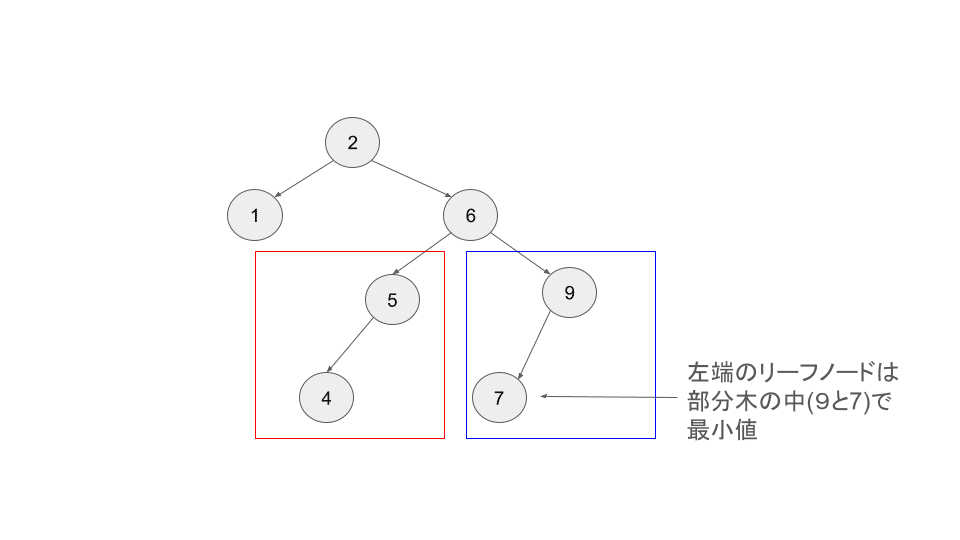
そのため、右部分木の左端のリーフノードを探索して、削除ノードの位置に移動すれば、BST の構成ルールを守ってツリーを再構築できます。

def minValueNode(root):
    curr = root
    while curr and curr.left:
        curr = curr.left
    return curr

def remove(root, val):
    if not root: # リーフに到達
        return None
    if val > root.val: # 右部分木探索
        root.right = remove(root.right, val)
    elif val < root.val:  # 左部分木探索
        root.left = remove(root.left, val)
    else: # 削除ノード発見
        if not root.left: # 右子ノード優先で移動する
            return root.right
        if not root.right:# 右子ノードがないなら左子ノードを移動する
            return root.left
        # 左右子ノードが存在するなら右部分木から最小値を取得して移動する
        minNode = minValueNode(root.right)
        root.val = minNode.val
        root.right = remove(root.right, minNode.val)
    return root

計算量

時間計算量: 平衡BSTでは挿入と削除は O(log n) 、非平衡BSTでは最悪の場合 O(n) です。

空間計算量: 最良の場合 O(log n) 、最悪の場合 O(n) です。再帰呼び出しがツリーの高さに比例するためです。