エンジニア実践的基礎: グラフ

背景

このシリーズでは、エンジニアとして7年目を迎える節目に、これまで蓄積した知識を整理し、共有します。すべての記事を読めば、ミドルエンジニアとしてのスキルを身につけることができます。コンピュータサイエンスの理論よりも、実践的なソフトウェアエンジニアリングの知識に焦点を当てています。コーディングインタビューにも役立つ内容です。データ構造とアルゴリズムから設計、要件定義、バージョン管理、アジャイルなチーム開発、データベース、ネットワークなど、幅広いテーマを扱います。要するに、仕事に困らないレベルの知識を網羅します。

グラフとは

グラフはノードとエッジでできたデータ構造です。実はすでにグラフについて学習しています。例えば木はグラフの一種で、閉路なしの連結グラフです。

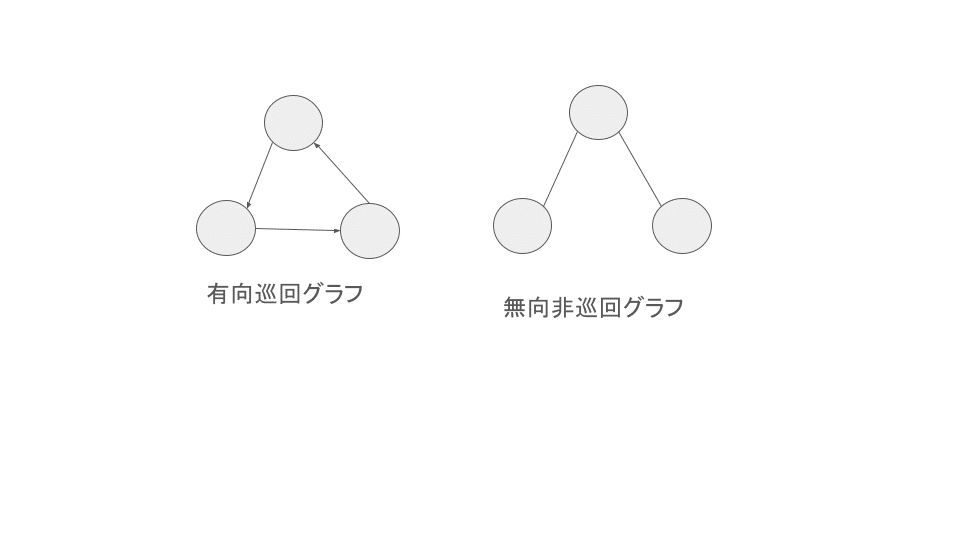
• グラフは矢印のように向きをもつ(有向)ものと持たないもの(無向)のものがあります。有向のエッジは一方通行で、向こうのエッジは双方通行です。

• グラフは複数の孤立した部分グラフから成り立つ場合もあります。どの2頂点も経路が存在する場合は連結グラフと呼ばれます。

• グラフは閉路を持つ場合も持たない場合もあります。閉路を持たないグラフは非巡回グラフと呼ばれます。

ノードの数(V)とエッジの数(E)は E ≦ V^2 という関係が成り立ちます。エッジはノードの数の2乗より多くはならないということです。

自分自身へのエッジも含む

グラフの表現方法には格子・隣接行列・隣接リストの3つがあります。

格子(Grid)

格子は二次元配列を 0 と 1 で埋めて、1がノードを表します。エッジはノードが隣接している箇所で表現します。

matrix = [[0, 1],
        [1, 1]]

隣接行列 (Adjacency Matrix)

隣接行列は格子同様に二次元配列を使用しますが、1 がノードではなくエッジを表します。

adjMatrix = [[0, 1, 0],
             [0, 0, 1],
             [0, 1, 0]]

隣接リスト(Adjacency List)

隣接リストは、全てのノードが隣接するノードの配列を持ちます。最も一般的なグラフ表現です。

class GraphNode:
    def __init__(self, val):
        self.val = val
        self.neighbors = []

node0 = GraphNode(0)
node1 = GraphNode(1)
node2 = GraphNode(2)

node0.neighbors.push(node1) # ノード0 -> ノード1
node1.neighbors.push(node2) # ノード1 -> ノード2
node2.neighbors.push(node1) # ノード2 -> ノード1

上記のコードを視覚化

空間計算量

それぞれのグラフ表現方法は実装だけでなく空間計算量も異なります。隣接リストが最もメモリ効率がいいです。

• 格子

  • 行(m)×列(n) 必要になるため O(m×n)

• 隣接行列

  • 行と列で同じ数のノード(V)が必要になるため O(V^2)

• 隣接リスト

  • ノード(V)と接続されるエッジだけ必要なので O(V+E)