エンジニア実践的基礎: ヒープ化
背景
このシリーズでは、エンジニアとして7年目を迎える節目に、これまで蓄積した知識を整理し、共有します。すべての記事を読めば、ミドルエンジニアとしてのスキルを身につけることができます。コンピュータサイエンスの理論よりも、実践的なソフトウェアエンジニアリングの知識に焦点を当てています。コーディングインタビューにも役立つ内容です。データ構造とアルゴリズムから設計、要件定義、バージョン管理、アジャイルなチーム開発、データベース、ネットワークなど、幅広いテーマを扱います。要するに、仕事に困らないレベルの知識を網羅します。
ヒープ化とは
ヒープとヒープのプッシュ/ポップと2回にわたりヒープの解説をしてきました。ヒープのプッシュの計算量は O(log n) なので、ノードが存在しない状態からヒープを構築すると O(n log n) の計算量になります。ヒープ化というアルゴリズムを使えば、O(n) でヒープを構築できます。次の完全二分木を見てみましょう。
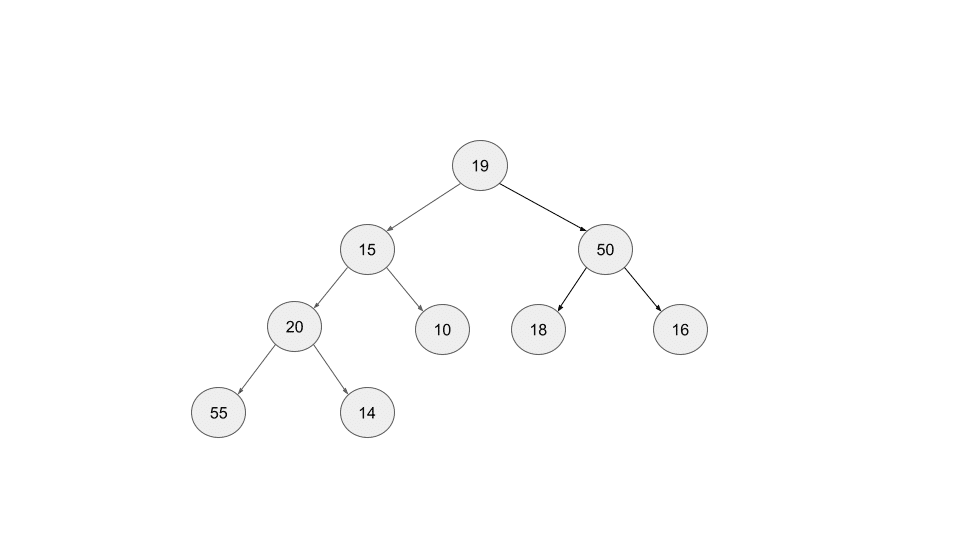
すでに完全二分木なので、残りの満たすべき性質は全てのノードの子孫ノードが現在ノード以下の値を持つことです。リーフから親ノードを比較しながら上がってもいいですが、リーフを持つ親ノードから初めても目的は達成できます。現在ノード(親ノード)より小さな子ノードを入れ替える処理をルートまで再帰的に繰り返します。この処理を子ノードを持つ全てのノードで実行します。







最終的に全ての親ノードが子ノードより小さい最小ヒープが完成します。
実装
def heapify(self, arr):
# 1番目の要素はダミーとして無視されるため1番目の要素を末尾にコピーする
# この時点で完全二分木の性質は満たされる
arr.append(arr[0])
self.heap = arr
cur = (len(self.heap) - 1) // 2
# 全ての親ノードが子ノードより小さくする
while cur > 0:
i = cur
while 2 * i < len(self.heap): # 子ノードが存在する限り繰り返す
if (2 * i + 1 < len(self.heap) and
self.heap[2 * i + 1] < self.heap[2 * i] and
self.heap[i] > self.heap[2 * i + 1]):
# 右子ノードと交換
tmp = self.heap[i]
self.heap[i] = self.heap[2 * i + 1]
self.heap[2 * i + 1] = tmp
i = 2 * i + 1
elif self.heap[i] > self.heap[2 * i]:
# 左子ノードと交換
tmp = self.heap[i]
self.heap[i] = self.heap[2 * i]
self.heap[2 * i] = tmp
i = 2 * i
else:
# 部分木がヒープの条件を満たす
break
# 次のノードに移動
cur -= 1
計算量
ヒープ化の時間計算量は O(n) であることが数学的に証明されます。ここでは数学を使わずに直感的な説明を試みます。ヒープ化はリーフノードを持つ親ノードから開始します。言い換えると、下から2つ目の階層からスタートします。完全二分木の性質上、下の階層ほどノードの数が多いです。そのため、ヒープ化の処理が多くなりそうですが、同時に、リーフに早く到達するため処理の回数はそれほどではありません。一方で上の階層に行くほど、階層に存在するノードの数は少なくなります。最終的に一つのルートノードに収束するからです。上の階層ではノードの数が少ない分、リーフに到達するまでの高さがあります。それだけ処理も多くなります。これらの処理回数を合わせておおよそで考えると O(n) になります。
