
方程式の眺め方の話~オームの法則を例にとって~
makersideでは、STEAM教育の中でもE=エンジニアリングに重きをおき、モノ・コトを創る過程でSTEAMの知恵を総合的に育んでいく取り組みの普及を推進しています
先日書いたこちらの記事で、特に説明もなく電気回路のオームの法則とか、微分方程式なんかにしれっと言及しました。
その中でも今回は、以前の記事に書いた以下のコメントについて補足を加えたいと思います。
オームの法則 V=IR から、抵抗にかかる電圧Vがわかれば、抵抗値を計算できます。
オームの法則V=IRというものがあったときに、この式をどういう風に見れば良いのか、どういう風に味わえばよいのかについて解説したいと思います。
物理学、電磁気学的なことを深堀する目的のものではないので、ご注意ください。
オームの法則の眺め方
オームの法則は「方程式」
物理学、電磁気学の話には触れないと言いつつも、さすがにV、I、Rの意味は補足しておきましょう。Vは電圧、Iは電流、Rは抵抗です。
「=」で左辺と右辺が結ばれているこの形式は、私たちが中学校に入ってほどなくして学ぶ「方程式」そのものです。
中学や高校の数学ではx,y、せいぜいzといった文字しか登場しませんが、別に方程式はx, y, zの文字を使わなくてはいけないというルールはありません。
左右の辺が「=」で結ばれていて、変数同士の関係を表していれば、それは方程式です。たとえば、「V=5」なんかは方程式とは言えません。
オームの法則の変数は3つ。2つの変数の値が確定すればもう1つがわかる。
オームの法則にはV, I, Rの3つの変数が含まれています。それに対していま、それらの関係を表す方程式としてV=IRという式が1つだけ与えられている状態です。
先ほどの引用に書いたとおり、電圧Vだけが具体的にわかった場合はどうでしょう。たとえばV=5とすれば、$${IR=5}$$ということになります。
これで、IとRは確定するでしょうか?
たとえばIが5のとき、Rは1になります。Iが2であれば、Rは2.5、Iが1であればRは5・・・IとRの組み合わせは無限に考えられます。
つまり、V=IRの関係において、V1つだけの値が具体的にわかったところで、残ったIとRは確定はしないのです。
「IとRを掛けたら一定値(IR=5)」という関係が導かれただけで、チェックメイトとはなりません。
いまは仮にVの値だけ分かった場合を例にとりましたが、試しに、IかRのどちらかだけの値がわかった場合についても考えてみるとすぐに、同じことだとわかるはずです。
つまり、未知数が3つあるときに、値が1つわかっただけでは残りの2つは確定しないということです。
ではV=5に加えて、I=2がわかった場合はどうでしょう。$${R=\frac{V}{I}=\frac{5}{2}=2.5}$$という風に、すべての変数の値が確定しますね?
未知数が3つあるときには、値が2つわからないと、全ての変数の値は確定しないということです。
一般的には、未知数がn個あるときには、値がn-1個わからないと、全ての変数の値は確定しないことになります。
さらに言うと、これまで「値がn-1個”わからないと”」と書きましたが、これは正確には「n個の未知数に関する関係式がn-1個与えられないと」となります。
先ほどの例では、V=5やI=2というのを「V, Iがわかった」と言うのではなく、「VとIに関する式が2つ与えられた」ということです。V=5もI=2も、VとIの関係式だということです。
IとRは反比例し、VとIまたはVとRは比例する
先ほどの$${IR=5}$$を、横軸にR、縦軸にIを取ってグラフを描くと、図1のような感じになります。

この関係を私たちは「反比例」として学んでいます。教科書では「$${xy=5}$$」だったり「$${y=\frac{5}{x}}$$」だったりしたと思いますが、xとyがただIとRに置き変わっただけで、同じことです。
Vではなくて、たとえば抵抗Rの値だけがわかっている場合はどうでしょう?R=5とします。そうすると、$${V=5I}$$となります。今度は、横軸に電流I、縦軸に電圧Vを取ってグラフを描くと、図2のような感じになります。
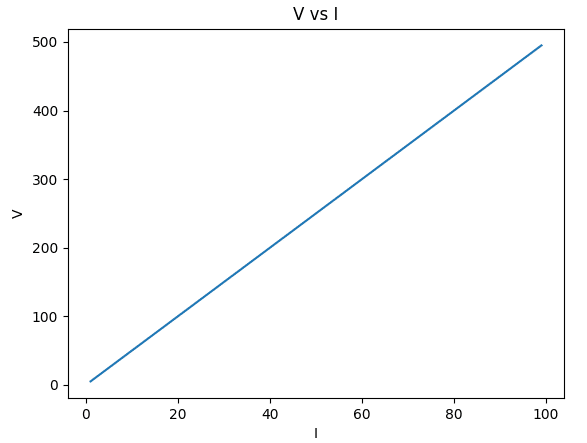
これも反比例とほぼ同じタイミングで学ぶ「比例」の関係ですね。教科書では「$${y=5x}$$」のように表現されていたと思いますが、xとyがただIとRに置き変わっただけで、同じことです。
VとI, Rの関係をまとめて図で表すと・・・
上の例では、VまたはRをそれぞれ一定値に固定した上での残り2変数の関係が表されていました。1変数を固定しないで、3者の関係をひとまとめにグラフで表すことはできるでしょうか。
すると、次の動画のような感じになります。一気に大学の雰囲気が出てきました。
要は、3つの変数の関係を表そうとすると、3次元グラフになるわけですね。動画の13秒くらいのあたりで直線のグラフ、20秒くらいのあたりで曲線が見えると思います。これがそれぞれ、先ほどみた比例と反比例のグラフに当たるものです。3次元のグラフで、どれか1つの変数を固定した断面を見ると、残り2変数の関係を表すグラフが見えてきます。
抵抗Rが死ぬほど大きかったら?
少しだけ電気の話に突っ込みますが、抵抗Rは電気の流れにくさを表すパラメータで、大きいほど電気が流れにくく、小さいほど電気が流れやすくなります。
金属では抵抗は小さく、絶縁物と呼ばれる電気を通さない物質では抵抗はバカでかくなります。
そういうわけで、もし絶縁物に電圧をかけたら何が起こるでしょう?
電圧はそこそこの値をかけて、抵抗がバカでかい。つまり、$${V=IR}$$で$${R→∞}$$だと何が起きるでしょう?
こう書くと大げさですが、$${I=\lim_{R\to \infty} \frac{V}{R}\simeq 0}$$となります。つまり、電流はほとんど流れませんねということです。極限の概念ですね。
このように、あるパラメータについて超極端なケースを想定する(メッチャ値を大きくor小さくしてみる)ことによって現象の振る舞いの基本的な傾向をつかむというのは、理系世界の常とう手段と言えます。
まとめ
オームの法則というシンプルな電気回路の法則を例にとって、方程式をどう眺めるかについていくつかの角度で見てみました。
左右の辺の式が「=」で結ばれていれば方程式
未知数がn個あれば、それらの関係式がn-1個与えられないとすべての値は確定しない
V=IRでは、IとRは反比例し、VとIまたはVとRは比例する
V=IRは変数が3つなので、3次元グラフで関係を表すこともできる
パラメータの超極端なケースを想定すると、現象の振る舞いの基本的な傾向をつかみやすい
