
一番わかりやすいROC曲線とAUCとC統計量
はじめに
「この検査値で生存と死亡のROC曲線を描くとAUCは0.89でした」みたいな説明を一度は学会で聞いたことがあるかと思います。しかし、実際その数字を聞いて、その検査値がどの程度患者のアウトカムを識別できているのかイメージできる臨床医はあまりいないのでは無いかと思います。
臨床研究、特に予測モデルの研究の論文を読むと頻出する、ROC曲線とAUC、C統計量という項目について解説し、これらがどのような特性を表しているのか解説したいと思います。
ROC曲線のAUCは検査の識別性能を表す
ROC曲線のAUC(Area under the curve)は「対象としている連続変数(例:検査の値、スコア、または予測確率)が、二値のアウトカム(例えば生存/死亡)をどの程度正確に識別できるか」を表しています。「識別?」と言われると今ひとつイメージが湧かないと思うので、これを図を用いて説明します。
ここでは、事例としてSOFAスコアみたいなスコアをイメージして説明します。SOFAスコアは敗血症患者の重症度を表すスコアです。0点から20点満点で、点が高いほど重症で死亡する確率が高いとされています。
このSOFAスコアが生存と死亡をどの程度正確に識別できるかを表すのに、「敗血症患者20人に対してSOFAスコアで生存・死亡に対するROC曲線を描くとAUCは0.88でした。」というふうに表現されて、下図のようにROC曲線が表されます。(この0.88は模擬データですので、実際の臨床における数字ではありません、念のため)
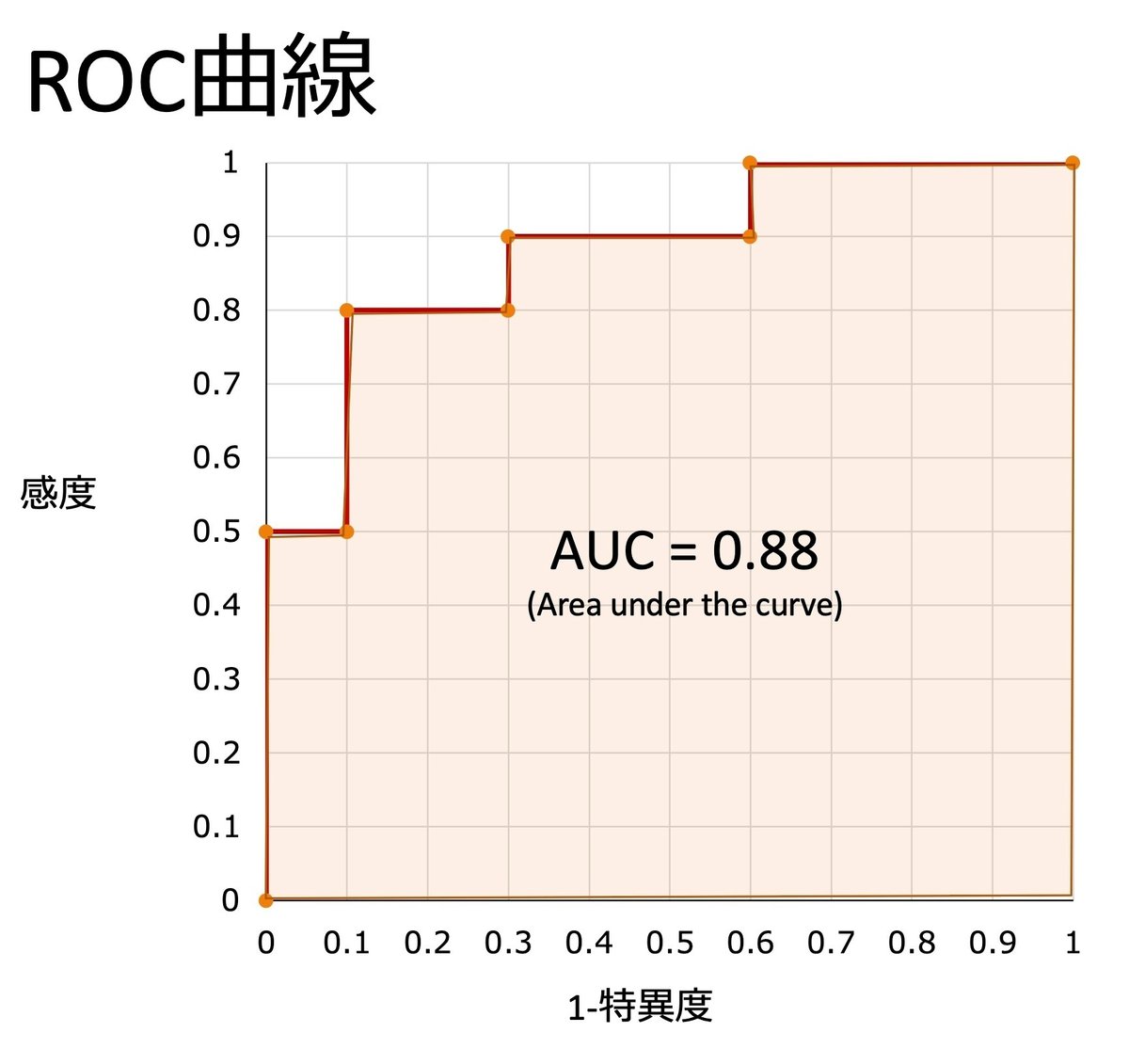
模擬データを使ってROC曲線を書いてみる
では、以下のような20人の患者さんのスコアとそれぞれのアウトカム(生存 or 死亡)の模擬データを用いてこのROC曲線を実際に書いてみます。

まずこの症患者20人をスコアで順番に一列に並べて図示します。

なんとなくスコアが高得点の人(列の右側)の方が「死亡」している人が多く、スコアの点が低い人(列の左側)の方が「生存」が多い感じです。なんだかこのスコアを使えば生存と死亡の識別に役立つかもしれません。
−1と0の間をカットオフにする

カットオフを決めて、そのカットオフより高い患者を陽性、低い患者を陰性とします。最初にカットオフをスコアの-1点と0点の間にします。(SOFAスコアはマイナス値はないので、便宜上です。)
この-1点/0点のところをカットオフにすると患者20人全員が陽性になります。この陽性患者20人のうち、10人が死亡、10人が生存です。2x2表を書くと上の図のようになり、感度は100%、特異度は0%です。
では、ROC曲線を書いてみます。x軸を1 - 特異度、y軸を感度と設定します。
感度は100%なので1.0、1 - 特異度は100% - 0%なので100% (=1.0)です。
なので(感度、1 - 特異度)=(1.0, 1.0)です。

5点と6点の間をカットオフにする
つぎに、スコア5点と6点の間をカットオフとして設定して、6点以上は「陽性」、5点以下は「陰性」とします。
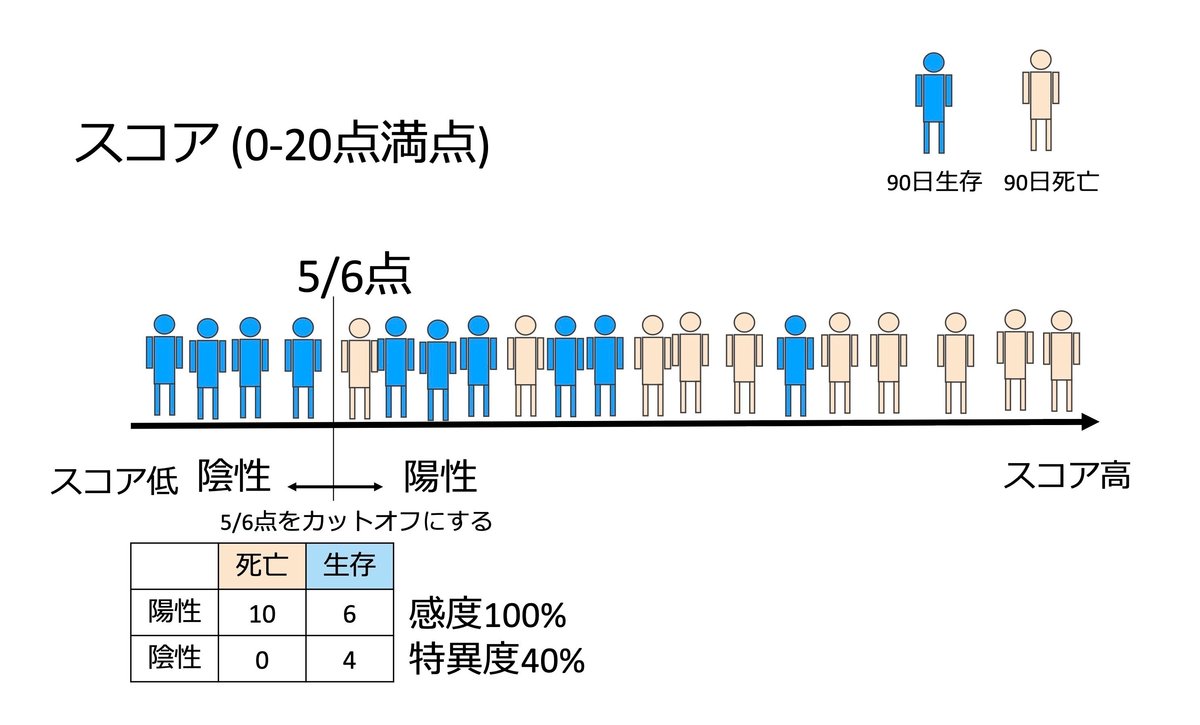
このときに、陽性・陰性と死亡・生存で2x2表を作ると上の図のようになり、感度:100%、特異度:40%となります。1-特異度は60%です。つまり(感度, 1 - 特異度)= (1.0, 0.6)となります。
これをプロットすると下の図のようになります。

6点と7点の間をカットオフにする
さらにカットオフを変化させスコアの6点と7点の間をカットオフにします。

この時、2x2表を書くと上の図のようになり、感度90%、特異度40% となります。 つまり、1-特異度は 60%となります。これをまたプロットすると以下のようになります。

同様に少しずつカットオフを変化させる
さらに下の図のように少しずつカットオフの値を動かしていくと、その都度、2x2表の数字が変わり感度と特異度が変化します。




このように少しずつカットオフを変化させていくと、その都度、感度と特異度が変化し、その点をプロットさせていくことで下のようなROC曲線が描けます。

この時のROC曲線の下の面積がAUC(Area under the curve)です。
このAUCの下のマス目を数えると88個です。100マスのうち88マスが曲線の下にあるのでAUCは0.88です。
完璧な識別?
ちなみに、下の図のようにAUCが1.0なら完璧な識別といわれます。一方、AUCが0.5なら検査結果はコインの表裏同様で偶然と変わらない、と言われますが、このAUC= 1.0と0.5の状況を考えます。

これを患者をスコアごとに一列に並べた図で表すと、以下のようになります。
AUC = 1.0のとき

つまりAUC=1.0の状況では、スコアを用いてあるカットオフを設定すると、生存と死亡が混ざり合うことなく、完璧に識別できる状態にあることを表しています。
AUC = 0.5のとき
一方で、AUC=0.5の状態を図に表します。

2x2表を書くと感度=1-特異度となる。
このような状況では、生存と死亡は均等に混ざり合い、どのようなカットオフを設定したとしても生存と死亡を分離、識別することができません。
ROC曲線とAUCの意味するところ
ここまでをまとめると、ROC曲線は連続変数の予測因子で患者を順番に一列に並べて、カットオフを変化させ、感度と特異度をプロットしたもので、検査値をもとに一列に並んでいる患者のうち、死亡と生存の患者(アウトカムの有無)をどの程度分離、識別できているかを表しているのがAUCです。
AUCから患者の分布を以下のようにイメージできるかとおもいます。

このようのAUCは検査値でアウトカムごとの患者の分布を表し、またそれがどの程度混ざり合っているかを検査値の順番によって表しているのが特徴です。
C統計量とは?
またC統計量という値もよく用いられます。
(理論上、C統計量はAUCと同じ値なります。)
C統計量は「アウトカムのイベントなし(生存)の患者とアウトカムのイベントあり(死亡)の患者を、ランダムに1人ずつ抽出した時に、それぞれの患者のスコアの大小関係が、(抽出した生存の患者のスコア)<(抽出した死亡の患者のスコア)となる確率」です。つまりこのスコアで適切に識別できている確率です。
上の説明をイメージ図で描くと、以下のようになります。

生存の患者のスコア<死亡の患者のスコアとなる確率がC統計量。
C統計量が0.5であればスコアが生存と死亡を識別できる確率は50%です。つまり偶然と同じです。一方で、C統計量が1.0なら、このスコアを用いれば生存と死亡を100%分離、識別することができます。この図をみるとC統計量がAUCと同じものを指しているのがイメージできると思います。
C統計量を計算してみる
ではC統計量を計算してみます。まずはAUC=1.0となるような状況を設定します。この場合、生存の人と死亡の人を抽出したときに、常に死亡の人の方がスコアが高いのでC統計量は1.0です。

では先ほど同じ、AUC=0.88となる状況です。スコアの点数で順番に並べます。スコアが低い方が生存が多く、スコアが高い方が死亡が多いです。

まず、スコアが一番低い死亡の患者(オレンジの矢印)が抽出された場合にに着目します。

このオレンジの矢印の患者よりスコアが低く生存しているのは4人です。つまり、生存した患者からランダムに一名抽出するときにこの4人が抽出された場合には(死亡の患者のスコア)>(生存の患者のスコア)となります。このような状況になるのは4/10=40%です。
同様に、別の死亡の患者に着目した場合、

このオレンジの矢印の患者よりスコアが低く、かつ生存しているのは7人です。つまり、生存した患者からランダムに一名抽出するときにこの7人が抽出された場合には(死亡の患者のスコア)>(生存の患者のスコア)となります。このような状況になるのは7/10=70%です。
また、以下の3人の死亡患者に着目します。

このオレンジの矢印の3人の患者よりスコアが低く、かつ生存しているのは9人です。つまり、生存した患者からランダムに1名抽出するときにこの9人が抽出された場合には(死亡の患者のスコア)>(生存の患者のスコア)となります。このような状況になるのは9/10=90%です。
このような感じで、確率を計算していきます。

それぞれの死亡の患者が抽出された時に、スコアが生存と死亡を適切に識別できる確率をそれぞれ平均すると0.88となります。これはROC曲線を描いた時のAUCと一致していることがわかります。このようにAUCとC統計量は算出方法は異なりますが、理論上同じものを指しています。
AUC(C統計量)の弱点
上の図で、C統計量とAUCを解説しました。これらの値を予測モデルの性能評価に用いる時の問題点は、「患者の順番」とアウトカムのイベント有無の分布を表しているだけで、どれくらい正確に予測できているのかという性能について評価できないという点です。
*予測モデルについては過去の記事を参照ください。
例えば、同じAUC(C統計量)= 0.94であっても、正確に予測できている場合とできていない場合があります。
例えば、以前の研究で、スコアが5点の場合は死亡確率が10%、8点の場合は死亡確率20%と予測できるとわかっていたとします。しかし下の図でみると5点から10点の人の10人中9人が死亡していることがわかります。スコアの予測によると、これらの患者の予測死亡は10-20% のはずで、このスコアでの予測はかなり過小評価していることがわかります。

このように予測性能は正確に予測できているか(較正能)が重要です。仮にAUC=0.94と非常に高い識別性能を持っていたとしても、予測が全く当たっていないということもあるので、予測性能を評価するときは較正能を評価することが重要です。
この辺りのところは下記の記事も参考にしてください。
以前の記事:臨床における良い予測モデルとはhttps://note.com/yohei_okada/n/nb62be74c093e
まとめ
この記事では模擬データを用いて、ROC曲線のAUCを実際に書いてみて、またC統計量を計算してみて、これらの意味するところをイメージできるように解説しました。C統計量もAUCも、検査値などの予測因子に基づいて患者を一列に並べ、その順番によってアウトカムのイベント発生の有無が識別できるかどうかを表しています。しかしこの識別性能だけでは、予測モデルの性能評価には不十分で、較正能も一緒に評価することが重要です。
この記事がROC曲線のAUC、C統計量の理解に役立てば幸いです。
