
ライツアウトの簡単な解き方の紹介
本記事の目的
本記事の目的は、ライツアウトというゲームに関して、プログラムなどに頼らず自分で実行できる簡単な解き方を説明することです。
$${n×n}$$ライツアウトとは、次のようなルールのゲームです。(本記事では$${n}$$は$${3}$$か$${4}$$か$${5}$$のいずれかだと思ってください。)
$${n×n}$$のマス目が与えられ、各マス目が点灯、または消灯のどちらかの状態である。
プレイヤーがマス目を選択すると、そのマスとそのマスの上下左右のマスの状態が反転(点灯↔消灯)する。
プレイヤーはマス目を選択していき、全てのマスが点灯している状態を作ることができたらクリア。
ライツアウトの解法については、知ってる人は普通に知ってると思いますので、本記事の内容自体は二番煎じならぬ百番煎じくらいでしょう。
しかし、「ライツアウト 解き方」等でググると「プログラミングで解いてみた」系の記事か「線形代数を使って理論的に解説してみた」系の記事に行き着いてしまい、具体的に自力で解く手順をストレートに教えてくれるページには少したどり着きにくいのではないでしょうか。
そこで本記事では、$${3\times 3}$$、$${4\times 4}$$、$${5\times 5}$$の場合にライツアウトを解く簡単な手順を分かりやすく説明したいと思います。(他の大きさのライツアウトも本質的に同じ解き方で解けます。)
なお本記事は、ブラウザの別窓などでライツアウトを実際にプレイして実験しながら読むことを推奨します。
(ライツアウトで検索すると、無料でライツアウトをプレイさせていただけるサイトがたくさんあります。私は特に、以下の二つのサイト様に大変お世話になりました。:
・bubudoufu様が公開されているサイト:ライツアウト (bubudoufu.com)
・よかひよかとき様が公開されているサイト:点灯パズル自動解答(ライツアウト) (yokatoki.sakura.ne.jp)
制作者のお二人に感謝申し上げます。もしも本記事からのリンクがご不快でしたら、クロイシヨウ(@Yoh_Kuroishi)/ X (twitter.com))までご連絡ください。
ライツアウトの解き方
解き方を説明するために、今から「下げアルゴリズム」というものを用意します。
まず「消灯マスの一つ下のマスを選択していけば、必ず消灯マスを一番下の行に集めることができる」という事実に注目してください。(つまり、消灯マスの一つ下のマスを選択していくことで、一番下の行以外は全て点灯させることができる、ということです。)
どういうことか、具体的な例で見てみましょう。
例えば$${5\times 5}$$ライツアウトの場合に、次の初期状態からスタートしたとしましょう。

試しに、上から一行目にある二つの消灯マスについて、それらの一つ下のマスを選択していってみましょう。(つまり、次の図2の左の画像から赤い✗印で示したマスを選択していくということです。)

すると図2の一番右の画像のようになり、一行目から消灯マスを消すことができました。
考えてみれば、選択したマス目を中心とする十字形にマス目の点灯・消灯が反転するので、消灯マスの一つ下のマスを選択していけば、消灯マスの位置を下げていくことができるのは当然ですね。
なお、右の赤い✗印のマスを先に選択して、その後に左の赤い✗印のマスを選択しても同じ結果(図2の一番右の状態)が得られることに注意してください。つまり、マスを選択する順番は関係ないということです。
この「点灯していないマスの一つ下のマスを選択する」という操作を続けていけば、いずれ一番下の行だけに消灯マスがある状態を作ることができますね。この記事では、この「上から順番に消灯マスの一つ下を選択していき一番下の行に消灯マスを集めること」を下げアルゴリズムと呼ぶことにします。
本記事で紹介するライツアウトの解き方は、基本的に次の3ステップからなります。
ステップ1: 下げアルゴリズムを適用する。
ステップ2: 適切なマスを選択する。
ステップ3:再び下げアルゴリズムを適用する。
但し、ステップ2で選択するマスは、ステップ1を適用した結果を見て決める必要があるため、全てのパターンを記憶する必要があります。以下では$${3\times 3}$$、$${4\times 4}$$、$${5\times 5}$$をクリアするのに必要なパターンを全て列挙しました。十分記憶できる量ですので、頭に叩き込んでください。
4×4 ライツアウトの場合
全てのパターンを記憶する必要がありますと言いましたが、実は$${4\times 4}$$の場合は記憶することはありません。
というのも$${4\times 4}$$の場合は下げアルゴリズムを適用するだけで自動的に解けてしまいます。説明するよりも実際に$${4\times 4}$$ライツアウトで下げアルゴリズムを適用してもらった方が早いと思います。やってみてください。
3×3ライツアウトの解法
ステップ1で書いたように、まずは機械的に下げアルゴリズムを適用してください。すると、次の図3の7つの状態のいずれかに行き着くか、または勝手にライツアウトが解けてしまいます。勝手に解けてしまう場合はそれでO.K.なので、図3の7つの状態に注目していきましょう。(この時点では、図の中の赤い✗印は無視してください。)
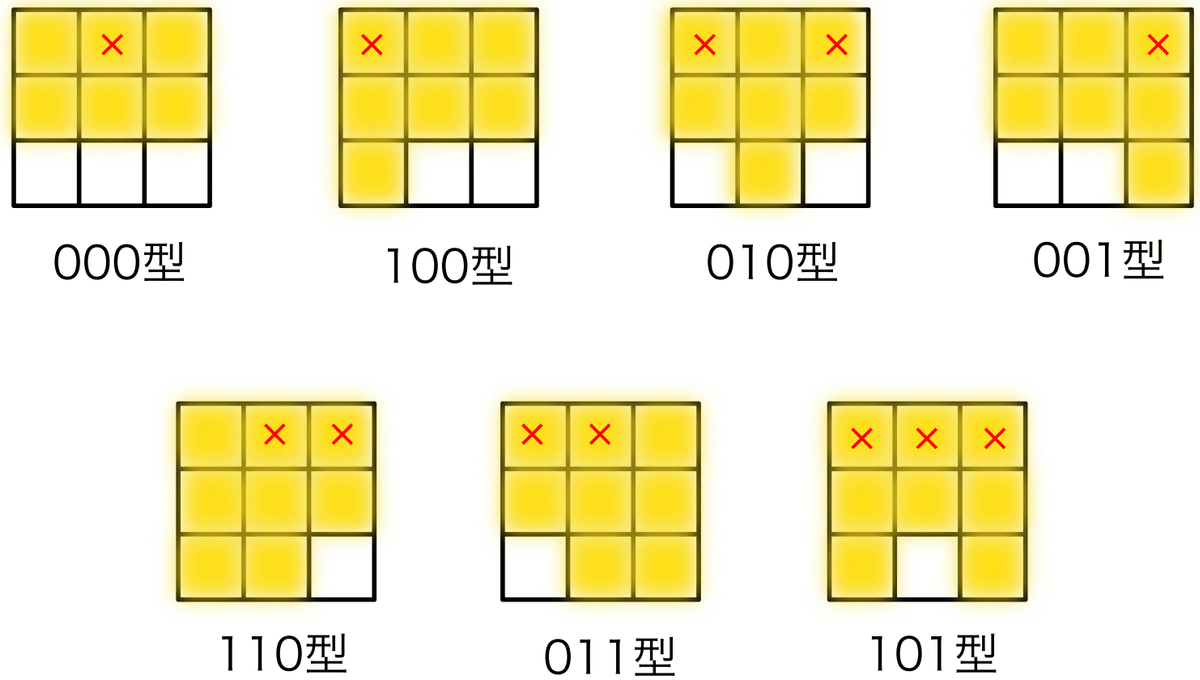
それぞれのライツアウトの状態に、000型、100型など名前が付いていますが、これは単に消灯マス=0、点灯マス=1と思って一番下の行を左から読んでいるだけです。
ステップ2では、ステップ1の後に現れた状態に応じて、図3の赤い✗印が描かれているマスを選択してください。(例えば、ステップ1の後で100型の状態が現れたなら、図3の100型で赤い✗印が描かれている一番左上のマスを選択する、ということです。)
ステップ3で下げアルゴリズムを再び適用したら解けます。
覚える必要があるのは、ステップ2においてどのパターンで、どのマスを選択するかということです。
少し覚えるのが大変そうに思えるかもしれませんが、100型と001型、110型と011型は左右を反転させると同じ状態になります。これらは選択するマスの位置も反転させればいいだけなので、覚えるべきパターンは実質5パターンのみです。
5×5 ライツアウトの解法
ステップ1として下げアルゴリズムを適用してください。すると、$${3\times 3}$$の場合と同様に、次の図3の7つの状態のいずれかに行き着くか、または勝手にライツアウトが解けてしまいます。

ステップ2では、$${3\times 3}$$の場合と同様に、ステップ1の後に現れた状態に応じて図4の赤い✗印が描かれているマスを選択してください。
ステップ3で、下げアルゴリズムを適用するとやはり$${3\times 3}$$の場合と同様に解けます。
$${3\times 3}$$の場合と同様に、左右を反転させれば一致する状態がありますので、$${5\times 5}$$の場合についても覚えるべきパターンは実質5パターンのみです。
数学的な背景について
(※ 以下の数学的な背景については、紹介だけして次の記事で解説を行なうつもりですので、ピンとこない人は「ふ〜ん、そういう話があるんだ」と思っていただけたらO.K.です。)
ご存知の方も多いと思いますが、実はこのライツアウトというゲームの背後には、線形代数という大学1,2年生の授業で扱われる数学が隠れています。
$${n\times n}$$ライツアウトを解く(全てのマスを点灯させるように、適切なマスを選択する)ことは、ライツアウトから定まるある連立方程式の$${\mathbb Z/2\mathbb Z}$$上での解を見つけることに対応しています。
そして、この連立方程式に解がいくつあるのかは、その係数行列の核の次元から簡単に計算できます。つまり、$${n\times n}$$ライツアウトが何通りの解を持つかが分かったりします。
数学的なことについては、次の記事(執筆中)でもっと詳しく述べたいと思いますので、しばらくお待ち下さい。
更新:
2023年12月31日: 情報が古くなっていたので「この記事を書くに至った経緯」の項目を削除しました。「追記」の項目についても完全な蛇足だったので削除しました。
