Inventor / ダイナミックシミュレーション / 構想設計で活用 (3)

引き続き、構想設計の時にダイナミックシミュレーションの機能を活用する方法を説明します。

旋回装置の構想設計での活用

1. アセンブリ構成

図のアセンブリモデルで説明します。どちらも、Z軸周りに旋回しますが、片方は重心を通る軸（重心軸）を中心に回転（旋回）します。もう片方は、重心と離れた軸（偏芯軸）を中心に回転します。

偏芯軸周りの方がバランス悪く、回転トルクもより必要だと、直感的にわかります。が、具体的に違いを数値で出そうとすると計算が大変です。ダイナミックシミュレーションを使えば簡単にできます。

標準ジョイントの回転に変換される

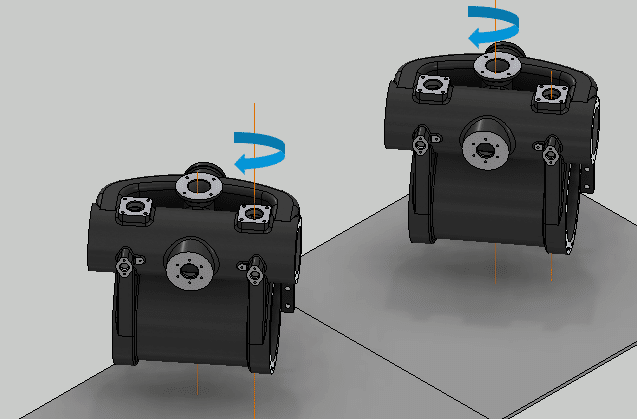
2. 等速回転

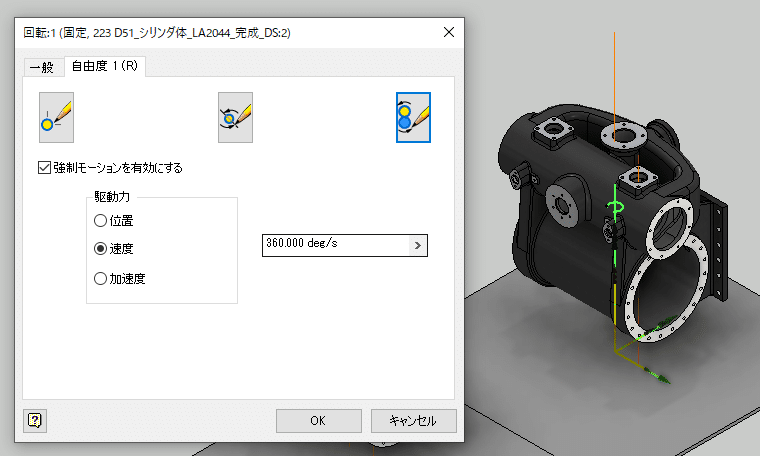
両方のジョイントの設定で、強制モーションを有効にして、速度を毎秒1回転(360 deg/s) とします。

223 D51_DS 03 Turn 03 等速回転.iam

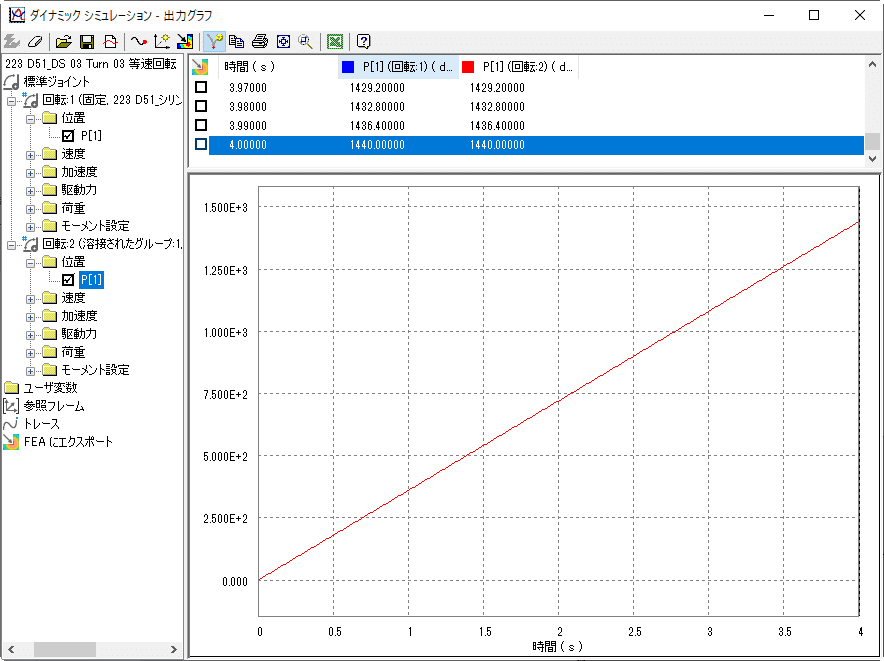
シミュレーションを実行すると、両方のコンポーネントは同じ動きをします。実際に出力グラフの結果も同じとなります。

4秒間で1440°（4回転）

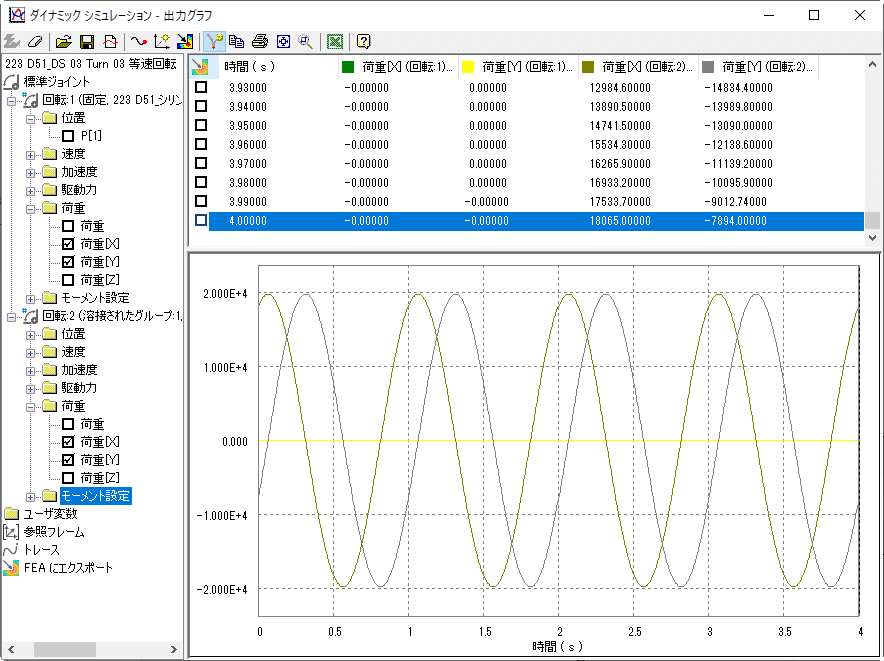
ところが、荷重のXY成分を見ると、重心軸周りの方はほとんど０なのに対し、偏芯軸周りの方は、XY方向に揺れていることが分かります。（数表の方を注目してください）

偏芯軸回転の方は、軸を揺らしている

2. 等トルク回転

両方のジョイントの設定で、ジョイントトルクを有効にして、トルクを1000 (N m) とします。

223 D51_DS 03 Turn 04 等トルク.iam

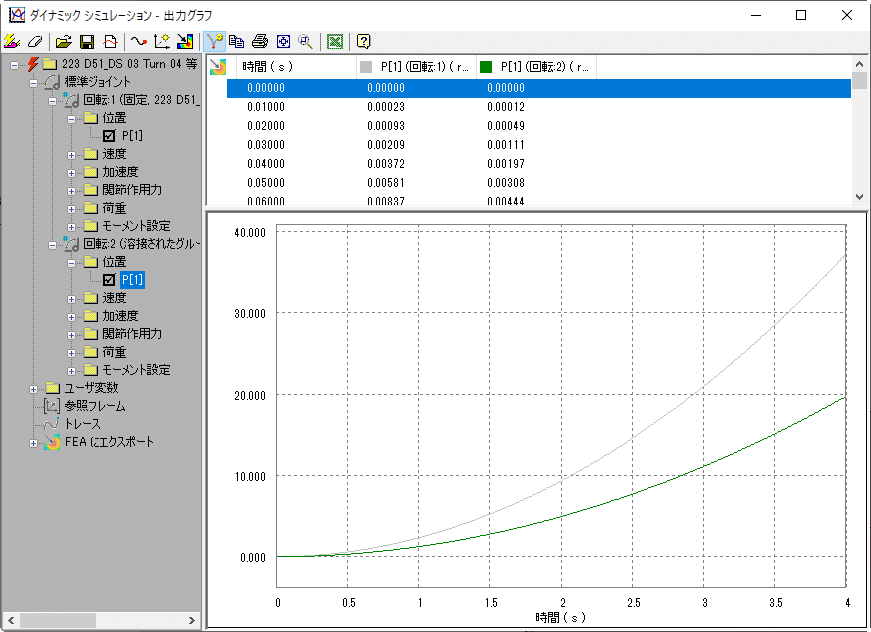
シミュレーションを実行すると、重心軸周りの方が早く回転することが分かります。回転軸周りの慣性モーメントが小さいからです。出力グラフで、4秒後の回転角度を見ると、大きく違うことが分かります。

回転角度の違い

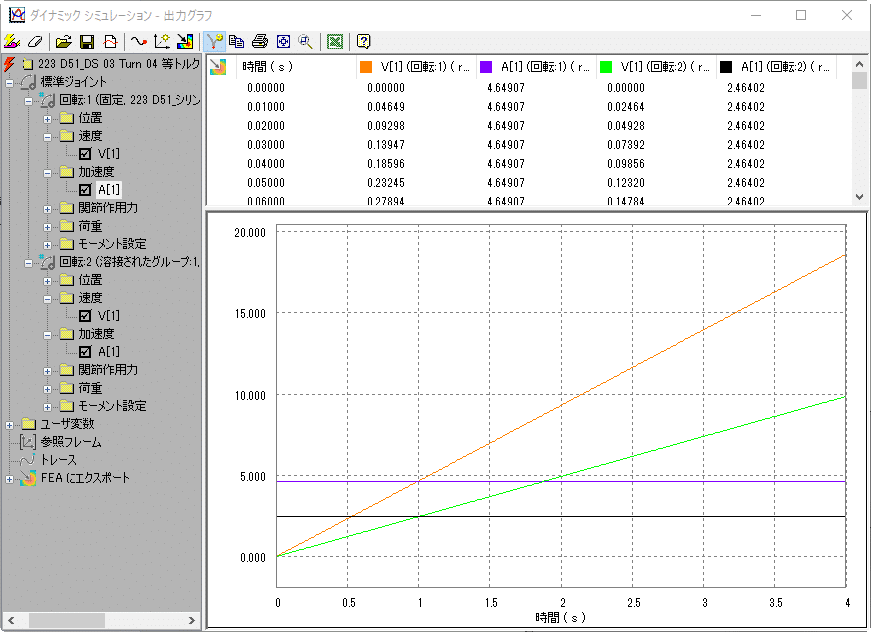
同様に、角速度、角加速度のグラフは以下のようになります。

角速度、角加速度

この様に、ダイナミックシミュレーションにおいては、ジョイントのプロパティの設定が正しく出来れば、速度、加速度、駆動力などの値をシミュレーションで簡単に求めることが出来ます。

3. 軸周りの慣性モーメントとトルク・角速度の関係

ダイナミックシミュレーションの一番良いところは、軸周りの慣性モーメントの計算をしなくても良い事です。

ただ、本当に計算が合っているかどうか、手計算で求めた慣性モーメントとシミュレーションの結果を検算してみましょう。

単位
軸周りの慣性モーメント I ： kg m^2
トルク T ：N m
角加速度 α :  rad/sec^2

T = I・α　（トルクは慣性モーメントと角加速度の積）
ここで、
I  : 軸周りの慣性モーメント： kg m^2
T : トルク ：N m
α : 角加速度 :  rad/sec^2

ニュートンの運動の第2法則

軸周りの慣性モーメントは、パーツモデルのプロパティから取得できます。エンジンブロックのパーツモデルをプロパティ→物理情報

慣性プロパティ

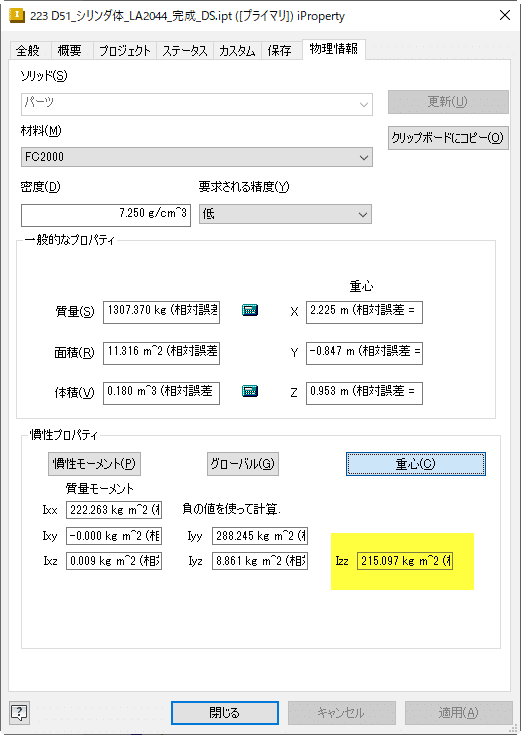
重心を通るZ軸周りの慣性モーメントは表から、215.097 Kgm^2 トルクは、
角加速度は、出力グラフの結果から、4.64907 rad/sec^2

※ 角加速度の角度がラジアンで表示されるよう、予めこのドキュメントの角度単位をラジアンにしておきます。

慣性モーメントと角加速度の積 = 215.097 x 4.64907 = 1000.001

となって、ジョイントプロパティの設定の 1000 N m と同じ値になるのが分かります。

データセット

等速回転と等トルク回転のアセンブリモデルはこちらからダウンロードできます。ダイナミックシミュレーションの設定済みです。