第21話 バックプロパゲーションの理解に必要な知識 -訓練データとテストデータ、損失関数-

今回からNN(ニューラルネットワーク)の学習アルゴリズムであるバックプロパゲーションの中身について学習していきます。
バックプロパゲーションを理解するためには次の5つの要素を知る必要がありました。

<バックプロパゲーションの理解に必要な5要素>
1　訓練データとテストデータ
2　損失関数
3　勾配降下法
4　最適化アルゴリズム
5　バッチサイズ

今回はこのうちの1と2について勉強していきます。
具体的な内容は次のとおりです。
・訓練データとテストデータ
・損失関数(二乗和誤差、交差エントロピー誤差)

それでは学習をはじめましょう。
(教科書「はじめてのディープラーニング」我妻幸長著)

訓練データとテストデータ

NNを学習させるためには多数のデータが必要になります。
この学習に必要なデータのことを訓練データといい、訓練データによって学習したNNがうまく学習できているかを検証するためのデータをテストデータといいます。
このようにNNの学習には2種類のデータを用意する必要があります。

訓練データの使われ方のイメージを示します。
訓練用の入力と正解のデータを使ってNNを学習させます。

学習が完了したら、学習させたNNが未知のデータに対して有効かどうかを、テストデータを使用して検証します。
テストデータの入力をNNに入れると、NNはなにかしらの出力を返してきます。
その出力と正解の誤差が小さければ、良い学習ができているということになります。(言うまでもなく出力＝正解がベスト)

出力と正解のイメージはこんな感じです。
分類問題のときは正解はどれか一つになるので、正解の配列は1が一つだけある形となります。これをone-hot表現といいます。

回帰・分類どちらの場合でも、出力と正解の誤差がどんどん小さくなればNNの学習が進んでいると言うことができます。

損失関数 -二乗和誤差と交差エントロピー誤差-

出力と正解の誤差を定義する関数です。誤差関数、コスト関数ともいいます。
今更ですが、誤差とはあるべき状態との解離の度合いのことです。
誤差が大きいとは、望ましい状態から離れていることを意味します。
NNの学習はこの誤差を最小化するように行われます。

損失関数にはさまざまな種類があるのですが、ディープラーニングでは二乗和誤差、交差エントロピー誤差を使用するのが一般的のようです。

二乗和誤差
出力値と正解値の差を二乗し、すべての出力層のニューロンで総和をとったものを二乗和誤差と呼びます。
数式で表すとこのようになります。

1/2は微分したときに便利だから付いています。(微分すると×2されて打ち消される。)
これを用いることにより、ニューラルネットワークの出力と正解の誤差を定量化することができます。

二乗和誤差は正解や出力が連続的な値のケースに向いているため回帰問題でよく使用されるようです。
Numpyのsum関数、square関数(引数を2乗する関数)を使って簡単に実装することができます。

交差エントロピー誤差
2つの分布の間のズレを表す尺度です。分類問題でよく使用されるようです。
次のような数式で表されます。

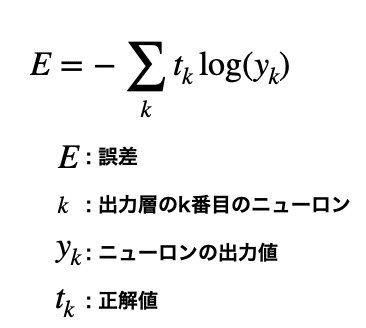
Σとlogが出てきて、一見よくわからない関数ですね。
ですが実はそんなに難しくありません。

先ほどのおさらいですが、分類問題では正解値はone-hot表現でした。
なので上式の右辺は、実は1項しか残りません。
先ほどの例だとはこのようになります。

こうなればあとは-logがどのような関数かを理解するだけですね。
ずばりこのような関数です。

xが1から遠ざかるほどyは大きく、xが1に近づくほどyは0に近づきます。
先ほどの例に当てはめると、y_3が正解の1から遠いうちは誤差Eは大きく、y_3が1に近づけば誤差Eは小さくなります。

交差エントロピー誤差は、出力値と正解値の解離が大きいほど誤差が大きくなる(0に近くなるほど無限に向かって増大)ので、学習速度が速く、出力値と正解値の解離が素早く解消できる利点があります。
Numpyのsum関数、log関数を使って実装してみましょう。

簡単に書けました。logの()内に1e-7とあるのは、log(0)とすると計算が止まってしまうためのを防ぐためです。(log0は無限に発散するので計算できない。)

一つ例をやってみます。
出力y1 = (0.18, 0.8, 0.02)と適当に定めて、正解をt1として、y1との解離によって誤差Eがどのように変化するか確認します。

y1とt1との解離が最も大きい一番右のコードで、誤差が最大になることがちゃんと確認できました。

まとめに入ります。
今回は、訓練データとテストデータ、損失関数(二乗和誤差、交差エントロピー誤差)について学習しました。
損失関数を理解したことにより、バックプロパゲーションにおける最初のステップである「出力と正解の誤差を算出する。」ことができるようになりましたね。

次回は勾配降下法について学習します。
それではまた(^_^)ノシ