遺伝的アルゴリズムでJR常磐線快速の停車駅を考える
この記事は東大航空宇宙2023 Advent Calendar 2022の9日目の記事です。2023年4月進学予定者の現B2の学生が面白い記事を書いてますので、他の記事も是非読んでみてください。
さて、私たちB2の学生は2022年の後期からは学科の授業を受けていますが、それ以前は教養学部の授業を受けます。私が前期で受講した講義のなかに、社会システム(投票論とか最適化法とか)を幅広く学ぶ講義があり、最終的にAIの仕組みなんかも簡単に勉強しました。そこで、せっかくなら話を聞くだけではなく実際に自分で遊んでみようと考え、趣味の鉄道と絡ませた結果、タイトルのように常磐快速線の停車駅最適化をしてみようとなりました。
おことわり
「最適化」系は大体そうだろうと思いますが、このような計算には現実のモデル化が含まれ、結果にはモデル化による誤差が影響します。特にこの記事では、現実を非常に簡単なモデルで無理やりモデル化しているため、このモデル化誤差が大きいことが想定されます。
そもそも遺伝的アルゴリズムを用いているので、結果が大域的最適解である保証はありません。
イメージしやすくする目的で現実の路線や駅をそのまま利用していますが、あくまで妄想として現実とは切り離して考えてください。
JR常磐線(上野~取手間)について
JR常磐線は、東京都の日暮里駅から宮城県の岩沼駅までを結ぶ路線です。運転系統としては、上野駅(上野東京ライン経由の品川発もあり)と仙台駅の間で運転されています。この記事で着目するのは、そんな中でも上野駅と取手駅の間の区間(図1に駅一覧を示す)です。この区間は首都圏の通勤需要を担っており、柏や松戸などの一大ベッドタウンを貫くため需要も大きい区間です。この内、北千住~取手間(注1)は複々線(線路4本)を構成しており、途中一部の駅にしか停車しない快速電車、普通列車及び特急列車が走行する急行線と、各駅に停車する各駅停車が走行する緩行線に分かれています。以下では、この急行線を走行する列車群を「快速」と、緩行線を走行する列車群を「各駅停車」と一本化して呼称します。特急については今回は考えません。
常磐線快速の特徴としては、やはりスピードが挙げられます。松戸~柏間の駅間11.2kmに象徴される駅間の長さに加え、最高130km/h運転(快速は上野~取手間では120km/hぐらい)により、都心と郊外とを高速で結びます。東京→茨城方面は、常磐線快速・つくばエクスプレス線と高速路線が多く、距離の割に時間はかからないなという印象です。
快速運転のメリットは時間短縮にとどまらず、近距離の乗客と遠距離の乗客を各駅停車と快速電車に分けて、混雑を分散させるというメリットもあります。話がそれますが、西武池袋線はこのような観点で見ると面白く、快速急行も停車する石神井公園を通勤準急が通過したり、停車駅の多い通勤急行が快速急行の停まるひばりヶ丘を通過したり、と混雑の分散を目的に停車駅をバラけさせているように思います。
快速など優等種別の停車駅決定は、所要時間短縮、混雑分散などの観点から総合的に判断して決定されていると推察しますが、この問題を、所要時間や混雑の偏りを表現する評価関数を最適化する問題に落とし込んで、遺伝的アルゴリズムを適用してみます。
注1 :正確には、北千住~綾瀬間は東京メトロ所有の千代田線となり、常磐線各駅停車は綾瀬~取手間です。しかし後述するように、この記事では複々線が上野駅まで続くとしてしまうので、影響しません。
遺伝的アルゴリズムとは
課題が多くてこの章を書く余裕が無いので、わかりやすい解説サイト様へ丸投げさせていただきます。
今回は、二点交叉、突然変異あり、ルーレット選択方式、エリート保存なしで実験しました。遺伝子は、各駅で優等列車の通過/停車の2通りに、始発駅における快速と各駅停車の発車時刻の差(0~10分)を0.5分単位で表現するため、$${\mathrm{(駅数)}-2 + 2 \times 5=\mathrm{(駅数)}+8}$$bitの長さを持ちます。始発着駅は必ず停車ですから$${-2}$$、20通りの時間差を上下で示すために$${2\times 5}$$bitです。
問題設定
評価関数
「最適化」を数値的に扱うには、現実をモデル化し、人間が思う「最適」を表現できるような評価関数を設計する必要があります。今回の例では、停車駅、ダイヤをパラメータとして、移動にかかる時間、混雑の偏りなどを返す関数を評価関数として設定してやればよさそうです。ここでは、評価関数の設定について考えます。
まずは評価関数の全体を見てみます。今回、最適化する評価関数は次のように設定しました。
$$
f=\sum_{i\neq j}N_{i,j}t_{i,j}+A \sum_{i} \left(\frac{r_{i,i+1}-l_{i,i+1}}{r_{i,i+1}+l_{i,i+1}}\right)^2
$$
ただし、$${N_{i,j}}$$は$${i}$$駅から$${j}$$駅へ向かう人数、$${t_{i,j}}$$は$${i}$$駅から$${j}$$駅へ向かうのにかかる最短の時間、$${r_{i,i+1}}$$と$${l_{i,i+1}}$$はそれぞれ、$${i}$$駅~$${i+1}$$駅の間を快速電車で移動する人数の合計、各駅停車で移動する人数の合計です。したがって、第一項は移動時間に移動人数の影響を入れたものであり、これを小さくすればするほど、多くの人にとっての時間短縮になると考えられます。また、第二項は快速の乗客数と各駅停車の乗客数が完全に等しいときに0となり、どちらかに偏るほど1に近づきます。そのため、第二項は混雑の偏りを表すと言えます。しかしそのままでは数値の大きさが違いすぎるため、係数$${A}$$を掛けて、混雑の偏りをどの程度考慮するかを調整します。($${A=0}$$とすれば、純粋に移動時間のみを考慮した最適化になります)
移動人数
評価関数の計算には、ある駅からある駅へ向かう旅客の数が必要ですが、この情報はおそらく入手できません。そこで今回は単純化して、駅の乗車人数から推定することにしました。ここは結構適当で、A駅からB駅への移動人数は、A駅の乗車人数に、A駅以外の駅の乗車人数の総和に対するB駅の乗車人数の比を乗じたものとしました。式で書くと、$${i}$$駅の乗車人員を$${N_i}$$と書くことにすれば、
$$
N_{i,j}=N_i \times \frac{N_j}{\sum_{k \neq i} N_k}
$$
となります。
駅の乗車人数は、JR東日本の各駅の乗車人員の2021年度のデータを用います(執筆時最新データ)。
移動時間
快速運転により所要時間は短縮されますが、モデル化のためには停車駅の情報から所要時間を推定する必要があります。今回は、すべての駅に停車する場合の所要時間(現実の各駅停車のデータが使える)をベースとして、通過駅数ごとに所要時間が一定の分数だけ短くなるとして考えます。実際のデータで通過駅数と短縮時間をグラフにしてみると、一駅ごとに1.5分づつ短縮されると考えればよさそうです。(図2)

そして、旅客は常に最速かつ乗り換えの最も少ない経路で移動するとします。乗り換えが必要なら乗り換えますが、乗り換えても所要時間が変わらない場合は乗り換えません。
その他の仮定
モデルを簡単にするため、次のような仮定をおいています
通過待ちはない
複々線であるため、任意の地点で各駅停車の追い抜きが可能であるため
複々線が上野まで続く
結構重要かつ現実と一番異なる仮定です。常磐線各駅停車は北千住(正確には綾瀬)から千代田線に直通し、北千住から日暮里間は複線となり、快速電車も同区間では各駅に停車します。しかしながら、直通運転まで考えると複雑になりそうだったので、勝手ながら今回は上野駅まで複々線が続き、各駅停車と快速電車が始発から終点駅まで通しで運転されるとしました。
運転は10分間隔
日中パターンダイヤは現実でもおおよそ10分間隔です(区間によって異なる)。この仮定を置けば、各駅の時刻を1の位だけ考えれば良くなります。(3, 13, 23分のように来るなら、3だけ考えれば良い)
乗り換えは最小0分で可能
対面乗り換えを想定しています。A駅で各停が「3」に発車、快速が「4」に発車であれば各停から快速は1分で、「4」, 「4」であれば0分、「5」, 「4」なら9分です。
結果と考察
pythonで実装して学習させてみます。それぞれ一世代あたり100個体、200世代くらいまで学習させることを何回かやって収束させています。突然変異率は1%としました。
快速を運転しない場合の総所要時間は、16578855(人・分)でした。以下では、快速運転時の時間をこの時間と比較し、快速運転の効率を示す尺度として用います。
純粋な所要時間短縮
$${A=0}$$の場合に相当します。この場合の列車ダイヤグラムを図3に示します。

グラフは横軸の数字が時刻(分単位)を表していて、左から右へ行くほど時間が経過していきます。列車の各駅での発車時刻を線で結ぶと一本の線になり、この線を見ることで時刻による位置がわかります。青は各駅停車を表していて、オレンジは快速電車を表します。
上り列車について見てみると、松戸駅を堺に、青線の右側にあったオレンジ線が青線の左側へ来ていますが、これは松戸駅で快速電車が各駅停車を追い抜いたことを表します。正確な出力を見ると、松戸駅の発車時刻は揃えられていて、(差は0分ですが今回のモデルでは)乗り換えが可能です。すなわち松戸駅で緩急接続が行われます。この緩急接続により、北松戸~南柏と北千住や上野間との所要時間を短縮できています。現実の路線でも非常によく見られるダイヤです。
柏~取手で各駅に停まっていますが、利用者の多い柏には停めるとして、柏での接続があまり良くないのでその先も各駅に停めるということでしょうか。このような、〇〇から各駅停車になるという停車パターンも現実で見受けられます。
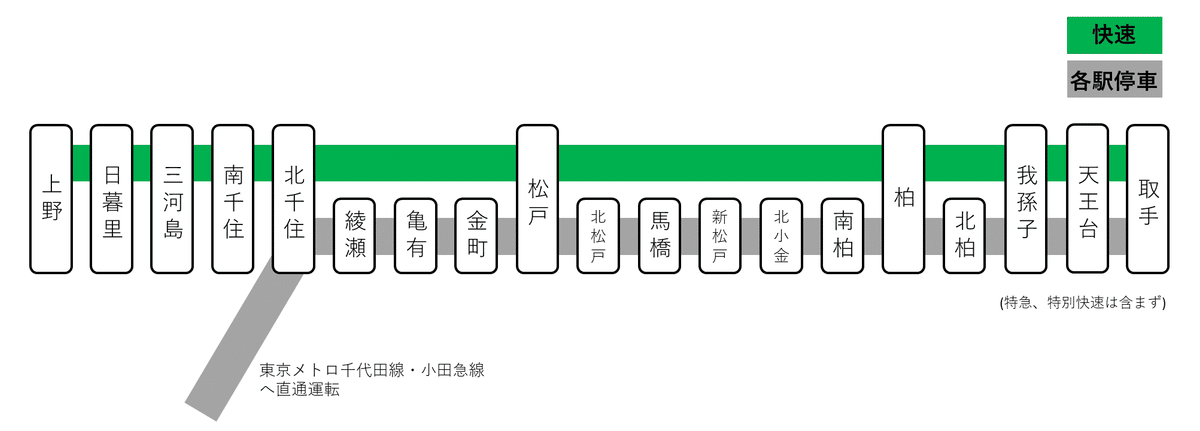
この停車パターンの場合、総所要時間は12110509(人・分)で約27%の時間短縮ができています。続いて、混雑の偏りを見るため、駅間通過人数を種別ごとに示した棒グラフを図4に示します。

このグラフからも、松戸を堺に各駅停車から快速と、その逆の乗り換えが行われていることが明らかです。快速の最混雑区間は松戸~北千住間で、この区間では乗車人員に4倍近い差ができるようです。この停車パターンでは、取手~松戸の全駅から北千住、日暮里、上野へ至る最速ルートが快速経由となるため、混雑は当然と言えば当然です。次節では、混雑の平準化も評価関数に取り入れて改善するか調べます。
現実で快速運転が行われている北千住~取手間を見ると、現実の停車駅との差は北柏のみです。実際は松戸で0分乗り換えなんてできませんし(ホームが異なるため)、乗り換えの案内もないので一概に比較はできませんが、現実のダイヤはモデルの最適解に近く、良く考えられているなと感じます。
混雑分散の考慮
$${A}$$の値を適当に設定してやってみます。とりあえず、$${A}$$には全く運転しない場合の所要時間16578855を入れてみました。学習の条件は同様です。
この場合のダイヤグラムを図5に示します。

続いて、駅間通過人数を図6に示します。
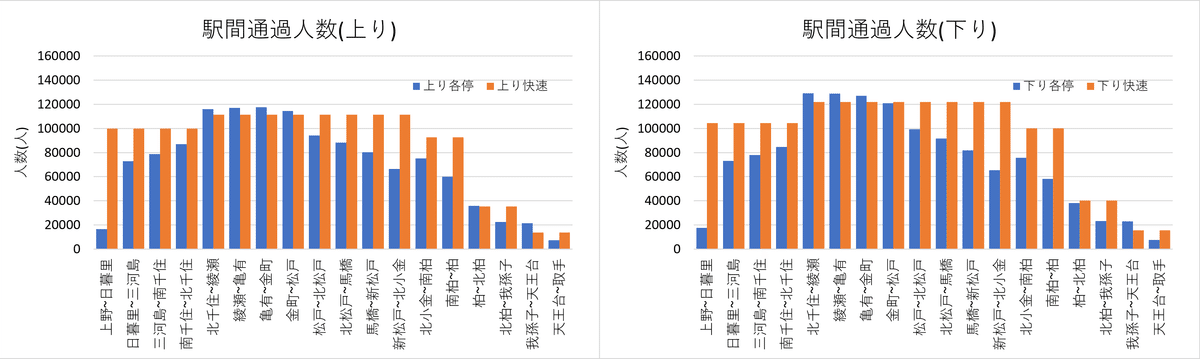
図の見方は同様です。図6からは混雑の偏りが大きく改善されていることが見て取れます。また、所要時間も12862834(人・分)と、約22%の短縮ができています。
まずはダイヤについて、緩急接続の観点から眺めてみます。上り下りは逆になるだけでほぼ同じですので、上りを中心に考えます。見たところ、北小金と北千住で乗り換えができそうですが、詳細な出力を見ると北小金では時刻が30秒差と微妙にずれています。そのため、乗り換えの方向が、上りでは各駅から快速、下りでは快速から各停に制限されます。おそらくこれは、松戸、新松戸、金町等と柏や我孫子、取手といった乗り降りの多い駅同士での移動において、旅客を各駅停車に誘導するためと思われます。北小金で各駅停車に追いつけないため、例えば柏から松戸に行くなら各駅停車に乗る必要があります。実際に発車時刻を揃えたところ、快速の乗車人員が大幅に増え、混雑の偏りの項が効いて評価関数の値が増加してしまいました。しかしながら、このような接続逃げは、利用者としてはあまり嬉しくありませんね。
一方の北千住では双方向の乗り換えが可能で、取手~北小金と北千住~上野間の移動では快速を間に挟むことで10分近く時間が短縮できます。各停には快速からの乗り換え客が入りますが、同時に松戸等からの大量の乗客が降りるため混雑に大きな差はできていません。
松戸の通過など、正直結果を見たときには少し驚きましたが、詳しく見ていくと、駅ごとにうまく使う列車を分けさせつつ、緩急接続によって快速と各駅停車がうまく連携できているように思います。
しかし、現実的な話として、利用者が非常に多い松戸を通過することはまずありえませんし、新宿方面へ直通する列車の運行がない常磐線において、日暮里の通過により、快速→山手線内回りという新宿方面への最速乗り継ぎができなくなるのは痛手かと思います。特に利用者の集中するラッシュ時限定とかなら、ギリギリありえなくもないかなという印象です。(もうなくなりましたが、東海道線通快の川崎・横浜通過と似たような例はあり)
比較
各駅停車のみを運転する場合と混雑分散を考慮しない場合、そして混雑分散を考慮する場合で、代表的な駅までの所要時間をグラフ化してみます。
図7に上野・北千住・松戸駅までの所要時間のグラフを示します。

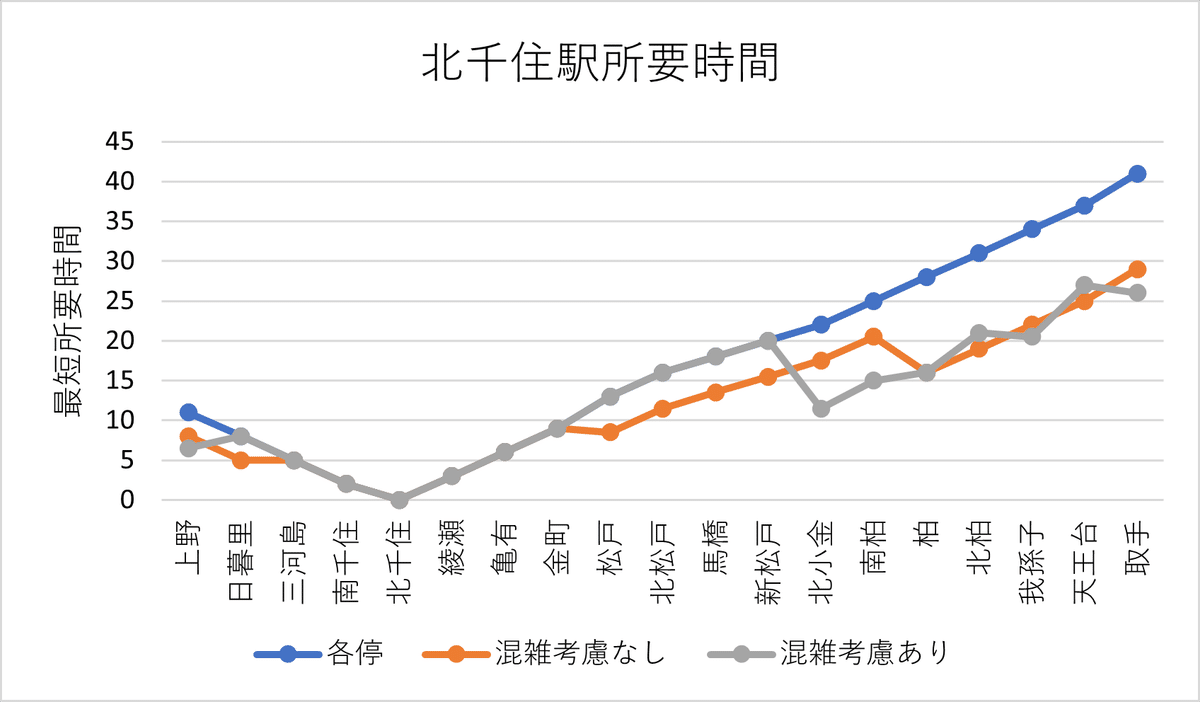

こうしてみると、上野と北千住までの所要時間に関しては、一部の駅を除いて混雑の偏りを考慮しない場合とする場合で大きな差はないように見えます。一方で、松戸駅までの所要時間では、混雑の偏りを考慮する場合には殆どの駅で快速が利用できないため、時短効果はほとんど現れていません。混雑分散を考慮した場合については、このグラフで見ても、松戸~北千住間の利用人数の多い駅同士の移動を、乗車人員が少なくなりやすい各駅停車に誘導しようという意図が感じられます。
まとめ
少々長くなりましたが、いかがだったでしょうか。アドベントカレンダーや記事を書くのは初めてなので読みづらい箇所もあったと思いますが、楽しんでいただけたなら幸いです。大部分がオタクの独り言状態ですが……
遺伝的アルゴリズムで停車駅決定をしてみましたが、混雑の偏りを考慮しない場合では現実にかなり近い結果を得られたり、緩急接続などを行っていたり、個人的には満足いく結果が得られたなと思っています。今回は10分間隔で運転としましたが、各駅5分間隔、快速10分間隔としてみたり、両者5分間隔にしてみたりすると、また結果が変わってくるような気がしています。また、直通運転の考慮も必要です。また、今回は複々線ということで通過待ちは考えませんでしたが、複線では優等列車の退避も考慮する必要があります。これができると、より一般の路線に本手法を適用できます。
この記事が気に入ったらサポートをしてみませんか?
