
Bybitの約定データ分析(正規性の検証)
やりたいこと
約定データが正規分布に従う前処理方法を探し出したい。
そこでタイムバーの幅を変えてみたり、ドルバーを導入したりして正規性の検定を行なった。
結論からすれば、なかなか直球では困難であった。
ポジティブに捉えれば約定データが完全なランダムではなく、どこかにαが隠れていると考えることもできる。また、失敗したケースも、バーの作成方法、検証方法などノウハウとして有用であろうことから公開する。
なお、最後にドルバーを作成し、かつ、例外値の2%を削除した98%で分布をつくると正規分布になる可能性が発見できた。ただし、その場合、例外の2%で激しく焼かれるということを意味している可能性もあり現段階では実用性があるかどうかは未知数である。
Google Colabで動かせるようにしてあるので是非いろいろ検証してコメントを寄せて欲しい。
ドルバーについては、UKIさんのnoteが参考になる。
検証したBybit 約定データ処理方法
1)イベントバー:生データ分布 T1, T2,,,,,Tn
2)タイムバー:収益の分布(前Tickとの差分) (T2-T1), (T3-T2),,,, (Tn-T(n-1))
3)タイムバー:収益率(前Tickとの比率)(T2/T1), (T3/T2),,,, (Tn/T(n-1))
Tickは生データは約定毎にレコードが生成されるので、ある意味イベントバーに該当するが基本±0.5ドルの値動きしかしないため役に立たない。その後タイムバー(分足、時間足)で確認した。
最後に「ファイナンス機械学習」の2章で提案されている正規性が高まる方法である、ドルバーについても確認する。
正規性の検証方法
「pythonによるファイナンス」(13.1章)の方法にしたがって検証する。
1) ヒストグラムのプロット distplot
2)QQプロット probplot
3) 統計的検定の実施 normaltest
検証方法の検証
まず検証がうまくいったケースを確認するため正規分布に従う乱数を発生させ、上記検証方法で正規分布として判定する。
具体的には、以下を検証する。
1) 分布がいわゆるベルカーブになっていること
2)QQプロットが直線になっていること
3)検定結果がすべて p > 0.05 であること
当然ながら正規分布に従う乱数を生成しているので上記条件はクリアする(はず)。
正規分布に従う1000個の乱数の正規性を確かめるコード
乱数の生成
# 正規分布にしたがう数値1000個の生成
import numpy as np
import scipy.stats as stats
random_norm = np.random.randn(1000)以下は数列をグラフ化し正規性の統計検定を行うコード。以後データ生成後は繰り返し同じパターンで使う。
# ヒストグラムの表示
import seaborn as sns
from matplotlib import pyplot as plt
print('見た目がベルカーブにしたがっていることを確認する。')
sns.histplot(random_norm, bins=100, kde=True)
plt.show()
# QQプロットの表示
print('赤い線との乖離が小さい方が正規分布にしたがっていることを示す')
stats.probplot(random_norm, plot=plt)
plt.show()
# 統計的検定の実施
print('以下の統計数値のpvalueがすべて0.05を下回っていないことを確認する')
print(stats.skewtest(random_norm))
print(stats.kurtosistest(random_norm))
print(stats.normaltest(random_norm))出力
綺麗なベルカーブになっている。
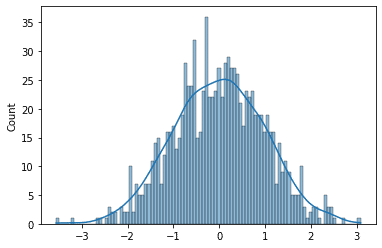
QQPlotは赤い線に近いと正規分布といえるがきちんと揃っている。
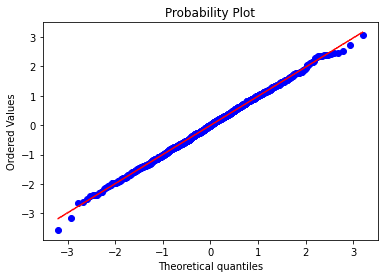
検定数値も以下のとおり合格。
SkewtestResult(statistic=-0.3436109868591484, pvalue=0.7311388609785899)
KurtosistestResult(statistic=-0.6040311640263974, pvalue=0.5458229230780871)
NormaltestResult(statistic=0.48292215740540256, pvalue=0.7854793750703232)このやり方で正規性の検定ができそうだ。
Bybitのデーターで検証
データダウンロード用の関数の準備
前回のNoteと同じものに、一括して過去N日分のデータを取得するget_bb_df_past_daysを追加した。
# bybitのデータを取得する関数の定義
def get_bb_log(yyyy, mm, dd, symbol="BTCUSD"):
"""
bybitからパラメーターに指定された日付の約定データを/tmpにダウンロードする。
/tmpに一時保存することでキャッシュ機能を実現
:param yyyy: 年(4桁)
:param mm: 月
:param dd: 日
:param symbol: オプション:ディフォルトBTCUSD
:return: /tmpにダウンロードしたファイル名
"""
file_name = f'{symbol}{yyyy:04d}-{mm:02d}-{dd:02d}.csv.gz'
tmp_file = '/tmp/'+ file_name
if not os.path.exists(tmp_file):
download_url = f'https://public.bybit.com/trading/{symbol}/{file_name}'
print("download url=", download_url)
request.urlretrieve(download_url, tmp_file)
return tmp_file
def get_bb_df(yyyy, mm, dd):
"""
bybitから約定データをダウンロードしpandasのDataFrameオブジェクトにする。
:param yyyy: 年(4桁)
:param mm: 月
:param dd: 日
:return: 約定データが入ったDataFrame
"""
file = get_bb_log(yyyy, mm, dd)
bb_df = pd.read_csv(file, index_col=0)
bb_df.index = pd.to_datetime(bb_df.index, utc=True, unit='s')
return bb_df
def resample_ohlcv(data, sample_time):
"""
約定データからohlcvを作成する。
timeに指定できるパラメータは文字列で以下のように指定する。
15秒:'15S' / 1分: '1T' / 1時間: '1H'
詳細はpadnasのドキュメント
https://pandas.pydata.org/pandas-docs/stable/user_guide/timeseries.html#offset-aliases
:param data: bybitの約定データの入ったDataFrame
:param sample_time: サンプル間隔
:return: ohlcvデータ
"""
resample_df = data['price'].resample(sample_time).ohlc()
resample_df['volume'] = data['size'].resample(sample_time).sum()
return resample_df
def get_bb_df_past_days(days=10, start_day = None):
"""
Bybitから過去から指定期間のデータをダウンロードしdfを返す。
データが生成できていない可能性があるので2日前までの期間のデータをダウンロードする。
:param days: データ取得期間
:param start_day: 開始時間(指定しない場合は今日からdays+2日前)
:return: 約定データが入ったdf
"""
if not start_day:
start_day = datetime.date.today() - datetime.timedelta(days=days+2)
print('start:', start_day, "-> end:", start_day + datetime.timedelta(days=days))
bb_df = None
for i in range(days):
target_day = start_day + datetime.timedelta(days=i)
download_df = get_bb_df(target_day.year, target_day.month, target_day.day)
if bb_df is None:
bb_df = download_df
else:
bb_df = bb_df.append(download_df)
return bb_df10日分の約定データ(生データ)での検証
get_bb_df_past_days関数をつかって10日分のデータをダウンロード&検証。まったくベルカーブにならず正規分布に形も似ていない。
df = get_bb_df_past_days(10)
price = df['price']
print('見た目がベルカーブにしたがっていることを確認する。')
sns.histplot(price, bins=100, kde=True)
plt.show()
# QQプロットの表示
print('直線にならんでいると正規分布にしたがっていることを示す')
stats.probplot(price, plot=plt)
plt.show()
# 統計的検定の実施
print('以下の統計数値のpvalueがすべて0.05を下回っていないことを確認する')
print(stats.skewtest(price))
print(stats.kurtosistest(price))
print(stats.normaltest(price))出力
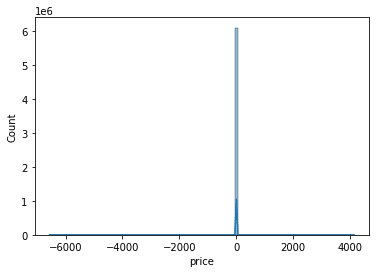
10日間に42500ドル、43500ドル、47500ドル付近の3つでヨコヨコのフェーズがあったようだ。まったくベルカーブになっていない。
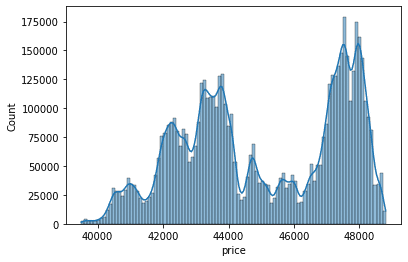
QQPlotも当然NG
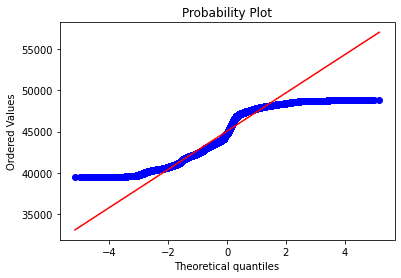
検定数値もすべて0.05以下で正規性は否定された。
以下の統計数値のpvalueがすべて0.05を下回っていないことを確認する
SkewtestResult(statistic=-131.05144853400958, pvalue=0.0)
KurtosistestResult(statistic=12595.213622343857, pvalue=0.0)
NormaltestResult(statistic=158656580.67463914, pvalue=0.0)約定毎の差分の検証
1つ前の約定との差分をとって検証。グラフ化するコードはこれまでと同じなので以後省略。
price_diff = price.diff()ByBitの場合0.5ドル刻みでしか価格は変動しないので、-0.5, 0, 0.5の変化に分布が集中しベルカーブにならない。
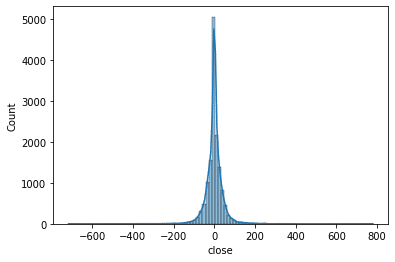
1分足を作成し1分間隔での差分の分布の検証
price = resample_ohlcv(df, '1T')['close']
price_diff = price.diff().dropna()1分では値動きが小さくとてもピーキーな分布になり正規分布とは異なる。次は一時間足で試す。
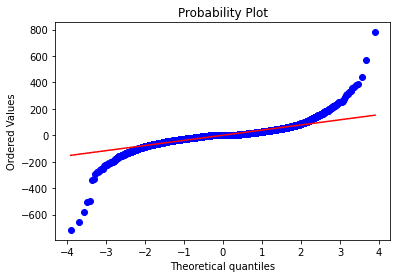
一時間足での差分検証
一時間足の作成部分のコード。
price = resample_ohlcv(df, '60T')['close']
price_diff = price.diff().dropna()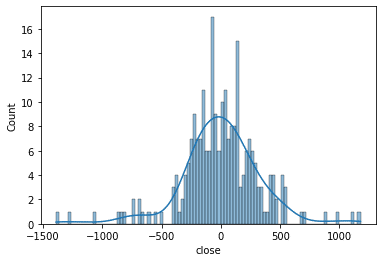
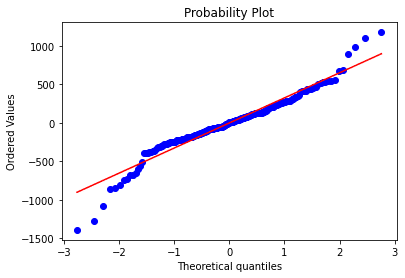
かなりいい線まできたようにみえるが統計検定では以下の通りNG
SkewtestResult(statistic=-2.1205822729647656, pvalue=0.03395697122501914)
KurtosistestResult(statistic=4.697416376169, pvalue=2.6347299871930947e-06)
NormaltestResult(statistic=26.56258978751312, pvalue=1.7061095545433092e-06)一時間足の収益率(比率)での検証
price.shift(1)で 1レコード(1時間)先のデータとの比率をもとめる。
price = resample_ohlcv(df, '60T')['close']
price_ratio = (price.shift(1) / price).dropna()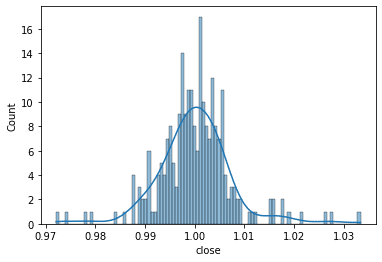
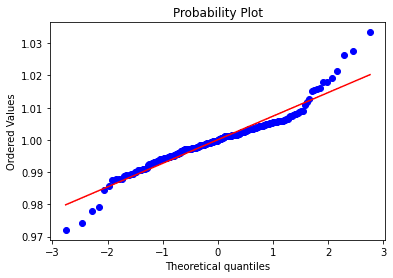
数値的にはむしろ差分よりも悪くなっていた。おそらくどちらがいいというレベルではなく、取引状態によって変化する誤差のレベル。
SkewtestResult(statistic=2.474763482331523, pvalue=0.013332443670861028)
KurtosistestResult(statistic=5.124779180198452, pvalue=2.9788665832361156e-07)
NormaltestResult(statistic=32.38781593927716, pvalue=9.269901689724221e-08)ドルバーでの検証
差分や比率のlogを取るなどいくつか試してみたが時間バーでは限界があるようだった。「ファイナンス機械学習」で紹介されている取引高毎にTickを刻むドルバーで検証する。
計算方法は以下:①取引高の累積を計算する。②単位取引高刻みのカラムを作る。③groupbyで累計取引高刻みのバー(ドルバー)にまとめる。④その後、一つ前の行との差分(diff)を取得する。
# 累積取引高のカラムを追加
df['cumsum'] = df['size'].cumsum()
# 累積取引高を50_000_000ドル刻みで dollar カラムとして追加する
df['dollar'] = round(df['cumsum']/50_000_000)
# 取引高刻み毎にグループ化い平均をバーの値とする。
dollar_returns = df.groupby('dollar')['size'].mean()
dollar_returns = dollar_returns.diff().dropna()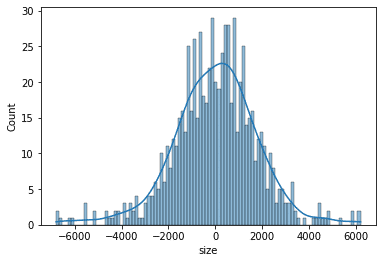
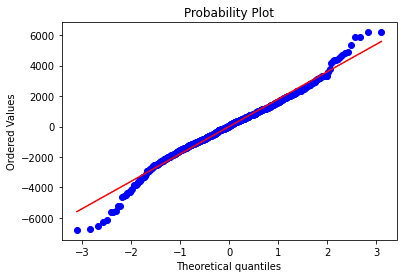
SkewtestResult(statistic=-2.5381748699772584, pvalue=0.011143228932166812)
KurtosistestResult(statistic=5.130693738170336, pvalue=2.886762679076347e-07)
NormaltestResult(statistic=32.766349905484375, pvalue=7.671451115877571e-08)統計数値的にはまったくNGである。しかし、QQPlotの形が両端の例外を除けばよくFITしているように見える。
そこで次は例外を除外して検証する。
ドルバーの例外を除外した場合の検証
99パーセンタイルの値を見つけ出す。
q = dollar_returns.quantile(0.99)
上下1%を切り取る
dollar_returns = dollar_returns[(dollar_returns < q) & (-q < dollar_returns)]いつものようにグラフで検証
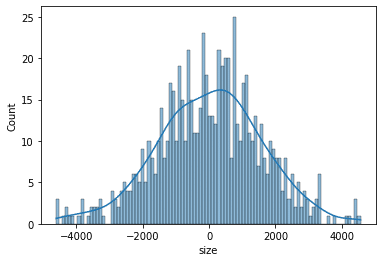
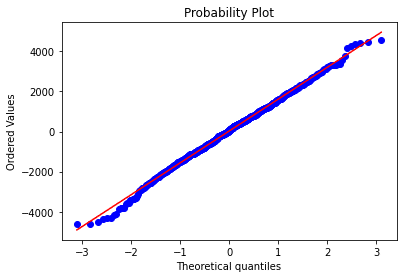
SkewtestResult(statistic=-1.1959114316574893, pvalue=0.23173112360344816)
KurtosistestResult(statistic=0.8245165290925731, pvalue=0.40964612787204246)
NormaltestResult(statistic=2.1100316591159296, pvalue=0.3481869156176107)これはもしかして、うまく正規分布に前処理できたということでいいのだろうか?
まとめ
上下1%の例外を切り出し98%のデータで確認することの意味が、焼かれるときは本格的に焼かれるということを意味している可能性があるが、ドルバーを使うことで正規分布にしたがう前処理が可能となった。
ソース全体
タイムバーやドルバーの幅など、いろいろ変化させて試してみたい方のために以下をクリックするとGoogle Colabですぐためせるようにしました。ぜひいろいろ試して結果を教えて欲しい。
ちょっと試した感じでは、ドルバーの幅を大きくするとlogや比率にするほうが良いFIT感がでるように見える。
