暗号理論（３）

はじめに

こんにちは、No.5です。
今回も暗号についての記事となります。

暗号理論１回目は公開鍵暗号とRSA暗号、
暗号理論２回目は秘密分散法を紹介しましたが、
暗号理論３回目のAll-Or-Nothing Transformという暗号化方式を紹介します。

---

All-Or-Nothing Transformとは

All-Or-Nothing Transform（以下、AONT方式）とは、暗号に対する様々な攻撃（総当たり攻撃、選択平文攻撃、関連平文攻撃、差分攻撃）に対する安全性を高めるための方式です。
Ronald L. Rivestが1997年に「All-Or-Nothing Encryption and The Package Transform」[1]という論文で発表しました。

秘密情報である平文を固定長のブロックに分割し、ブロックごとに変換処理を行った後に既存の暗号化処理を行います。
分割されたブロックを分散することで、暗号理論（２）で紹介した秘密分散法と同じ使い方をすることができますが、AONT方式ではブロックが１つでも足りないと復号することができないという特徴があります。
秘密分散法は秘密情報を𝑛個に分散したシェアを𝑘個集めると復元できる方式ですが、AONT方式は𝑛個すべて集めないと復元できないことから、(𝑛,𝑛)しきい値秘密分散法と呼ぶこともできます。

また、Shamirの(𝑘,𝑛)しきい値秘密分散法 [2]では、秘密情報を分散したシェアのデータサイズが秘密情報と同じになる仕組みのため、多数のシェアに分散するとシェアの合計サイズが非常に大きくなっていました。
それに対して、AONT方式はシェアの合計サイズが秘密情報とほとんど同じという特徴があります。

---

利用例

AONT方式はすでにさまざまなサービスで利用されています。ここでは、その一部を紹介します。

• ZENMU Virtual Drive
  PCの社外持ち出しを安全に行うためのソリューション

ソリューション一覧

• TRUSTASサービス
  秘密分散法を利用するためのライブラリ

サービス＆ソリューション | リアルシス株式会社

---

処理方式

暗号化、復号、それぞれの処理方式を説明します。使用する記号は次のとおりです。

• E1
  平文を疑似メッセージに変換するための値を算出する処理

• E2
  𝑠+1個目の疑似メッセージを算出する処理

• E3
  疑似メッセージを暗号化する処理

• D3
  疑似メッセージに復号する処理

• 𝐾′
  E1で使用する鍵。乱数を用いる

• 𝐾0
  E2で使用する鍵。固定値でよい

• 𝐾
  E3、D3で使用する鍵

暗号化

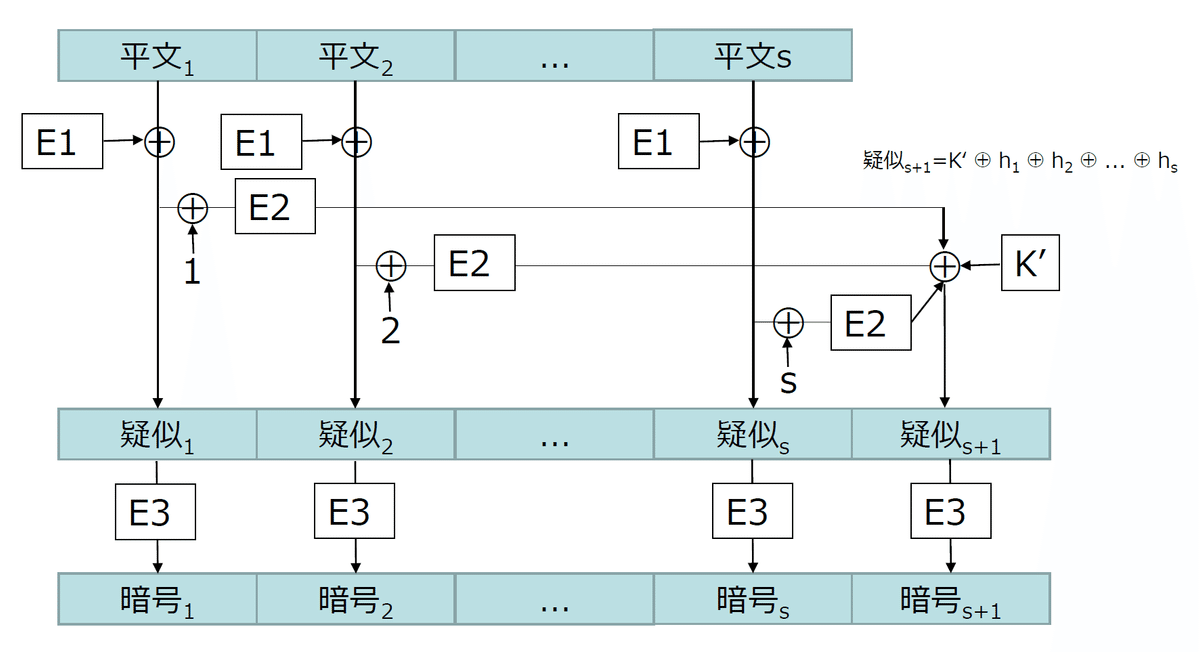
暗号化処理では、秘密情報である平文を固定長のブロックに分割し、まずブロックごとに処理を行って疑似メッセージというデータに変換します。次に、既存の暗号化処理を使って疑似メッセージのブロックごとに暗号化します。
ここでは、暗号化処理にブロック暗号 [3]の方式のうち、平文を𝑛ビットごとのブロックに分割し平文のブロックごとに独立して暗号化するECBモード（Electronic Codebook Mode）[4]を使用することとします。

暗号化処理の手順は次のとおりです。

1. 𝑠個の平文のブロックとE1で𝑠個の疑似メッセージに変換
   疑似𝑖 = 平文𝑖 ⊕ E1(𝐾′, 𝑖) (1≤𝑖≤𝑠)

2. １で変換した疑似メッセージをE2で変換
   ℎ𝑖 = E2(𝐾0, 疑似𝑖 ⊕ 𝑖) (1≤𝑖≤𝑠)

3. ２で変換したデータと𝐾′から𝑠+1個目の疑似メッセージに変換
   疑似𝑠+1 = 𝐾′ ⊕ ℎ1 ⊕ … ⊕ ℎ𝑠

4. 𝑠+1個の疑似メッセージのブロックをE3で暗号文に暗号化
   暗号文𝑗 = E3(𝐾, 疑似𝑗) (1≤𝑗≤𝑠+1)

暗号化処理 [5]

復号

復号処理では、まず暗号化されたブロックごとに疑似メッセージに復号します。次に、疑似メッセージのブロックごとに処理を行って平文に変換します。

復号処理の手順は次のとおりです。

1. 𝑠+1個の暗号文のブロックをD3で疑似メッセージに復号
   疑似𝑗 = D3(𝐾, 暗号文𝑗) (1≤𝑗≤𝑠+1)

2. １で復号した疑似メッセージをE2で変換
   ℎ𝑖 = E2(𝐾0, 疑似𝑖 ⊕ 𝑖) (1≤𝑖≤𝑠)

3. ２で変換したデータと𝑠+1個目の疑似メッセージから𝐾′に変換
   𝐾′ = 疑似𝑠+1 ⊕ ℎ1 ⊕ … ⊕ ℎ𝑠

4. 𝑠個の疑似メッセージのブロックとE1で平文に変換
   平文𝑖 = 疑似𝑖 ⊕ E1(𝐾′, 𝑖) (1≤𝑖≤𝑠)

復号処理 [5]

疑似メッセージから平文に変換するためには𝐾′が必要ですが、

の式を変形すると、

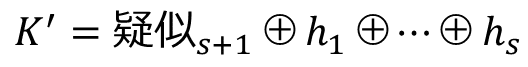
となり、疑似メッセージのすべてのブロックがないと値が求められないため、すべての暗号分のブロックを復号して疑似メッセージを求める必要があります。

---

安全性

安全性の確認のため、既知平文攻撃（Known-Plaintext Attack）を受けた場合にECBモード単独の処理とAONT方式の処理における復号処理コストを比較してみます。
既知平文攻撃とは、充分に多い平文とそれに対する暗号文のペアが得られるという環境における暗号解読方式です。[6]

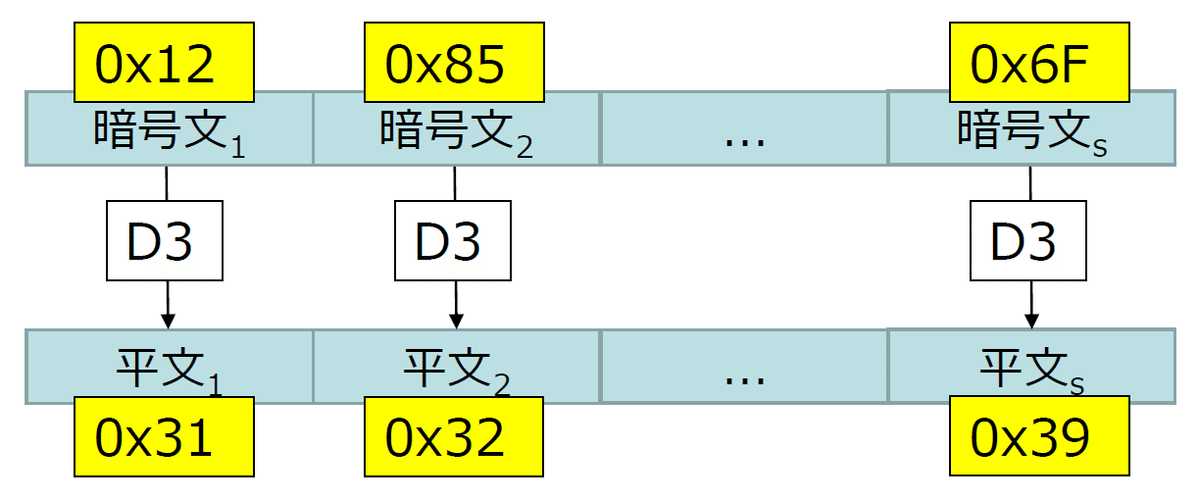
ECBモード単独の処理

平文が「0x39」でその暗号文が「0x6F」のペアを保有している状態において、暗号文「0x85」に対する平文を解読してみます。
既知の平文に対する暗号文が分かっているので、既知の１つのブロックに対する総当たり攻撃（Brute-Force Attack）でその鍵𝐾を求めることができてしまいます。
鍵𝐾が求められれば、暗号文「0x85」に対する平文が解読できます。

ECBモード単独の暗号文の解読

AONT方式の処理

平文が「0x7A」でその暗号文が「0x6F」のペアを保有している状態において、暗号文「0x85」に対する平文を解読します。
既知の平文に対する暗号文が分かっていますが、総当たり攻撃（Brute-Force Attack）で求められるのは疑似メッセージのみであり、どれが正しいかどうか判断できません。
そのため、すべてのブロックにおいてすべての鍵𝐾のパターンで疑似メッセージを生成し、

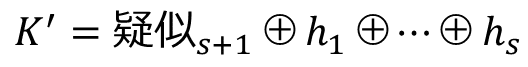
で鍵𝐾′をそれぞれ求め、下記の式が当てはまるかどうかを試行する必要があります。

AONT方式の暗号文の解読

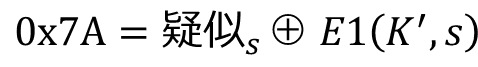
例えば、暗号化処理にDESの40bit鍵を使用して１ブロックが64bitのAONT方式で暗号化された8MBのメッセージが漏洩した場合、攻撃者は１つの40bit鍵候補をテストするために8MBのファイル全体を復号する必要があります。
通常のECBモード単独の暗号文を解読するコストと比較すると、8MBは67,108,864bitであり、１ブロックが64bitであるため、D3の処理回数において67,108,864 / 64 = 1,048,576倍のコストがかかります。
1,048,576は2^20であるため、2^40 x 2^20 = 2^60となり、攻撃者にとっては、40bit鍵の代わりに60bit鍵を破るのと同程度のコストがかかることになります。[1]
よって、AONT方式はECBモード単独よりもブロック数分安全性が向上することになります。

---

まとめ

• AONT方式は、暗号に対する様々な攻撃（総当たり攻撃、選択平文攻撃、関連平文攻撃、差分攻撃）に対する安全性を高めるための方式である

• AONT方式では、ブロックが１つでも足りないと復号することができないという特徴がある

• AONT方式は、シェアの合計サイズが秘密情報とほとんど同じという特徴がある

いかがでしたか？
AONT方式は、既存の暗号化処理と組み合わせることで簡単に安全性を強化していることがお分かりいただけたでしょうか？

アルゴリズムや安全性などについてさらに詳しく知りたい方は参考文献を参照してみてください。

---

参考文献

• [1] R.L. Rivest, "All-or-Nothing Encryption and the Package Transform", MIT Laboratory for Computer Science, 1997.

• [2] Adi Shamir, "How to Share a Secret", Massachusetts Institute of Technology, 1979.

• [3] 電子情報通信学会知識ベース, "1章 ブロック暗号", https://www.ieice-hbkb.org/files/01/01gun_03hen_01.pdf

• [4] 電子情報通信学会知識ベース, "3章 暗号利用モード", https://www.ieice-hbkb.org/files/01/01gun_03hen_03.pdf

• [5] Valér Čanda and Tran van Trung, "A New Mode of Using All-Or-Nothing Transforms", Institute for Experimental Mathematics, University of Essen, October 23, 2001.

• [6] 森井昌克, "WEPから読み解く暗号と安全性", "暗号解読とストリーム暗号", https://thinkit.co.jp/article/834/1