ビンゴの穴が全部あくまで何回？

初めまして！理系大学生のやおきです。
お正月に親戚皆でビンゴの穴を全部開けるとボーナス景品がもらえるという、+αビンゴ大会を行いました。
その時に「ビンゴが全部開くまで何回かかるんだろう？(数字を読み上げる回数)」と思い計算してみることにしました。
大学入試にありそうな感じの問題です。
正月ボケの頭の体操にちょうどよかったので、できそうな方は先に自力でぜひ挑戦してみてください。

前提

・ビンゴカード
ビンゴカードの5×5のマス目には、真ん中に柄、他のマスに数字24個が書かれています。
数字は1~75のいずれかの数字が書かれています。
1~75を15ずつ、5グループに分けた時、各グループから5つの数字を選び各列に配置します。これが今回用いたビンゴカードです。

ビンゴカード

・知りたいこと
ビンゴで全ての穴(24個)を開けるのに何回数字を読み上げる必要があるのか？

理論値計算

まずは、ビンゴの穴が全部開くまでの理論値を計算してみます。
・考え方
ちょうどn回目に全部の穴が開く確率を考えましょう。
　まずは、ちょうどn回目に全て開く場合の数を考えます。
n回目に出る数字は、ビンゴカードのいずれかなので24通り。
残りの23枚が開くタイミングをn-1回の中から選び(n-1 C 23)、並べます(23!)
→n-1 P 23。
他のタイミングではビンゴカードに無い数字が選ばれるので、75-24 P n-24。
よってちょうどn回目に全て開く場合の数は、24 × (n-1 P 23)×(51 P n-24)となります。
　次に、全体の場合の数を考えます。75枚からn枚選んで並べれば良いので、場合の数は、75 P nとなります。
　よって求める確率は、[ 24 × (n-1 P 23)×(51 P n-24) ] / [ 75 P n ]。
k P m = k! / (k-m)! を用いて整理してやると、[ 24×51!×(n-1)! ] / [ 75!×(n-24)! ]
となります。

続きは手計算がちょっと大変なのでPythonに計算してもらいましょう。
n回目に初めて開く確率は以下のグラフの通りになりました。

理論値計算結果

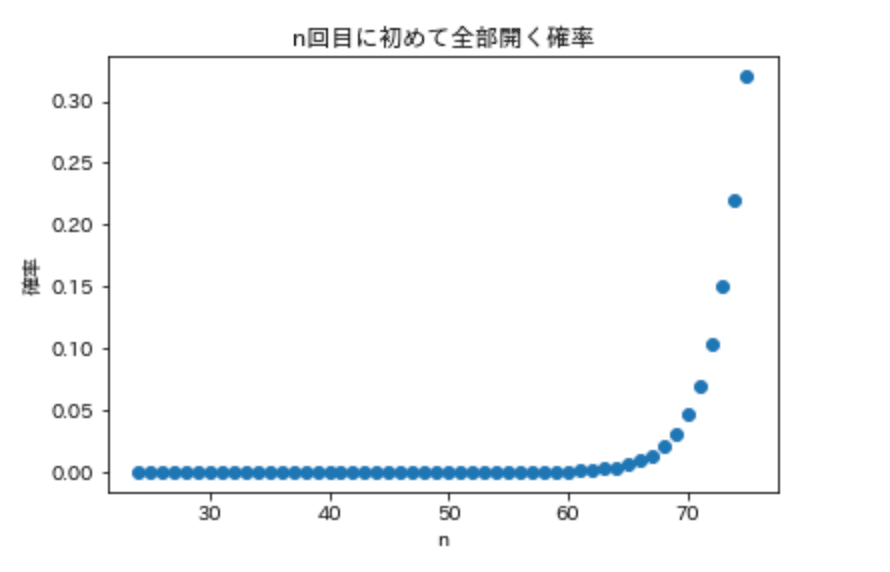
この確率を使って全て開くまでの平均回数と標準偏差も求めてみましょう。
平均回数：72.96回
標準偏差：2.39回

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib

#階乗
def factorial(n):
    ans = 1
    for i in range(n):
        ans *= i + 1
    return ans


f51 = factorial(51)
f75 = factorial(75)

#n回目に初めてビンゴの穴が全部開く確率
def p(n):
    return 24*f51*factorial(n-1)/factorial(n-24)/f75

#n回目までにビンゴの穴が全部開く確率
def sum_p(n):
    sump = 0
    for i in range(n):
        sump += p(i+1)
    return sump

vfactorial = np.vectorize(factorial)
vp = np.vectorize(p)
vsum_p = np.vectorize(sum_p)

n = np.arange(24,76,1)

#平均回数,標準偏差
mean = 0
mean2 = 0
for i in range(75-24+1):
    k = 75 - i
    mean += k * p(k)
    mean2 += k * k * p(k)

print('mean:{}回'.format(mean))
print('std:{}回'.format(np.sqrt(mean2 - mean**2)))

シミュレーション

おまけですが、シミュレーションで計算があっているか確かめてみます。
10000回ビンゴを行い全部穴が開くまでの回数を記録しました。
そのヒストグラムと平均値、標準偏差です。
平均73.13回、標準偏差2.23回なので上の計算と近しい結果となりました。
分布も理論値の方と似たような形になっています。

シミュレーション結果

#ビンゴ全部開けるシミュレーション
import numpy as np
import time
import matplotlib.pyplot as plt
import pandas as pd

#試行回数
N = 10000


#穴を開ける順番
bingo = np.arange(1,76,1)

#重複のないrandint
def random_int_nodup(min,max,num):
  ans = []
  i = 0
  while i < num:
    r = np.random.randint(min,max)
    if r not in ans:
      ans.append(r)
      i += 1
  return np.array(ans)

#全部穴が開くのにかかった枚数
all = []

for j in range(N):
  np.random.seed(int(time.time()))
  #ビンゴカードの生成
  b = random_int_nodup(1,15,5)
  i = random_int_nodup(16,30,5)
  n = random_int_nodup(31,45,4)
  g = random_int_nodup(46,60,5)
  o = random_int_nodup(61,75,5)

  #穴を開ける順番
  np.random.seed(int(time.time()))
  np.random.shuffle(bingo)

  #穴の数
  h = 0
  #番目
  k = 0
  #ビンゴ
  while h < 24:
    if bingo[k] in np.concatenate([b,i,n,g,o]):
      h += 1
    k += 1

  all.append(k)


all = np.array(all)


#可視化
print(pd.DataFrame(pd.Series(all.ravel()).describe()).transpose())
plt.title('全部開くまでにn回かかる(ヒストグラム)')
plt.xlabel('n回目')
plt.hist(all,bins=np.arange(all.min(),all.max()+1,1))
plt.show()

感想

思っていたよりほとんど全て読み上げないと全部開かないんだなあ。
先行研究の1列ビンゴする回数分布よりずっと急峻な分布になりました。
間違いを見つけたらお知らせください！