見出し画像
Photo by lazy_planet

AI人材育成講座：Day3　統計入門

やんばる

どうもやんばるです。自分の復習としてAI人材育成講座の記事を書いています。前回の受講で足りなかったことの一つが講座の振り返りがあまりできなかったこと。それを今回は補うために記事を書いています。

数字は嘘をつかないが、嘘をつく奴は数字を使う

マーク・トウェイン

数字には解釈の余地が無いためロジカルな表現には不可欠だが、自分に都合の良い数字だけを持ち出し、見せることで、これが全てであり真実であると思わせることができてしまう。

統計学とは

主観や経験、感などをいっさい排除してデータだけから意思決定をする。そのため、誰もが標準的な意思決定をすることができる。統計学を学び使うことによって自分の発言に対する説得力が増していく。
そんな学問です。


データの持つ価値

アナログからデジタルに変えることで、試しにつくってみたり、やってみてどうなるかを行い、ローコストでデータを取ることができるようになった。デジタルはローコストで試行錯誤ができる。

統計を使用した意思決定

デジタル技術の発達により、データを安価で取得することができるようになった。ということは統計学を用いた意思決定がより身近になったことを意味している。

ここでDX人材育成講座で習った「EBPM」が思い出される。要するに統計学を用いてEBPMすることができるようになるのだ。

証拠（データ）にも基づく政策立案・意思決定

統計学の活用事例

講座のおすすめ書籍として紹介されたいたこちらの著書、「統計学が最強の学問である」の中でも特に印象に残っていた話であるが、１９世紀にロンドンでコレラが大流行して、これを統計学を用いて解決した話がある。

当初、コレラの原因は不衛生な街の環境にあると推測し、テムズ川に汚染物を廃棄した。この結果、さらに感染者が爆増した。そこでジョンスノウという医師は感染者宅を徹底的にまわり、話を聞きだし、２つのことなる水道会社の利用状況で、コレラの感染者死者数が極端に違う事実につきあたった。

水道会社Aは大量の汚染物をテムズ川に流した下流から取水しており、水道会社Bはその上流から取水していたのである。汚染物に原因があることは間違いではなかったが、コレラ菌を政府がテムズ川にまき散らし、それを水道会社Aが再度、ロンドンの家庭にまき散らしコレラがロンドン市内で爆増したのである。

ジョンスノウは主観にとらわれず、事実を集め、水道会社Aと水道会社Bの相関関係に気づき、コレラ大流行の原因を突き止めたのである。

統計学では主観的な経験や感覚にとらわれずに客観的状況を把握する観察力を身につける。まずは徹底的に情報を収集し、その中で相関関係、因果関係を見つけ出すことが重要になる。

中央値と平均値の違い


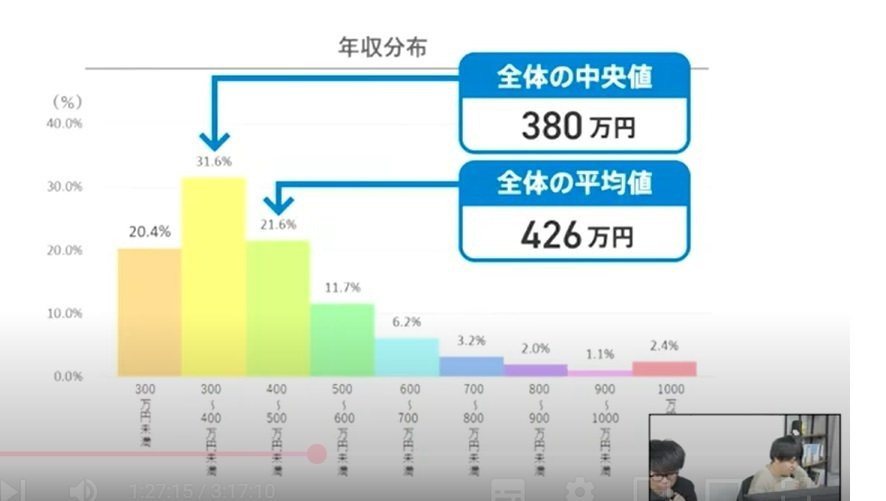
中央値はデータを小さい順または大きい順に並べたとき、真ん中に位置する値。データの真ん中に位置する値。 極端な値の影響を受けにくい特徴がある。。例: 5, 10, 15, 20, 100 の中央値は 15。外れ値が多いデータや偏った分布を持つデータに適している。

平均値とは、データの総和をデータの個数で割った値。１００人分のテストの点をを全部足してそれを１００で割った値。

平均値の罠
平均賃金をだす母集団の中に大谷翔平のようなスーパー金持ちがいたら、その集団の平均所得が一気に上がってしまう。そのためデータの雰囲気を掴みたい時には中央値を見るのがよい。
が対象的な二峰性データのときは中央値すらあてにならないので厄介です（例：高所得者と低所得者しかいない世界など）

実務で重要な統計手法

推定：一部のデータから全体を予測する。１０人のアンンケート結果を見て全体を予測する方法。選挙の出口調査などで使われる。

仮説検定：とりあえず仮説をたててデータで検証する。ＡＢテストなど。２つのWEBサイトがあってどちらがいいかをデータで判断する。気温が上がると弁当の売上が上がるという仮説をたてて、データをとって検証していく。

９５％信頼区間とは

95%信頼区間とは、あるデータから推定した範囲で「母集団の真の値がこの範囲に入る確率が95%」という意味です。繰り返し調査すれば、この範囲が真の値を含む割合が95%になること。

台風予測の天気図も９５％信頼区間が扱われている。 円の範囲で台風が動く可能性が95%で、外れる可能性が5%ということ。 先の予測になれななるほど予測が難しくなるので信頼区間の円が大きくなる。

統計に関するいろいろな手法がでてきたが、要するにデータ、事実、真実から判断、意思決定しましょうという話。

最後に重要ポイントとしてAIは関数であると説明があった。

AIは何かを入力して何かが出力される変換装置。関数は数字を入力して数字が出力される変換装置。統計も関数。AIはめちゃくちゃ入り組んだ関数であると。


いいなと思ったら応援しよう！