
LibreOfficeで正規分布曲線付きヒストグラム
LibreOfficeで、ヒストグラムを描くことはそれほど難しいことではありません。棒グラフを利用すれば、問題なく処理できます。
しかし、正規分布曲線を重ねて描こうとすると、これはちょっと面倒なことになります。以下、度数分布表と記述統計量を用いて描く手順を説明していきたいと思います。
度数分布表の入力
ある会社で、社員100名の一ヶ月の個人的な外食費を調査した結果、最大値は37053円、最小値は28604円、平均32035.75円、標準偏差2001.89円で、これを度数分布表に示すと、次のようになったとします。

これを、LibreOffice Calcに以下のように入力します。
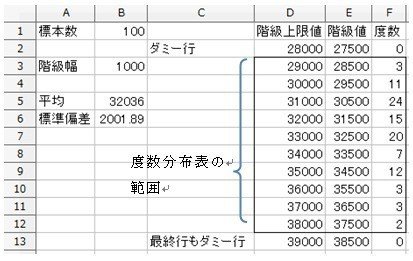
ここで注意してほしいのは、本来の度数分布の範囲の上下に度数が0のダミー行が1行ずつ設けられているところです。これは計算上は正規分布曲線のズレを少なくする意味と、後々作図のときの体裁に関係してきますので、必ず追加しておいてください。
階級値は、階級の上限と下限のちょうど真ん中の値ですから、この場合は、28500円、29500円……となり、階級値同士の幅は、当然ですが、階級の幅と同じく、1000円となります。
累積分布関数
これでヒストグラムは描くことができますが、正規分布曲線を描くことができませんので、その作図に必要な値を求めます。
まず、階級上限値を使って、累積分布関数の値を求めます。ただし、最後のダミー行(下の図中の①)は計算しません。例えば、[G2]のセルですと、
=NORMDIST(D2,$B$5,$B$6,1)
※カッコ内は、「数値」「平均」「標準偏差」「c(1で累積分布関数)」
という式が入っています。これを範囲いっぱいにコピーします。

最後に、正規分布曲線の値を求めます。
上限界までの累積分布関数の値と、1つ下の階級の累積分布関数の値の差に標本サイズをかけた値です。累積分布ですから、1つ下の階級の値との差を出せば、その階級のみの値になります。ただし、一番下の階級は、差を求める必要はないので、上限界までの累積分布関数の値に標本サイズをかけたもの、一番上の階級は、累積分布は全体が1ですから、1から最後の上限界までの累積分布関数の値(ここでは[G12]セル)を引いた値に標本サイズをかけたものを用います。
よって、[I2]には、
=G2*$B$1
[I3]には、
=(G3-H3)*$B$1
で、これを最後の1つ手前の行までコピーします。
最後のダミー行である[I13]には、1までの残りなので
= (1-G12)*$B$1
という式が入っています。
折れ線で作図
これで、必要な数値の算出が終わったので、作図の手順に入ります。
ここでは、グラフ機能のうち、線(折れ線グラフ)を使います。

・[グラフウィザード]から、[グラフの種類の選択]で、[線]の中の[線のみ]を選ぶ。
・[線の種類]から[平滑化曲線]を選ぶ。
・[データ範囲]に、度数分布表に上下のダミー行を含んだ[E2]から[F13]までを指定する。
・[データ範囲]に、「正規分布」の値(ここでは[I2]から[I13])を追加する。
そうすると、次の図のようになります。

次に、度数分布の部分を線からヒストグラムに変更するのですが、別種のグラフを重ねることができない(「縦棒と折れ線」グラフでは、棒グラフと折れ線は重ねられるものの、折れ線の平滑化ができない)ので、別の方法をとります。
Y誤差でヒストグラム化
グラフを編集モードに切り替えて(グラフ上で右クリック→[編集])、「度数」の線を選択して、[Y誤差範囲を挿入]を選びます。ひとまず、色を任意のもの(ここでは赤)に変更して、一旦[OK]を押します。

次に、「度数」の線を選択した状態で、[データ系列の書式]を選択して設定をします。

・[線の属性]の[スタイル]で[なし]を選択。
・[アイコン]から[シンボルなし]を選択。
これで「度数」の線が消えます。「Y誤差範囲」の設定を中途半端なまま、こちらの設定を行ったのは、①先にこちらの設定を行うと、「度数」の線を選択しづらくなって、「Y誤差範囲」を挿入しにくい、②先に「Y誤差範囲」を挿入してしまうと、「度数」の線を選択しづらくなって、線とアイコンを[なし]にしにくい、という2つの理由によります。
「度数」の線が消えるので、続いて「Y誤差範囲」の設定を行い、「Y誤差範囲」が「度数」を表せるようにします。
・「Y誤差範囲」を選択し、[Y誤差範囲の書式]を選択して、設定ダイアログを開く。

・[Y誤差範囲]のタブを選択。
・[誤差の種類]を[定数値]に設定。
・[誤差範囲の表示]を[負]に設定。
・[パラメーター]の[両方に同じ値]のチェックをはずし、[負]に最大度数以上の値を入力。
これで0から各度数まで[Y誤差範囲]の線が引かれます。
後は、体裁を整えます。
・「凡例」を削除。
・「正規分布」の線の[データ系列の書式]を開き、線の色と太さを調整。
・「Y誤差範囲」の線の[Y誤差範囲の書式]を開き、線の太さを調整。
「正規分布」の線は色を黒、太さを0、「Y誤差範囲」の線の太さを1.3cmに設定すると次のようになります。

このグラフを見ると、最初に度数分布表の上下にダミー行を設けた意味が分かっていただけると思います。ヒストグラムを「Y誤差範囲」つまりエラーバーの太さで表現しているため、X軸の両側に空白を設けないと、バーがはみ出してしまうのです。
また、最初に述べたように、ダミー行まで確率分布を計算しておかないと、正規分布曲線が両端で大きくズレを生じてしまいます。
しかし、この方法ではズレを完全に回避することは難しいようです。
下のヒストグラムは「R言語」で描いたものです。Y軸が確率密度(この場合、10000倍すると度数に一致)になっていますが、ズレは分かっていただけると思います。

ちなみに、PSPPで描いたヒストグラムは次のようになります。

