【中高生のための「論文」入門】④実験計画の作り方

研究計画を立てる

研究に使える時間は少ない。
無駄にしている時間はないし、学生が行う研究の場合、壮大な実験は不可能である。

研究テーマの選定も関わってくるが、どのように実験を行うかが非常に重要な意味を持つ。

また、それと同時に、先行研究調査に割く時間も十分でありながら最小の時間を見込まなければ、自分自身の研究･実験のための時間を侵蝕してしまう。

最初の計画は非常に重要である。
実験に当たっては、以下の点に特に注意が必要である。

・１．先行研究に基づいた予備実験で確認する。
・２．実験が必要な要因を的確に抽出する。
・３．１つの実験で扱う要因は１つに限定する。
・４．実験群と対照群（統制群）を比較する。
・５．安全に配慮する。
・６．仮説をもって実験を行う（仮説検証）。

これらをスケジュールに落とし込んで、計画を立案することが必要である。

ただし、注意点の3については、実験を複雑化させないための制限であり、実際は、複数の要因が交互作用をもっている場合は、１つの要因だけの実験では、上手く行かない場合がある。たとえば、血圧抑制剤の効果が性別によって異なる場合、投薬群と統制群に分けるだけでなく、それぞれを男女に分けて４群を設けていないと、正しい結果がでない。

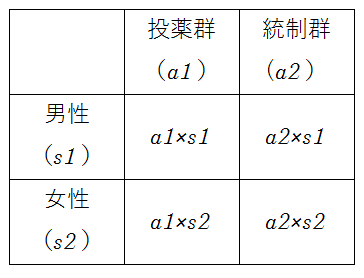
しかし、この場合でも、要因１つずつが対比できるようになっているという点では注意点3はある意味では守られているとも言える。

実験配置法

ある要因についていくつかの水準――たとえば、イースト菌による発酵実験で水温が、10℃、20℃、30℃、40℃の４つ――での比較実験を考える場合、実験条件が重要になってくる。

このような実験の場合、各水準について複数の実験を行うべきであり、本来はそれぞれが実験の要因以外は全くの同一条件でなければならないが、それは現実的には不可能である。こうした不可避の環境条件の違いによって生じる影響を「実験誤差」と呼ぶ。
この「実験誤差」が不可避であるのであれば、各実験において「実験誤差」を「公平」生じさせようというのが「実験配置法」という考え方である。

その方法は、実験順序を無作為化、確率化することによって、「実験誤差」も確率変動するものに変換し、統計的方法を適用した解析を可能にする、というものである。

この「実験配置法」については、「完全無作為化法」「乱塊法」「ラテン方格法」などがある。

話を単純にするため、ここでは要因を１つに絞って話を進める。
ある要因について、水準数ａで、各水準に付いてｎ回の実験を行うとすると、全体ではａ×n回の実験を行うこととなる。
この場合、得られるデータには水準・繰り返しの順に添え字をつけて、以下の表のように表す。

「完全無作為化法」とは、このａ×n回の実験をすべてランダムに行う方法である。つまり、x_11からx_anまでに乱数で数値をわりあてて、その順に実験を行うのである。

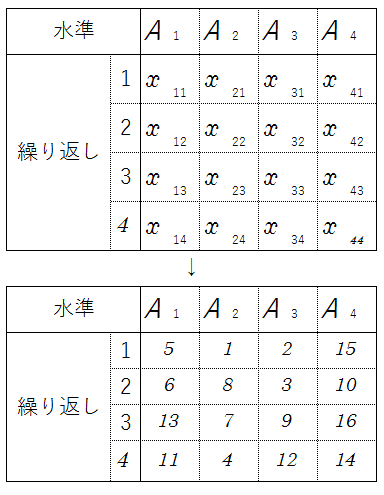
たとえば、４水準で繰り返し数が４回出会った場合、上の表のように順番をランダムに割り振るのである。

「乱塊法」は、環境条件が同じようなブロックを作って、その中で実験順序をランダムにする方法である。
「完全無作為化法」では、先ほどの例では2回目と3回目、5回目と6回目、7回目と8回目、14回目と15回目と16回目で同じ水準の実験が連続することになる。もし時間や日で区切って4サイクルで実験を行う場合、同じ水準の実験を同じような環境条件のもとで実施することになってしまう。
「乱塊法」はそれを避けるための方法である。

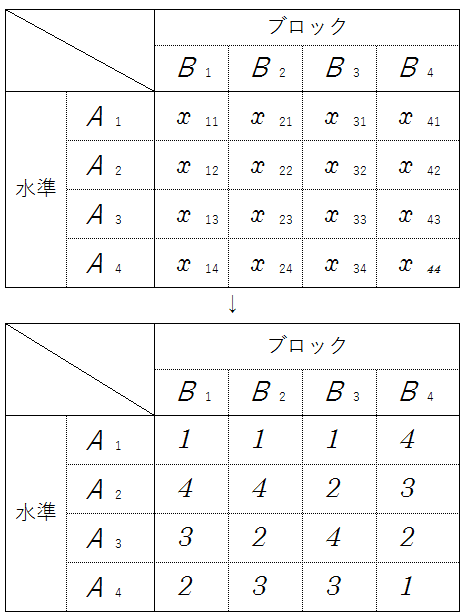
たとえば、上の表のようになる。

しかしこの場合、水準A1がブロック1から3までで1回目など、ブロック内で同じ順番になっているケースがいくつか見られる。

これを解消するのが、「ラテン方格法」である。
「ラテン方格法」を理解するには、「ラテン方格」を理解しなくてはならない。「ラテン方格」とは、n行×n列の方格にn種類の数値を、どの行どの列にも必ず１回ずつ現れるようにならべたものである。

ここの例の場合、水準が４つであるので、４×４の方格を作ってそこに４水準が必ずどの行どの列にも１回ずつ現れるように並べるのである。つまりブロックを２種類（この場合は時間ないし日と実験順序）想定するわけである。
たとえば、以下の表のようになる。

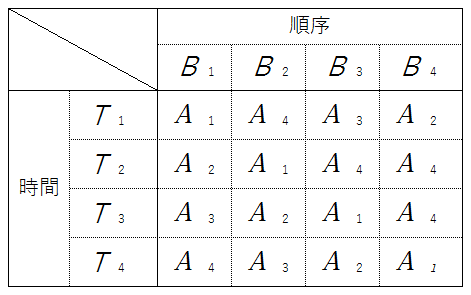
しかし、「ラテン方格法」は、要因水準数と２つのブロック内の要素の数が一致しなければならないという点で制約が多いため、適用することができる場面はそれほど多くない。
そのため、「完全無作為化法」か「乱塊法」のいずれかが用いられることがほとんどである。

要因の数や水準の数が増えると、組み合わせが複雑になり、実験数も増えてしまう。たとえば５要因で各２水準の場合、２の５乗で３２種類の実験が必要になる。

これを効率化するためには、「直交配列実験」という方法が用いられることが多い。この方法だと、実験の種類は３２から８にまで減らすことが可能である。
しかし、ここではその内容には触れない。大学の「実験計画法」の講義などで触れることになるだろう。

実験計画書

先に述べたような点を、考えながら研究の計画を立てたら、実験計画書にまとめておく。

一人での研究は勿論、複数人での共同研究となれば、研究の目標や計画の共有は極めて重要になる。
googleカレンダーなどのスケジューラーを使って、締め切り日などを管理すると良いだろう。

【参考文献】

・小泉治彦『理科課題研究ガイドブック第３版』（千葉大学先進科学センター，2015）
・鷲尾泰俊.実験計画法入門.改訂版,日本規格協会,1997,297p.
・大阪府立泉北高等学校総合科学科.課題研究マニュアル.大阪府立泉北高等学校総合科学科,2017