宇宙島へ１４「朝食は地球を見下ろして」

「宇宙エレベーター」を「クライマー」で昇っていくと、窓の外に見える水平線がだんだんと丸みを帯び、やがて地球全体が視野の中に納まるようになってきます。そしてその地球の姿も静止衛星軌道ステーションに近づくにしたがって益々小さくなっていきます。

では、この地球の見え方の変化を数式で見てみましょう。

高度による視点の変化で、地球の見える範囲がどう変わるのかを考えてみます。

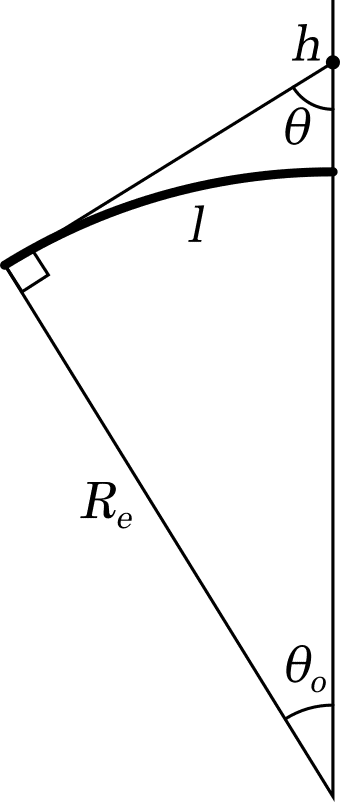
もっとも、空気の屈折によって光が直進せずに地空の湾曲に沿って回り込むように進むため、この計算で求めるよりも実際にはもう少し遠くまで見えることになります。
また、視野の中心から水平線までの角度θは、逆三角関数arcsinを用いて、以下の式で求めることができます。

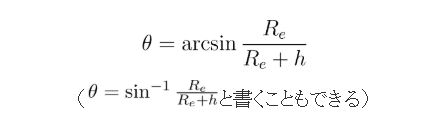
よって、2θがhを中心にした水平線から水平線までの角度ということになります。
一方で、人間の視野角全体は水平方向が約200度、垂直方向が下方75度と上方50度で合計約125度であるといわれます。
ですから、2θが200度以上の場合、水平線は全く視野に入らないという計算になります。

ただし、眼球の構造や視覚胞の分布の関係で，人間の視野は中心ほど分解能が高く、また注意も向けやすいようになっており、そのため視野は何重かのいびつな同心円状に分割されていると考えることが出来ます。

情報を捉える能力に優れている有効視野は水平方向が30度、垂直方向が20度程度のごくかきられた範囲だけです。注意力が比較的及びやすい安定注視野でも水平方向は60からせいぜい90度，垂直方向は45～70度程度と言われています。ですから、少なくとも2θが安定注視野の範囲をカバーできていれば、目の前はすべて地球と感じることでしょう。

旅客機は高度約約33000フィート、つまり約10000m上空を飛行しています。10000mは10kmですね。これで、どれくらいの距離が見えるかを計算してみましょう。

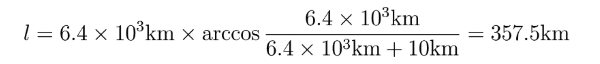
約360km先まで見えていることになります。

前回例にあげた「体重70kgの乗客が高度500kmにいるとき」についても計算してみましょう。

ということになります。「宇宙エレベーター」は赤道上に位置してみますから、θ=22°ということですから、南北については北緯22度から南緯22度までの範囲を見渡すことができるということです。このときの地球の大きさは、直径30cmのボールを約140cmはなれてみた場合とほぼ同じです。

人間の一番よく見える範囲が水平方向が30度、垂直方向が20度程度ですから、いかにも地球が見えたと感じられるであろう範囲をθ=10°として、高度を求めてみましょう。

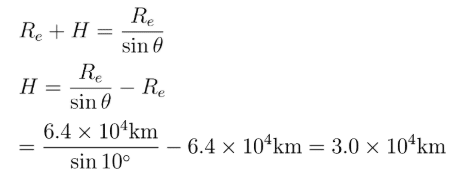
高度約30000kmまで達すれば、視野の中心に地球の全体を捉えることができます。

では、「宇宙エレベーター」に乗っていけば、面している地球の半球全体を視野におさめることができるのでしょうか。

アルツターノフの構想での先端である高度60000kmの宇宙ステーションまで行ったとしても、θ０は約84.1度にしかならないので北極点と南極点は視野には入りません。
これは逆に言えば、北極点と南極点からは「宇宙エレベーター」が見えないということでもあります。そうすると、北極点と南極点と「宇宙エレベーター」は直接の通信ができないということになります。

ちなみに高度60000kmでも見えないわけですから、静止衛星軌道36000kmは当然見えません。つまり北極点・南極点とは静止衛星軌道上の通信衛星を使った中継通信も不可能です。ここで、日本の昭和基地はどうしているのかという疑問がでるかもしれませんが、昭和基地があるのは南極大陸の外縁で南緯69度00分22秒の地点ですから、衛星通信は可能です。

さて、宇宙空間ではどこまでもものがくっきりと見えるため距離感がつかみにくいのですが、ここまで学んでくれば、天体の実際の直径が分かっていれば、先ほどの計算を応用することで距離がつかめます。

たとえば、映画『スターウォーズ』には帝国軍の衛星型巨大宇宙要塞「デス・スター」が登場しますが、この直径はおよそ120kmと設定されています。
この「デススター」がθ=4°で見えたとすると、

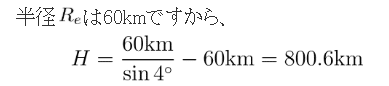
と、距離はおよそ800kmということが分かります。
また、同作品中で登場している巨大宇宙戦艦「スター・デストロイヤー」は全長がおよそ1kmあります。
この「スター・デストロイヤー」が「デススター」と同じ大きさに見えたとすると、どうでしょう。
この場合は球でないので、以下の形で近似して、おおよその距離がつかんでみましょう。

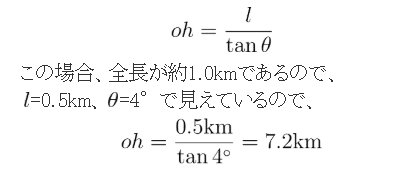
となります。

角度は器機を使えば測定できるでしょうが、それが無い場合に方法はないのでしょうか。

正確ではないですが、手を使っておおよその角度が測れることが経験的に分かっていて、天文観察や軍事の分野などで使われています。

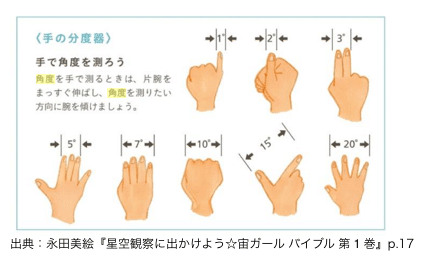
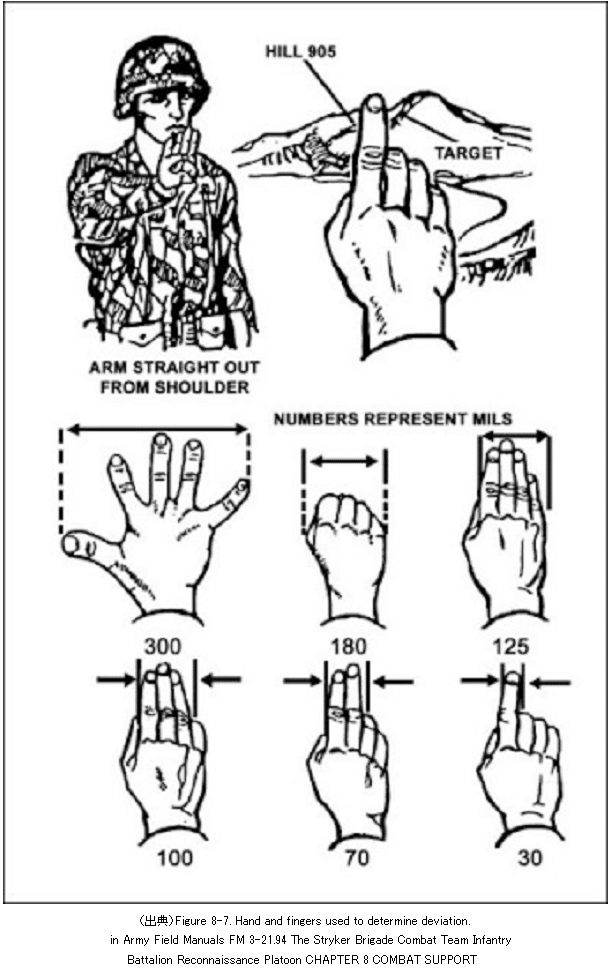
軍事関係ではmil(angular mil）という角度の単位が使われます。mil(angular mil）は、円周を6400に分割した角度単位で、1milはほぼ1km先の0.982mの幅の物体を見るときの視角にあたります。よって、対象までの距離（単位:km)は、対象の大きさ(単位:m) ÷ milで計算することができます。

【参考文献】
・石原藤夫・金子隆一(2009)「軌道エレベーター　宇宙へ架ける橋」早川NF文庫
・佐藤実（2016）「宇宙エレベーター その実現性を探る」祥伝社新書
・石川憲二（2010）「宇宙エレベーター−宇宙旅行を可能にする新技術」オーム社
・B・C・エドワーズ、F・レーガン、関根光宏（2013）「宇宙旅行はエレベーターで」オーム社
・佐藤実 (2011)「宇宙エレベーターの物理学」オーム社
・青木義男(2012)「宇宙エレベーター　人類最大の建造物」季刊大林53,p26-29
・大林組プロジェクトチーム(2012)「『宇宙エレベーター』建築構想　地球と宇宙をつなぐ10万キロメートルのタワー」季刊大林53,p30-59
・石川洋二(2012)「2050年宇宙エレベーターの旅」季刊大林53,p60-61
・読書猿(2016)「道具を使わず一瞬で離れた場所との距離を知る方法」（2019年4月17参照）