
【中高生のための「論文」入門】⑤研究の進め方
実験ノート
研究において、「実験」を行う場合、その結果は勿論、方法や実験の状況についても、詳細に記録を残しておく必要がある。

通常研究においては、研究一つごとに「実験ノート」を作成して、記録を残していく。個人研究ではその個人が、グループ研究ではそのグループで「実験ノート」を所有する。
記録を残すということは、失敗も含めて全てを残すということであり、この記録の改ざんは、研究上許されない。
また、気づきやアイデアなど、結果や方法以外のことも記載しておく。実験から思いついたという証拠となるからである。
書き方については、研究分野によって様々な違いがある。たとえば、数百人、数千人のアンケートデータを扱うような心理学分野では、集計データのすべてをノートに記録するのは現実的ではないので、記録とは言っても、実際のデータは書き込めない。
九州大学の中山敬一教授は、実験ノートの内容として、次の7点を挙げている。
1.タイトル
2.日付
3.実験目的
4.材料・方法
5.実際におこなった手技
6.結果
7.考察
このほか、守るべき共通のルールは存在している。
・ページ順序を後から入れかえられないものであること。
・表紙には、研究テーマと使用開始年月日および使用終了年月日、氏名を記入しておく。
・インクによって書かれていること。
・隙間を空けないこと(余白には「以下余白」と注記する)
・個人研究の場合は本人のみが記入すること。グループ研究の場合は記入者氏名を明記すること。
・書き間違えも消さないこと。
などである。
コクヨの「リサーチラボノート」など、専用の実験ノートも市販されているが、それにこだわる必要はなく、普通の大学ノートでも全く問題はない。
大学では研究室ごとに特定の実験ノートを使用していることがある(実験ノートは個人の所有ではなく、研究室の「財産」となることも多いため)。また、電子実験ノートのサービスも登場しているが、研究機関向けの商品なので、個人では使用しにくい。
データの取り扱い
実験データには、「定性的データ」と「定量的データ」がある。
たとえば、果物が熟していく過程を色の変化で記録した場合、それは「定性的データ」である。その色をスペクトル分析にかけて記録したとすると、それは「定量的データ」になる。
「定性的データ」を得る実験を「定性実験」、「定量的データ」を得る実験を「定量実験」という。
一般的に、研究の方向性としては「定性実験」から「定量実験」へ向かって行われる。しかし、「定量実験」は、現象のある側面だけに注目しているため、実験計画が適切でないと、現象の全体像が把握できなくなってしまう可能性がある。
また、定量実験には、様々な特殊な測定機器が必要となるケースも少なくないため、本講座で行うような個人的な研究では難しい場合があるので、注意が必要である。
さて、測定されたデータは、必ず誤差を含んでいる。測定機器も正確に測れるわけではないのである。最小表示以下については分からないのである。これは不可避のもので「偶発的必然誤差」と呼ばれる。
この誤差を最小限に止めるためには、常に測定機器の補正と点検が必要である。分解能の高い電子天秤では、重力加速度の影響を考慮して、使用する現地で校正が行われる。
また、測定者の癖などによって生じる誤差もあるため、グループ研究では、測定装置と測定者を一対一対応で固定しておくことが必要である。
この誤差の問題が、同じ実験を複数回行わなければいけないという理由の一つである。
数値を記す場合、理科系の研究では「有効数字」ということを考えて記録する。これは、単位を変えると、小数点の位置が変わってしまうため、「小数点第○位まで」という制限が意味を成さないためである。
「有効数字」は最上位の位から何桁目までが測定されているのかということで考える。たとえば、電子秤での測定が「100.0g」であった場合、可能性としては「99.95~100.04g」までの範囲が考えられる。そこで、「100g」とは記さずに、「100.0g」と記す。この場合有効桁数は「4桁」となる。指数を使って表す場合は、この有効桁数の数字×10の○乗で表す。そのため「100.0」は「1.000×10の2乗」となる。
測定値を用いて計算する場合には、有効桁数を考慮したルールに従わなければならない。
・加減算は、単位をそろえた上で、最も精度の低い数字にあわせる。
2.84g+4.3g=7.14g→7.1g
・乗除算は、最も桁数の少ない有効数字にあわせる。
4.9km÷1.22時間=4.0163…km/h→4.0km/h
ただし、途中では数値をそのまま用いて、最後で有効桁数を考えて表記するようにする。そうしないと、途中で計算をするたびに、誤差が大きくなっていくからである。
結果の可視化
実験や調査の結果をわかりやすく示すためには、表やグラフの活用が欠かせない。また、そうした資格化によって、より考察が行いやすくなる。
表の作成:実験で得られた多くのデータを整理し、簡潔に示すためには、表が有用な場合が多い。データの関係や傾向を分かりやすく示すためには、どのような観点でまとめるかというのが重要になる。また以下のような点に注意する。
・何の表であるのかが分かるようにキャプションをつける。
・各行には実験条件や分類を記載する。
・各列には測定項目がわ分かるように、見出しと単位を記載する。
・サンプル数、標準偏差、標準誤差などを記載する。

令和元年年における『日本企業等への就職を目的とした「技術」又は「人文知識・国際業務」に係る在留資格認定証明書交付状況について』 図5 職務内容別(法務省入国管理局)
グラフの活用:グラフを用いると、法則性や傾向を視覚的に分かりやすく示すことができる。 様々なグラフの種類があるが、それぞれに特徴があるため、何が示したいかという目的に応じた適切な種類のグラフを選択する必要である。
・円グラフ:各要素が全体に占める割合を示す。相対的な比較に用いることが多い。
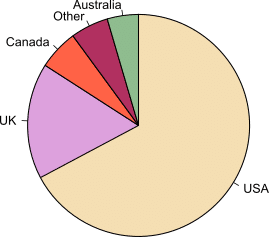
英語を母国語とする人の人口を表した円グラフ(wikipedia)
・棒グラフ:要素ごとの量を示す。量を比較する場合に用いることが基本であるが、縦軸に割合を取る場合もある。
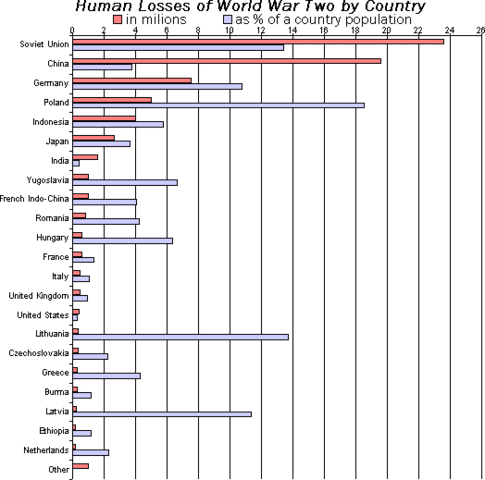
・折れ線グラフ:要素の時系列変化を示す。縦軸横軸共に基本的には連続量である。縦軸が結果を示す要素である。
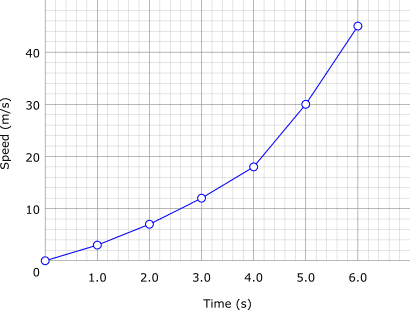
・散布図:二つの要素間の関係を表すのに用いられる。基本的には両要素とも連続量である。通常横軸が影響を与える要素、縦軸が影響を受ける要素である。
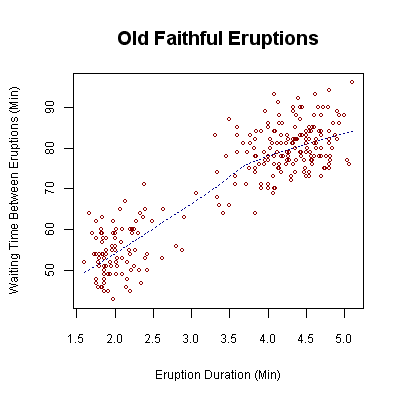
イエローストーン国立公園の間欠泉「オールド・フェイスフル・ガイザー」の噴出時間と間隔(wikipedia)
・ヒストグラム:連続データの階級別度数を示す。横軸が変数の幅(階級)、縦軸が度数であり、面積が階級の頻度を表す。
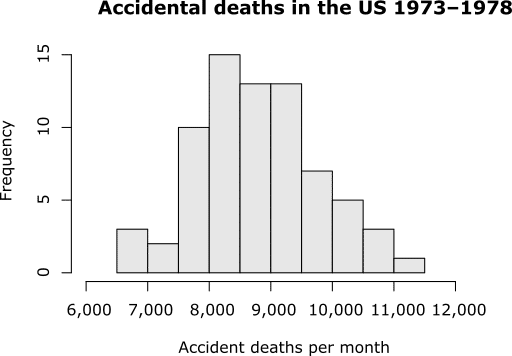
アメリカの事故死者数(1973-1978)(wikipedia)
【参考文献】
・中山敬一.“小保方リーダー&若手研究者必読!今さら人に聞けない「正しい実験ノート」の書き方”ダイヤモンド・オンライン.2014-04-23.https://diamond.jp/articles/-/52057(参照 2020-04-03)
・小泉治彦.理科課題研究ガイドブック,第3版.千葉大学先進科学センター,2015,81p.
・大阪府立泉北高等学校総合科学科.課題研究マニュアル.大阪府立泉北高等学校総合科学科,2017
この記事が気に入ったらサポートをしてみませんか?
