【中高生のための「論文」入門】⑥統計手法の具体例

はじめに

確率分布を使って、偶然かどうかを判断することを、確率統計学では「検定」と言う。

以下では、エクセルを使って、どのような計算を行って検定を行っているのかを説明する。「R」「Python」「Julia」などの言語や、「SAS」「PSPP」「JASP」などのフリーで利用できる統計ソフトを用いることができるのであれば、そちらを使うことには何の問題もなく、むしろ好ましい（統計については「文系がまとめたPSPPによる統計分析」にまとめてあるので参照）。

具体的な手法の選択については、白鷹増男.統計解析法の選択.日本食生活学会誌.2010. vol.21,no.1,p.3-6.を参照。

カイ２乗検定

カイ２乗検定は、統計の検定の中で、割合・比率を検定する方法である。

例題：男女別の賛成と反対
命題：男性の賛成5で反対15、女性の賛成が14で反対が6だった場合、男女で賛成反対に差があるといっていいか。

帰無仮説と対立仮説

まず、「差がないという仮説」と「差があるという仮説」を立てる。

「差がない」ということは、賛成反対の男女差は偶然だということである。「差がある」ということは、賛成反対の男女差は偶然ではないということである。「差がないという仮説」を「帰無仮説」、「差があるという仮説」を「対立仮説」と言う。カイ２乗検定では、帰無仮設を検証する。

この場合は、以下のようになる。

帰無仮説：賛成反対に男女差がない（偶然であり得る）
対立仮説：賛成反対に男女差がある（偶然ではありえない）

差があるかどうかを知りたいのに、どうして「差がないという仮説」を検証するのか。これは、「差がある」という状態には、「とても差がある」から「少しだけ差がある」までいろんな状態があるのに対して、「差がない」は、逆に言えば「どちらも同じ」という、１つの状態しかないため、分かりやすく確かめやすいからである。

カイ２乗という値を求めて、それがカイ２乗分布表で求めた限界値以上だと、帰無仮説が棄却され、対立仮説が採用される。つまり差があることになる。ただし、通常は5％の水準で検定するため、同じ検査を100回行った場合、5回は間違う可能性がある。

期待度数の計算

カイ２乗値を求めるためには、まず期待度数を求める必要がある。

クロス集計表の回りの合計をそれぞれa～eとすると、期待度数は次の表のようにして求める。

カイ２乗値の計算

観測度数が期待度数からどのくらいずれているかが「カイ２乗値」である。以下の式を使って計算する。

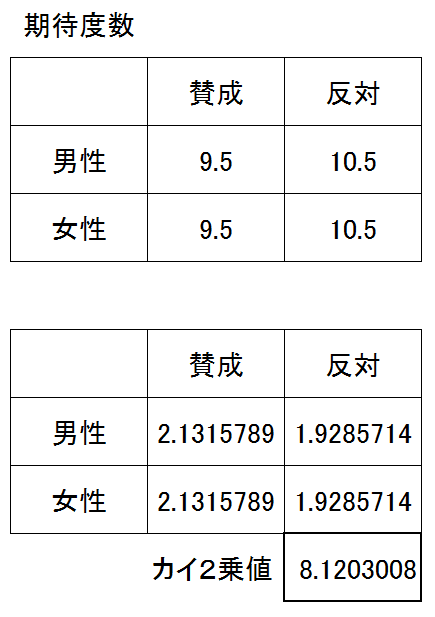
この場合、期待度数は男性女性ともに、賛成9.5、反対10.5となる

これを用いて計算すると、男性の賛成2.131、男性の反対1.929、女性の賛成2.132、女性の反対1.929で、カイ２乗値はこれらの合計で8.121となる。

カイ２乗値には、次のような性質がある。
・期待度数と観測度数が一致する場合、つまり、完全に差がない状態だと、カイ２乗値は0になる。
・ずれが大きくなると、カイ２乗値は大きくなる。
・カイ２乗値が大きいと、起こる確率が低くなる。つまり、大きいずれほど、起こりにくい。
・カイ２乗値の分布は「自由度」によって変わるということ。

自由度

自由度は、項目数引く１でもとめることができる。たとえば、支持・不支持の２つの調査なら、支持でなければ不支持なので、１つ決まればよい。もし、支持・不支持・どちらでもない、の３つだと、２つが決まるらないといけない。つまり自由に決められるのは、項目数引く１で、これを自由度という。ここのように、賛成･反対と男女の２要因ある場合はそれぞれの値をかける。
よってここでは、（男女の２項目-1）×（賛成反対の２項目-1）で自由度は1となる。

検定手順

期待値からのずれ、つまりカイ２乗値が、５％または１％という基準となる確率で起こる値aよりも大きいか小さいかを判断する。
カイ２乗値の確率分布は、たとえば図のようになっているので、ここではa以上の確率が、たとえば５％になっている。基準となる値aは、自由度ごとにカイ２乗値を記したカイ２乗分布表から求める。

たとえば、５％を基準とする確率で考えた場合、カイ２乗値が、基準となる限界値aよりも大きいということは、５％の確率、つまり100回検定すると5回しか起こらない検定結果が起こっている、と考える。つまり偶然ではない。
一方、カイ２乗値が、限界値aよりも小さいと言うことは、100回検定すれば95回起こりうる検定結果が起こっている、と考える。つまり偶然である。
偶然でないなら差がある、偶然なら差がないという判断になる。
ここでは、自由度が1、有意水準を0.05（5％）とすると限界値は3.8415である。

なお、EXCELでは、関数を用いて限界値を求めることができる。自由度1、有意水準0.05のばあい、以下のように記述する。

=CHISQ.INV(0.95,1)

ここでは、3.841458821…となる。

検定結果

カイ２乗値は上の計算から8.120。限界値は上の表から0.05（5％）水準で3.841。カイ２乗が、限界値より大きいので、帰無仮説が棄却され、対立仮説が採用される。よって、賛成と反対には男女差があると言える。
なお、EXCELでは、関数を用いてカイ２乗値から、有意確率（p値）を求めることができる。
カイ２乗値が8.120、自由度が1の場合、のように記述する。

=CHISQ.DIST.RT(8.120,1)

ここでは、0.004377956となり、0.05よりも小さいので、有意と判定され、帰無仮説が棄却される。

→【エクセルによるカイ２乗検定】

ｔ検定

互いに重ならない２群の平均値を比較して、２群に差があるかどうかを調べるのが、「対応のないｔ検定」である。ただし、基本となる「スチューデントのｔ検定」は同じような正規分布を描く２群にしか適用できない。これを、統計用語を用いて表現すると、以下のようになる。

正規分布で等分散が仮定される、対応のない２群の平均値に差があるかどうかを検定する検定が、対応のないｔ検定である。

ここでは、まず「スチューデントのｔ検定」の説明を行う。実際には「等分散の検定」を事前に行わなければいけないが、ここでは省略する。

手順としては、カイ２乗検定と同じで、帰無仮説を立てて、検定を行う。

ここでは、以下のような例題を例として考えてみる。
例題：クラス平均の比較
ある２つのクラスの算数のテストの結果は次のようになりました。この結果から、２つのクラスの成績に差があると言えるか。
１組 65, 50, 55, 60, 70, 50, 45, 60, 55, 70
２組 55, 70, 75, 45, 50, 70, 90, 95, 85, 90

帰無仮説と対立仮説

帰無仮説：２つのクラスの平均値に差はない
対立仮説：２つのクラスの平均値に差がある
※実際には等分散かどうかを検定する必要があるが、ここでは省略する。

統計では、観測された数値は基本的に、たまたま得られた結果と考える。テストの得点も、迷ってたまたま選んだ答えもあれば、単純なミスで不正解になったものもあるので、たまたまその得点になっただけとなる。

すると、個人の得点も本来はぶれがあるので、平均点も本当は誤差があるということになる。この誤差の幅を推定して、その誤差が重なっていなければ差があるということになる。

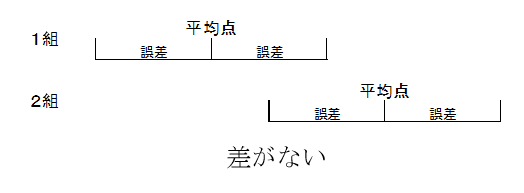
実際には、２つの平均値の誤差そのものではなく、平均の差の誤差を求めて検定する。数値で言うと、差の誤差の範囲に0が含まれば、差がない可能性があるということになる。

検定の手順

各個人の得点が平均からどれだけ離れているかを、平均との差で表す。これを偏差と言う。
たとえば、１組の平均は58なので、１組の一人目の偏差は65－58＝7。
これを全員分求めると以下のようになる。

各個人の偏差の２乗（同じ値同士かけたもの）を計算し、その合計を計算する。この合計を「偏差平方和」という。
たとえば、１組の一人目は偏差が7なので、偏差の２乗は49となる。
偏差平方和は、偏差の２乗を単純に全部足せばいい。

・平均の差、母分散の推定、差の標準誤差を計算する。
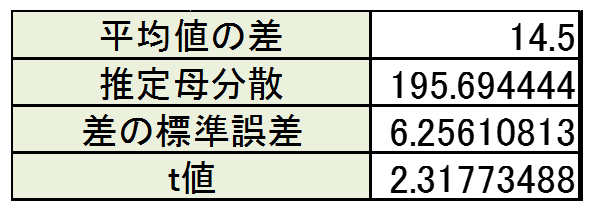
平均の差は、大きい方から小さい方を引く。
母分散は全体のデータのばらつきだと考えればよい。ここでは、２つの組の偏差平方和を足して、２つの組のデータの数から１を引いた数を足したもので割る。つまり次の式になる。

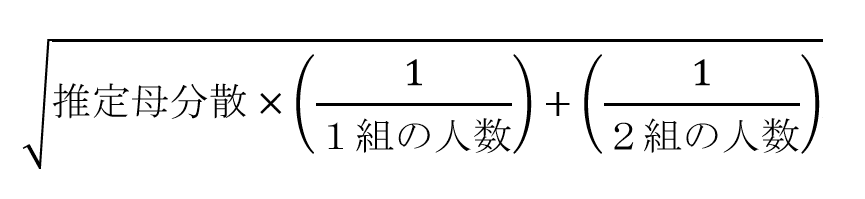
差の標準誤差は、推定した母分散を用いて求める。推定母分散に、２つの組のデータ数の逆数を足したものをかけた値の平方根がその値となる。つまり、次のように表すことができる。

ここでは、平均の差、母分散の推定、差の標準誤差は、それぞれ以下の値になる。

ｔ値を求める。その差が起こりうるかどうかを確かめるために用いる値で、カイ２乗検定におけるカイ２乗値にあたる。こうした、起こりうるかどうかを確かめるために用いる値を検定量という。
ｔ値は、平均の差を、差の標準誤差で割った値となる。つまり次の式で求めることができる。

ここでは、14.5/6.2561で割ればよい。

自由度から限界値を求める。自由度は２つの組のデータ数から１をひいた値同士を足したもの。ここでは、(10-1)+(10-1)=18となる。つまり、推定母分散を求めるときの分母。
この自由度を元に、ｔ分布表から限界値を求める。

ここでは、両側5％水準で検定を行うこととするので、両側0.05の列の、自由度18の行を見る。片側検定は「Aの方が大きい」あるいは「Bの方が大きい」と言えるかどうかを検定する場合、両側検定はどちらが大きいかは問題にせず差があるかどうかを検定する場合。

先ほど求めたｔ値が限界値よりも大きければ、対立仮説が採択され、限界値よりも小さければ帰無仮説が採択される。

なお、EXCELでは、関数を用いてｔ値を求めることができる。ここでは両側検定を行っているので、以下のように記述する。値は、2.10092204…となる。
=T.INV.2T(0.05,18)

結果

ここでは、限界値は2.101であり、ｔ値が2.318で限界値よりも大きいため、対立仮説「２つのクラスの平均値に差がある」が採択される。片側5％で検定しても限界値は1.734なので、差がある、つまり２組の方が平均値が高いと言える。

なお、EXCELでは、関数を用いて検定を行うことが出来る。

ここでは、ｔ値が2.318、自由度が18の両側検定なので、

=T.DIST.2T(2.318,18)

となる。有意確率（p値）は0.032…となり、0.05も小さいので、有意となり、帰無仮説は棄却される。

また、別の関数を用いれば、具体的な数値から直接できる。ここの検定の場合だと、以下のようになる。

「T.DIST.2T」関数を用いた場合と同じ「p値」となり、有意と判定できる。

等分散が仮定できない場合

２群に等分散が仮定できない場合は、「ウェルチのｔ検定」を用いる。現在では、等分散かどうかを問題にせずに「スチューデントのｔ検定」ではなく「ウェルチのｔ検定」だけを行うことが主流となっている。ｔ値と自由度に以下の式で求めた値を用いる。

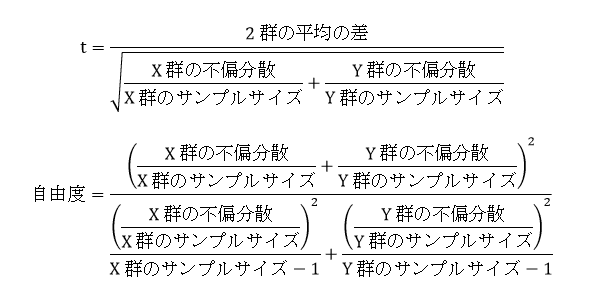
EXCELでは、「データ分析」ツールの「t-検定: 分散が等しくないと仮定した２標本による検定」で、「ウェルチのｔ検定」を行うことが出来る。

これでは、自由度を近似値の整数を用いており、上の式の値を用いて「T.DIST.2T」関数で求めた「p値」とは一致しない。

また「t.test」関数で最後のパラメータを「3」にすれば、非等分散の検定が行えるが、これも微妙に数値が一致しない。

対応のあるｔ検定

「対応がないｔ検定」があるのであれば、「対応のあるｔ検定」も当然存在する。「対応がある」とは、１つの集団について、平均の変化を比較するような場合を言う。
「対応のあるｔ検定」では、２つのサンプル「差の平均」と「差の標準誤差」（「差の標本分散」または「差の不偏分散」を用いて求める）から「ｔ値」を求める。

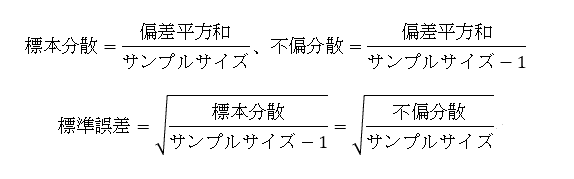
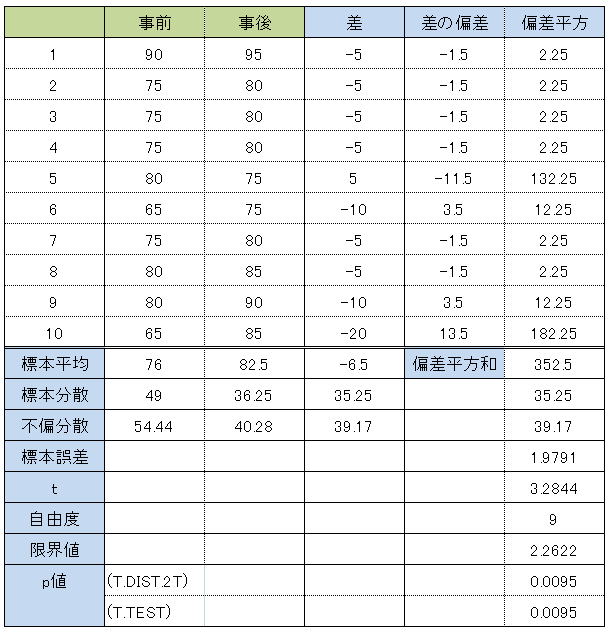
EXCELでは「T.TEST」関数を用いると、「対応のあるｔ検定」を行うことが出来る。

→【エクセルによるウェルチのｔ検定】

ブルンナー=ムンツェル検定

tudentのｔ検定は、等分散を仮定しているため、不等分散には対応できない。これに対応したのが、Welchのｔ検定である。

しかし、この2つのｔ検定葉は、分布の正規性を仮定しているため、正規性が仮定できない（ノンパラメトリックな）状況では、Mann-WhitneyのU検定が広く使われている。
しかし、Mann-WhitneyのU検定には、不等分散の状況ではうまく検定できないという欠点がある。

これらのすべての問題を解決し、正規性も等分散性も仮定しない検定として考案されたのがBrunner-Munzel（ブルンナー=ムンツェル）検定である。

→【エクセルによるブルンナー＝ムンツェル検定】

なお、ファイルはｔ分布を既存の関数で簡易的に計算しているので、統計言語「R」の関数「brunner.munzel.test」とはp値が微妙に異なる。

【参考文献】

・Brunner,Edgar. Munzel,Ullrich.The nonparametric Behrens-Fisher problem: Asymptotic theory and a small-sample approximation. Biometrical Journal.2000,vol.42,no.1,p.17-25.
・奥村晴彦.“Brunner-Munzel検定”.奥村研究室.2019-04-10.https://oku.edu.mie-u.ac.jp/~okumura/stat/brunner-munzel.html（参照 2020-04-06）