[PSPP]因子分析②斜交回転

斜交回転

斜交回転は因子間の相関が想定される場合に用いる手法です。より正確には、相関があってもかまわないという手法です。それは先ほどのプロットを元に説明すれば、縦軸と横軸を別々に回転させるということになります。

ここでは、手順と結果の違いが良く分かるように。先ほど直交回転で用いたデータを使って、斜交回転での分析を行ってみましょう。

手順は、シンタックスエディタを開いて、変更を加えるところまでは同じです。

違うのは、

・最後の行を「/ROTATION=PROMAX.」に変更。

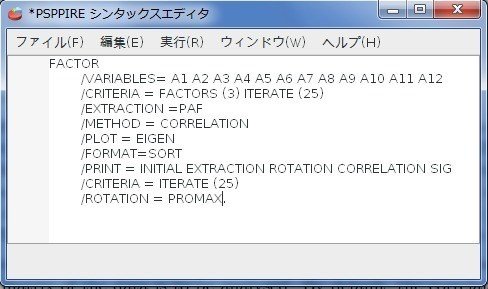
という１手順が［実行］→［すべて］を選択の前に入るだけです。なお「PROMAX(k)」という形で、k（カッパ）値を指定することもできますが、指定しなくてかまいません（指定しない場合は5になっています）。

出力の見方

最初に出力されたのはこちらも「相関行列」。これは直交回転と変わるところはありません。

次の「共通性」も直交回転とまったく同じです。

「説明される分散の和」では、「回転後の負荷量の平方和」だけが、直交回転と異なっています。これは斜交回転では寄与率を計算することができないためです。

その他の値は、直交回転と同じです。

キャプチャーを載せませんが「スクリープロット」もまったく同じものが表示されます。

因子行列は直交回転とはことなり、３つ出力されます。

上から(ここでは左から)順に、「因子行列」「Pattern Matrix（パターン行列）」「Structure Matrix（構造行列）」となっています。

直交回転の「回転後の因子行列」にあたるのは、プロマックス回転では、「パターン行列」です。よって、解釈や因子分析表への記入には、「パターン行列」を用います。

最後に「Factor Correlation Matrix（因子相関行列）」を見ます。ここで相関が「0」の場合、直交回転でもう一度分析するといいでしょう。

分析結果を表にまとめると、例えば次のようになります。

この場合、第２因子のA11・A9・A10・A12が負になっていますが、全部が負なので、あまり問題はありません。1つの因子の中に負の負荷率のものが入っていると、それは逆転項目として扱います。

たとえば、因子分析の項目の中に「勉強したい」「遊びたい」「テストを受けたい」という３つがあったとすると、おそらく「遊びたい」は負荷量がマイナスになるはずです。「勉強したい」「テストを受けたい」にそろえるためには「遊びたくない」にしなくてはいけませんよね。そこで、質問とは反対の内容を聞きたい項目として、数値を逆転して分析をします。

最後に。結果の表を直交回転のときと比べると、共通性と因子寄与がありません。この２つは斜交回転では記入する必要はありません。

斜交回転をするということ

斜交回転をするのも、直交回転と目的は同じです。違うのは、縦軸と横軸をそれぞれに回転させるところです。

すると、軸が直角ではなく斜めに交わることから「斜交回転」と呼ばれます。

もしも、この軸が直角に交わることになると、因子間の相関が「0」になります。その場合は、直交回転と結果的には同じになります。

つまり、斜交回転は因子間に相関を仮定しているが、結果的には相関がなかった場合でも分析できるのです。

因子分析を行う場合、直交回転よりも斜交回転を優先した方がいいという意見があるのはそういうわけです。