LibreOfficeで正規確率プロット

正規確率プロットには、正規Q-Qプロットと正規P-Pプロットの２つがありますが、ここで描くのは、正規Q-Qプロットの方です。

正規Q-Qプロットは、Ｘ軸には観測された値つまり実際のデータの値を、Ｙ軸に観測された値が正規分布に従う場合の期待値をとった確率プロットです。

プロットが直線に近ければ近いほど、観測値は正規分布に近いと考えることができます。

先に説明したとおり、正規Q-Qプロットは、Ｘ軸には観測された値つまり実際のデータの値を、Ｙ軸に観測された値が正規分布に従う場合の期待値をとった確率プロットです。よって、必要な数値の算出もそれほど難しくなく、比較的簡単にLibreOfficeで描くことができます。

数値の算出

まず、標本サイズ（N）と平均、標準偏差を計算しておきます。

次に、データの順位を算出します。

上の図のように、例えば[D2]セルですと

=RANK.EQ(C2,C$2,C$101,1)　 ※カッコ内は順に「数値」「範囲」「順序（1=昇り順）」

と入力します。下のセルはこのセルをコピーして貼り付けています。「RANK.EQ」関数は、同じ数値があった場合、最も高い順位を表示します。つまり、昔のエクセルでRANK関数とされていたものと同じです。

次に確率を計算します。

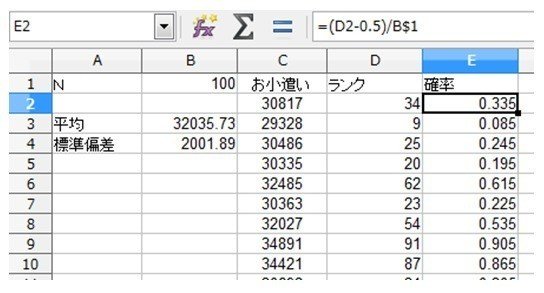
[E2]セルには、

=(D2-0.5)/B$1

という式が入っています。その下のセルは、これをコピーしたものが入っています。

この変換式は、「(順位 - 1/2) / 標本サイズ」となっていますが、これでなくてはならないというわけではありません。いくつか提案されている変換式の１つです。

この確率を元に期待値を計算します。

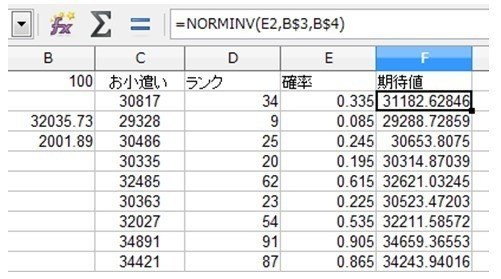
[F2]セルには、

=NORMINV(E2,B$3,B$4) 　　※カッコ内は、「累積確率（ここでは「確率」）」「平均」「標準偏差」

という式が入っています。その下のセルは、これをコピーしたものが入っています。「NORMINV」関数は、平均と標準偏差で表される正規分布関数の累積確率から、それに対応するもとの値を求めます。その値が期待値になります。

次に、NORM.S.INV関数を使って、確率から期待される正規分布を算出します。

例えば、[G2]セルには、

　=NORM.S.INV(E2)

という式が入っています。その下のセルには、これをコピーしていきます。

グラフを描く

そして、「お小遣い」の値をX軸に、「期待値」をY軸に取った散布図を描きます。

・［グラフウィザード］を起動します。
・［グラフの種類の選択］で［散布図］を選択します。

次いで、［データ系列］に進み、[追加]を押します。

・［名前］に「観測値」とつけ、［Ｘ軸］に「お小遣い」のデータ、［Ｙ軸］に「期待される正規分布」のデータを指定します。

さらに［追加］を押し、「期待値」と名前を付けます。

・［Ｘ軸］に「期待値」のデータ、［Ｙ軸］に「期待される正規分布」のデータを指定します。

・［完了］をクリック。

これで散布図が描かれます。ただし、標準ではＸ軸が、Ｙ軸の0の位置に来るので、

・Ｘ軸を選択した状態で右クリックし、メニューから［軸の書式］を選択。
・［位置］のタブを開く。
・［軸線］の［軸交差の位置］で、［始点］を選択して［OK］を押す。

期待値の方のグラフは、マーカーが一直線に並んでいます。これを選択した状態で、右クリックをします。

・［データ系列の書式］を選択。
・［線］タブを開く（標準で開いているはず）。
・［線の属性］で［スタイル］を［実線］、［色］を［灰色５］にする（色は変えてもいい）。
・［アイコン］で［シンボルなし］を選択。

これで、正規分布を表す直線になりました。

実際のデータの分布を示している観測値のマーカーが大きいと思いますが、これは好みの問題なので、適当に調整します。

その他に、

・グラフ全体の縦横比を、1：1に近くなるようにする。
・グラフ全体の右クリック・メニューから［タイトルの挿入］を選択し、グラフ全体の名前を付ける。
・X軸・Y軸でそれぞれ右クリックのメニューから［軸の書式］を選択し、最大値と最小値を指定。
・X軸・Y軸でそれぞれ右クリックのメニューから［軸のタイトルを挿入］を選択し、名前を付ける。
・散布図の点の右クリックのメニューから［データ系列の書式］を選択し、アイコンの大きさや色を調整。
・凡例を削除

などの調整を行ったものが、下の図です。

ちなみに、ＰＳＰＰで描いた正規確率プロットは以下のようになります。