宇宙島へ１６「ラグランジュ・ポイント」

前回の最後で触れた『機動戦士ガンダム』の第一話は、以下のナレーションで始まります。

人類が増えすぎた人口を宇宙に移民させるようになって、既に半世紀が過ぎていた。地球の周りの巨大な人工都市は人類の第二の故郷となり、人々はそこで子を産み、育て、そして死んでいった。

『機動戦士ガンダム』の世界では、人類の多くが宇宙に浮かんだ人工都市スペースコロニーで生活をしています。この冒頭ナレーションの際、画面にはスペースコロニー内の風景が映し出されます。回転する円筒の内壁に作られた都市の様子、太陽光を取り入れるために壁面に設けられた巨大な窓とそこに架けられた橋、窓の向うに見える太陽光反射パネル、そして突如として街を下から打ち破る爆発。

この強烈なイメージによって、日本ではスペースコロニーが一気に一般化しました。

では、まず「スペースコロニー」とは何なのかを考えてみたいと思います。
惑星上にしか人間は住めないという考えを脱却し、宇宙空間に人工環境を建造して住むべきだという主張が出始めたのは20世紀中葉でした。

1929年にイギリスの物理学者ジョン・デスモンド・バナールが『宇宙・肉体・悪魔』の中で、内部が空気が満たされた直径1.6kmの中空の球体で、2万人から3万人が居住するという構想を発表しました。
この構想は現在では「バナール球」と呼ばれています。

「スペースコロニー」は内部に地球上とほぼ同じ環境が再現された人工の宇宙居留地で、その特徴は、おおむね以下のようにまとめることができます。

・重力は1G（加速度が9.8m/s^2）程度である。
・空気の組成が地球と同じであり、気圧・気温・湿度などもほぼ同じである。
・自然な太陽光による24時間で１昼夜の周期がある。
・陸地や海・湖などの水圏を持つ
・地球に準じた生態系がある。

こういった条件を厳密に考えて科学的に提案された構想が、「スタンフォード・トーラス」と呼ばれるドーナツ型スペースコロニーと、「オニール・シリンダー（島３号）」と呼ばれるシリンダー型スペースコロニーです。

『機動戦士ガンダム』のスペースコロニーは基本的に後者の「オニール・シリンダー（島３号）」に基づいていますが、シリーズ中の『機動戦士ガンダムUC』には、宇宙世紀0001に爆破テロで失われた地球連邦首相官邸「ラプラス」という「スタンフォード・トーラス」タイプのスペースコロニーも登場しています。

「スタンフォード・トーラス」は、1975年にスタンフォード大学で開かれたアメリカ航空宇宙局のセミナーにおいて提案されたスペースコロニーのモデルです。直径1.8kmのドーナツ状のトーラスを1分間に1回転することで、遠心力により0.9Gから1.0Gの人工重力を作り出し、日光は、２基の反射鏡によってトーラス内部に取り入れられます。

NASAのエイムズ研究センターが行った「Space Settlement Design Contest 2011」でグランプリを獲得したデザインはこれを拡張したものでした。

また、日本の研究者が提案しているものも、やや奇抜ながらトーラスを用いたモデルです。

しかし、日本で一般にスペースコロニーといえば、どうしてもシリンダー型のイメージが先行しています。

「オニール・シリンダー（島３号）」はアメリカのプリンストン大学教授だった物理学者ジェラード・K・オニールが1976年に『The High Frontier: Human Colonies in Space』の中で提示したモデルで、球形の「島１号」「島２号」というモデルを拡張したものです。
シリンダーのサイズは直径6.5km、長さ33km、自転周期は114秒です。

このモデルでは、スペースコロニーは２基で１セットになっており、互いに逆回転することでジャイロ効果の角運動量（回転する物体はその回転軸を常に一定の方向に向けようとする）を相殺させています。それによって連結したシリンダーを1年間かけて歳差運動（みそすり運動）させながら360度回転させ、回転軸を太陽方向に向き続けることを容易にしています。

さて、「スペースコロニー」の建設場所は、地球・月系の近傍空間では、地球の重力・月の重力・そして「スペースコロニー」が円軌道を周回運動する遠心力、この３つの力が釣り合った力学的な平衡点が有力視されています。

高校の力学では２つの物体が互いに万有引力を及ぼしあいながら運動する「二体問題」はあつかいますが、３つの天体の場合である「三体問題」をとりあつかうことはありません。これは、「二体問題」は一般的に解ける（これを「一般解が存在する」とも言います）のですが、「三体問題」は一般的には解けないことが証明されているからです。

しかしこの場合、地球と月に比べて質量の遥かに小さなスペースコロニーは、質量を無視して計算しても一応は問題がありません。こうした場合の三つの物体の運動を、円運動あるいは楕円運動として考える場合を「制限三体問題」といいます。この場合は問題を解くことができ、その解を「特殊解」と呼びます。

こうして得られた平衡点は月軌道上に２点、月と地球を結ぶ直線状に３点の計５点存在し、それらをフランスの数学者で天文学者のジョセフ・ルイ・ラグランジュにちなんで、「ラグランジュ点(Ｌ1からＬ5）」と呼んでいます。

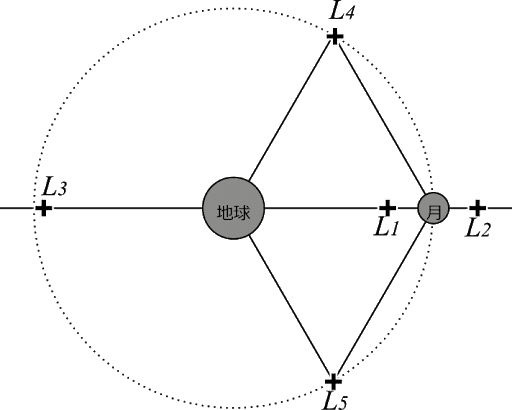
「ラグランジュ点」のうちＬ１からＬ３の３つは1760年ごろにレオンハルト・オイラーが発見した「直線解」とも呼ばれていて、地球と月を結ぶ線上にあります。残りのＬ４とＬ５の２つ点は、1772年にラグランジュが発見した「ラグランジュの正三角形解」と呼ばれていて、地球と月を頂点とする正三角形の頂点の位置にあります。
実際に、太陽・木星で考えると、Ｌ４とＬ５に「トロヤ群」と呼ばれる小惑星群が存在しています。これにちなんでＬ４とＬ５を「トロヤ点」とも言います。

「ラグランジュ点」とは言いますが、実際には太陽やその他の影響もあって、スペースコロニーは「ラグランジュ点」には静止せずに、「ラグランジュ点」を中心にした、ややいびつな「ハロー軌道」とよばれる周回軌道をとります。Ｌ５の軌道全長は約80万kmにもなります。

さて、「ラグランジュ点」のつりあいですが、「直線解」であるＬ１からＬ３については、普通なら地球からこの距離にある小天体が、地球と月を結ぶ直線上に位置したままの角速度で円軌道を周回することはありませんが、小天体に働くのは地球と月の引力の合力であるため、月より外側ではより速く、内側ではより遅く回ることができます。これは感覚的に理解できるでしょう。

ちなみにそれぞれの地球からの距離は、L1=3.26×10の5乗km、L2=4.49×10の5乗km、L3=3.82×10の5乗kmとなります。

問題なのはＬ４とＬ５で、こちらは多少複雑ですが、じっくりと見ていきましょう。
まず最初に注目する点は、複数個の天体を考える場合、その運動は天体系の重心位置を基準点に考えるということです。ここでスペースコロニーなど小天体の質量を無視できるほど小さいと仮定した場合、基準点となる重心点は、地球と月を結んだ線上で、地球と月の質量比:で区切った位置に生まれます。これを中心に円運動をしていると考えます。

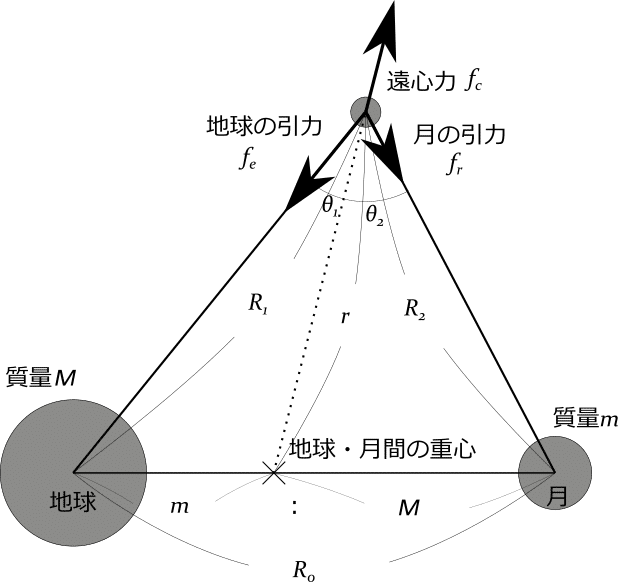
小天体の軌道は、次の二点が満たされれば力の釣り合いが取れているとみなすことができます。

①小天体に働く地球と月の引力の合力が重心点の方向を向いている（遠心力と向きが反対になる）。
②小天体の遠心力が、地球と月の引力の合力の大きさと釣り合う。

よって、３天体の作る三角形が二等辺三角形か正三角形であればよいことになります。

次に②について考えます。

【参考文献】
・廣村達哉、宇佐美元啓、市川朗(2013)「円制限三体問題におけるハロー軌道への移行とその維持」南山大学情報理工学部・数理情報学部2013年度卒業論文要旨集
・伊藤凌平、小出和直、宮沢龍太郎、市川朗(2013)「ラグランジュ点近傍における小ハロー軌道の生成」南山大学情報理工学部・数理情報学部2013年度卒業論文要旨集
・坂東麻衣、大須賀公一、藤井隆雄、山川宏(2012)「円制限三体問題のラグランジュポイントの安定性に関する陰的制御的考察」計測自動制御学会論文集48(7),p431-440
・Carl D. Murray, Stanley F. Dermott(1999)「Solar System Dynamics」Cambridge University Press
・北海道大学 大学院理学院 宇宙理学専攻・惑星宇宙グループ (Planetary and Space Group)「 "Solar System Dynamics" 輪読　section3」2019年4月18参照
・祖父江成尹「ラグランジュ点の位置」2019年4月19参照
・福江純(2002)『ＳＦアニメの科学』光文社
・歌島昌由(1997)『宇宙開発事業団技術報告:ラグランジュ点近傍の軌道力学』宇宙開発事業団
・歌島昌由(2013)「ラグランジュ点軌道(【基礎・応用編】,<連載>えあろすぺーすABC)」日本航空宇宙学会誌 61(1),p35
・NASA Ames Space Settlement Design Contest 2011.Hyperion;Space Settlement
・立川愛弥子,曽我部昌史,石村康生(2013)「スペースコロニー構想 : 長期宇宙滞在を可能にする居住空間の計画」スペース・エンジニアリング・コンファレンス講演論文集21,P.20