宇宙島へ１「ロケットの軌道」

現在、宇宙ビジネスが注目を集めています。

欧州宇宙機関が開発し、「アリアンスペース社」が打ち上げを行っているアリアン・ロケットは世界でもトップクラスの打ち上げ実績を誇り、多くの商業用衛星の打ち上げを行っています。

日本も、HⅡA、HⅡBという大型ロケットに加え、イプシロンという小型ロケットを開発して、商業用の打ち上げに意欲を見せています。国際宇宙ステーションへの補給任務に当たる「こうのとり」や、小惑星からのサンプルリターンに挑んだ「はやぶさ」「はやぶさ２」など、高い技術力は評価されているものの、打ち上げコストの高さ、予算の少なさから、苦戦を強いられています。

一方、世界では純粋な民間企業がこの分野に積極的に参入してきています。

電気自動車メーカー「テスラ」の創業者でCEOのイーロン・マスクが設立した「スペースX」は、民間会社ながら打ち上げロケットの「ファルコン」シリーズと「ドラゴン宇宙船」を開発し、すでに国際宇宙ステーションへの物資供給に参加しています。特に、同社の「ファルコン９」は垂直着陸が可能な、再利用型ロケットとして注目を集めています。

また、2018年1月には、「スペースX」と同じく、アメリカのロケットベンチャー企業「ロケット・ラボ」が、小型ロケットによる商業用衛星の軌道投入に成功しました。

さらに、5月には中国の民間ロケットメーカー「OneSpace Technology」が商業ロケット「OS-X」の打ち上げ実験を成功させ、打ち上げビジネスに参入を果たしています。

宇宙開発の最先端にあるロケットは技術的にも最先端の科学の結晶のように思われがちですが、信頼性の問題から実は実験的な技術はほとんど用いられていません。

しかも、構造は非常に複雑ですが、原理的にはロケット花火やペットボトル・ロケットも基本的には変わりません。

一見垂直に打ち上げられているように見えるロケットですが、実際にはペットボトルロケット同様に斜めに飛んでいます。

ボールを投げると、どこかにすとんと落ちます。
うんと速くなげてやると、ずっと遠くまで飛んでいって、やはり落ちます。
そのボールの速さをどんどん速くしていけば、ずっとずっと遠くへ飛んで行き、ある速度を越えた時点で、永遠に地平線の向こう側へ「落っこち続ける」ことになります。

これが地球をめぐる円軌道運動で、ロケットとは、人工衛星などが「落っこち続ける」ために必要な高さに必要な速度で、推進剤の推力で「放り投げている」のです。垂直に飛ばしては、円軌道に乗せることはできません。

それでは、ロケットの運動について、身近なペットボトル・ロケットを例にとって考えて見ましょう。

ペットボトルロケットは、加圧された空気が推進剤である水を押し出す力を利用して推力Fを得ます。
推力Fは水の噴射速度とノズルの断面積を元に求めることができます。
水の噴射速度Vはベルヌーイの式から、

　すると、推力Fは近似的に以下の式で求めることができます。

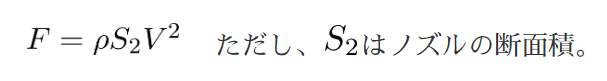
これに対して、反対の方向に空気抵抗Nが働きます。物体に働く空気抵抗は、空気の流れに対する断面積と大気密度、それから速度の２乗に比例します。 そのとき、抵抗係数を比例定数として用います。
空気抵抗Nは次のように求めることができます。

普通、ペットボトルロケットは傾けて飛ばしますから、推力Fは水平方向(Ｘ軸)と垂直方向(Ｙ軸)に分解して考えることができ、垂直方向の推力Fyと反対向きに重力Gがかかります。
よって、水噴射時にロケットに働く力は以下のようになります。

水の質量と水噴出時間は、以下の式で簡易的に求めることができます。

実際には、水の量が変化すると空気の体積が増えて圧力が下がるため、噴射速度も遅くなってしまいますので、詳細な計算が必要になります。

水の噴射が止まった場合、ペットボトルロケットは慣性飛行に入ります。すると、推力Fは働いていませんので、空気抵抗と重力だけが働きます。つまり、F=0なのでロケットに働く力は以下のようになります。

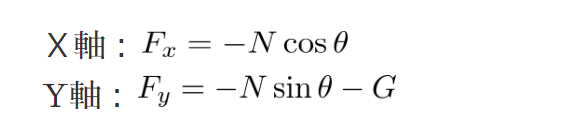
ここで、ロケット本体の質量をもとに、ロケットのX軸方向の加速度とY軸方向の加速度が、運動方程式F=maから以下の式で求めることができます。

ロケットの速さのX軸成分とY軸成分はそれぞれ、時間との関係で次のように求めることができます。

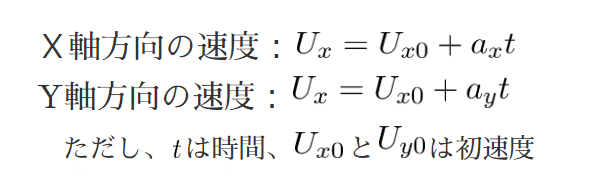
ただし、初速度は0ですから、この場合なくても同じです。

速度が分かれば、ある時点におけるロケットのX軸、Y軸の位置を計算することが可能となります。
なお、ロケットの速さは「三平方の定理（ピタゴラスの定理）」から、

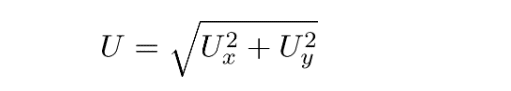
となります。もちろん、推力を用いて、運動方程式から加速度を

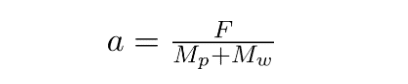
と求めてから、

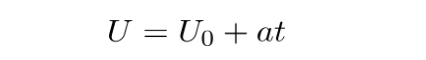
としても求めることができます。

実際には、時間と共に水が噴出して質量が変化し、それによって加速度も変化するため、軌道を計算するには、今までに説明した式だけではなく、若干の工夫が必要です。

試みに、水の噴出に伴う圧力の変化と、水がなくなった後の空気の噴射を考慮しない簡易的な形で、表計算ソフトを使って軌道を計算してみます。
入力パラメータは、以下の通りです。

・ロケットの自重（初期値は0.08kg）
・水の量（初期値は0.2kg）
・ペットボトル断面半径（初期値は0.05m）
・ノズル半径（初期値は0.003m）
・ボトル内圧力（初期値は３気圧）
・外気圧（通常は１気圧）
・発射角度（初期値は45°。rad(ラジアン)に変換して用いる）
・ガイドレールの長さ（初期値は0.1m）
・空気抵抗係数（初期値は0.34。半球または頂角30°の円錐の値）
・時間のステップ（初期値は0.04秒）

※1radは、円周上で半径rと同じ長さの弧lを描く角度にあたりますから、円一周はradとなります。

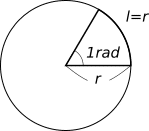
数値を順次計算していけば、軌道をプロットすることができます。
この初期値の場合、最大到達高度は約7m、最大到達距離は約32mとなります。

表計算ファイルは、エクセルとOpenDocument スプレッドシートを用意していますので、ダウンロードしてご利用ください。

ようするに、本物のロケットもこの規模の大きいものと言うわけです。

【参考】
・AUTOSPORTweb(2018)「テスラの最速電気自動車が宇宙を“ドライブ”。米宇宙ベンチャーがロケット打ち上げ」AUTOSPORTweb 2018年2月7日
・石田真康(2018)「小型ロケットでRocket Labが快挙　商業化加速」ITmedia ビジネスオンライン 2018年1月27日
・Sputnik「中国で初の商業ロケットの実験に成功」Sputnik 2018年05月17日
・nozomu Home Page-「ペットボトルロケットの軌道計算」