[PSPP]回帰分析③

ロジスティック回帰分析

目的変数が「あり/なし」のような二値の変数の場合に用いられるのがロジステッィク回帰分析です。

「あり/なし」を「1/0」とした場合、右図のように通常の回帰分析で直線を当てはめると、予測値が1と0の間には収まらなくなってしまいます。そこで最小値が0、最大値が1となるようなロジスティック曲線と呼ばれるＳ字曲線にあてはめて予測・説明を行うのがロジスティック回帰分析です。

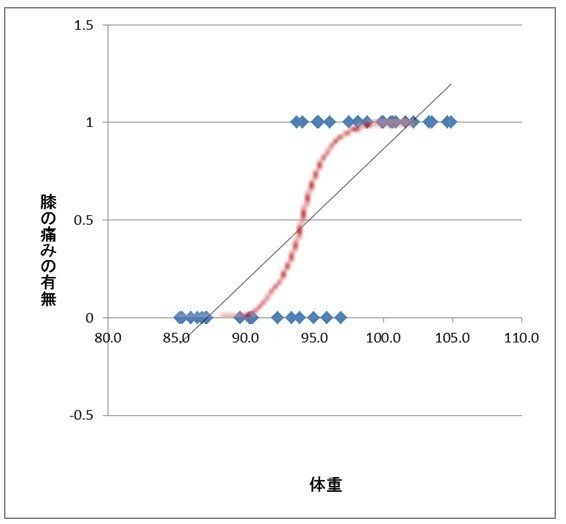
目的変数が２値であるので、その事象が発生する確率を直接予測することになります。

ロジスティック回帰分析の回帰式は次のとおりです。

ロジスティック回帰分析では、回帰係数bを用いて計算されたオッズ比exp(b1)が算出されます。説明変数X1が１だけ増加した場合に、exp(b1)倍に増えることになります。たとえば、「年齢が1歳増えたら高血圧のリスクが1.075倍になる」のように言うことができます。

ロジスティック回帰分析の実行

ここでは，上で図示した体重と膝の痛みの有無のデータを使い、体重によって膝の痛みの有無を説明するロジスティック単回帰分析を実行してみましょう。

・[分析]-[回帰]-[２項ロジスティック回帰]を選択する。

・従属変数（目的変数）に「膝の痛み」を指定。
・独立変数（説明変数）に「体重」を指定。（SPSSでは共変量）。

・[オプション]ウインドウを開き、［CI for exp(B)］にチェック。

このとき、特に意図がなければ「％」の設定は「95」のままで大丈夫です。これによって、結果にオッズ比（exp(bk)）の95％信頼区間が算出されます。（ＳＰＳＳでは、[Hosmer-Lemeshowの適合度]と［Exp(b)の信頼区間］にチェックを入れておく）。

出力の見方

ここでは、主要な部分のみを解説します。

まず「ケース処理の要約」の表を見ます。

この表には、分析したケース数が表示されています。変数中に一つでも欠損値があれば、そのケースは分析から省かれるので、分析に実際に用いられたケース数をここで確認します。この場合は、40件100％であるので、すべてのケースが処理されています。

「分類表（分類テーブル）」では「全体のパーセント」を確認します。これは大雑把に言うと、的中率に相当します。この場合は87.5％あるので、87.5％くらいはこのモデルで当たるというようなことですから、モデルに適合していると言えそうです。

　最も重要なのが、「等式内の変数群（方程式中の変数）」の表です。

　「B」が回帰係数b（対数オッズ比）、「Exp(B)」がオッズ比を示しています。一番左はオッズ比の95%信頼区間です。なお、切片を意味する定数が表の一番下に来ている点が重回帰分析の表と異なるので、注意が必要です。

　ここでは、「B」が.78、「Exp(B)」が2.17、「有意水準」が.007ですから、「体重」は係数として意味があると判断でき、「体重が1kg増えると、膝の痛みを持つ確率が2.17倍になる」と言えます。

　この場合、回帰式は、

となり、たとえば体重90kgの場合、膝の痛みを持つ確率は2.99％ですが、体重95kgの場合は60.35%にまで高くなることが計算できます。

　最後に、「モデル集計」を確認します。

この表には、-2×対数尤度、擬似決定係数である「コックス・スネルのR２乗（Cox-Snell R2乗）」「ナゲルケルケの＋Nagelkerke R2乗」などが出力されるので確認する。