宇宙島へ３「宇宙速度」

ロケットを宇宙まで打ち上げるにはどうすればいいのかは、前回まであらましをつかむことができました。
それでは、一体どのくらいの速度が必要になるのかを、詳細に考えて見ましょう。

まずはおさらいです。

ボールを水平に投げると、どこかにすとんと落ちます。うんと速くなげてやると、ずっと遠くまで飛んでいって、やはり落ちます。そのボールの速さをどんどん速くしていけば、ずっとずっと遠くへ飛んで行き、ある速度を越えた時点で、永遠に地平線の向こう側へ落っこち続けることになります。

第１宇宙速度

これが地球をめぐる円軌道運動です。
この円軌道運動にのる速度は「第１宇宙速度」とも呼ばれ、地球の場合は以下の式で表されます。

一般的には、μの代わりに、重力定数Gに天体の質量Mをかけたもので表されます。
すると、赤道上の地表での「第１宇宙速度」は、地球の赤道半径が約6378kmなので、およそ秒速7.9kmとなります。

しかし、実際に人工衛星が回っているのは、赤道上の地表すれすれなどではありません。赤道の遥か上空の静止衛星軌道上です。

静止衛星軌道上では、24時間（正確には23時間56分4秒です）で地球の周りを1周することができます。

では、その高度を求めてみましょう。

ここで、単位時間当たりの角度の変化を表す角速度ωを導入します。角速度のにおける角度の変化にはrad（ラジアン）を用います。

これは、ペットボトルロケットの軌道計算のところでも使用しています。軌道上の速度は角速度ωで表すことができるので、次のように求めることができます。

静止衛星軌道上での角速度は、24時間で１周なので「2πr/24時間」と考えることが出来ます。これを上の式に代入すると、

となります。これを半径rについて解くと、

となり、 約4万2300kmとなります（23時間56分4秒を用いて計算すると約4万2200km）。これは地球の重心からの距離なので、赤道半径を引くと、約3万5900kmとなります。

このときの第一宇宙速度は、

と、秒速約3.07kmとなります。
高度が大きい方が速度が遅くなるのは、地球の重心から離れれば離れた分だけ、地球の引力が小さくなるからです。

第２宇宙速度

「第２宇宙速度」とはなにかというと、地球の引力を脱するための速度です。以下のように表されます。

静止衛星軌道を飛び出して、他の惑星に探査機を送り出そうとすると、最低でもこの「第２宇宙速度」を出す必要があります。
この速度を先ほどと同じ赤道上の地表すれすれで計算すると秒速約11.2kmとなります。つまり、赤道上の地表から接線方向（水平）にこの速度でボールを打ち出せば、地球の引力を振り切って飛んでいく（理論的には）ということです。
しかし、この場合でも、もっと大きな太陽の引力には捕らえられることになります。つまり、いずれは太陽の引力につかまって、太陽の周りを回る軌道に乗ることになります。

第３宇宙速度

それでは、太陽の引力を脱して太陽系を飛び出すのに必要な速度はどうやって求めればいいのでしょうか。基本的には「第２宇宙速度」の式と同じで、地球であった部分を太陽に置き換えればよく、

となります。これを「第３宇宙速度」といいます。
日心重力定数は、重力定数Gに太陽の質量をかけたものです。
地球の軌道上から発射して太陽系を離脱する「第３宇宙速度」を計算すると、およそ秒速42.1kmとなります。

ただし、これは太陽から見た速さなので、地球からの場合、地球が公転運動している分の速度を差し引かなければいけません。

地球の公転速度は、地球の公転による遠心力と太陽地球間の引力が釣り合うという関係から、

と求めることができます。したがって地球公転軌道からの脱出速度は、

となります。なお、公転速度と「第３宇宙速度」との関係は、「第１宇宙速度」と「第２宇宙速度」の関係と同じで、

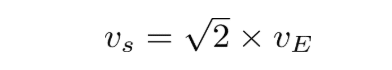
が成り立ちます。

第４宇宙速度以上

通常使用されるのはこの「第３宇宙速度」までですが、近年は「第４宇宙速度」以上も提唱されています。

「第４宇宙速度」は銀河系脱出速度です。
基本的には「第２宇宙速度」「第３宇宙速度」の式と同じで、銀河系の質量と、銀河の重心からの距離を用います。
つまり、脱出速度は以下のように一般化できます。

ある主天体からの脱出速度は、主天体の質量とその主天体からの距離、そして重力定数を使って、

で表すことができ、主天体から距離Rにある周回軌道上の天体rから見た場合は、その天体の周回速度

を差し引くので、天体rから見た主天体からの脱出速度は、

となります。また、

が成り立ちます。つまり、天体rから見た主天体からの脱出速度、天体rの周回速度を用いて、

と表現することができます。

それでは、「第４宇宙速度」を求めてみることにしましょう。

銀河系の中心から太陽までの距離は、約2.8万光年です。一方、銀河系の質量は諸説ありますが、ここでは太陽質量1.99×10の30乗kgの2.0×10の12乗倍として計算してみます。
すると、銀河系から見て秒速約450km/s、太陽から見て秒速約130kmとなります。
「第４宇宙速度」は、アルメニアの天文学者Grigor A. Gurzadyanの「Theory of Interplanetary Flights」(1996,CRC Press)にも記されているので、一応研究はされているようですが、「第５宇宙速度」以上は、ＳＦの世界以外の何者でもありません。

「第５宇宙速度」は銀河集団からの脱出速度です。ここまでくると計算の元となる数値がかなり曖昧になってくるので、秒速約1000～2250km/sくらいではないかとされています。

「第６宇宙速度」は宇宙からの脱出速度です。宇宙は高速で膨張しているとされていますから、光速度約30万km/s以上が必要となります。

【参考】
・石原藤夫・金子隆一(2009)「軌道エレベーター　宇宙へ架ける橋」早川NF文庫
・福江純「ロンギヌスの槍－第n宇宙速度－」
・krzysztof Mastyna(2013)The cosmic velocities.
于鳳軍(2017)「月球上的“第四”宇宙速度」大学物理36(2),pp.8-10