
マルチレベルモデルの基礎(+セミナー体験)
1.初めに
初めまして!
株式会社GA technologies、Advanced Innovation Strategy Center(AISC)の宋です。
現在、Data Science部門内において働いています。
今回は、2022年11月から新設されたエンジニア向け福利厚生である「テックチャージ」(自己研鑽制度)を利用してRで学ぶマルチレベルモデル入門のセミナーに参加したので体験談をお届けします!また、記事の後半ではセミナーの振り返りを兼ねてマルチレベルの解説も行っているので併せてご覧ください。これを読めばマルチレベルモデルの基礎と全体像が理解できるはずです。
GA technologiesのテックチャージ(自己研鑽制度)を使って今回のセミナーに参加しました!前は年3万円の制限がありましたが、今は利用回数や金額の制限なく使うことができます!GA technologiesとAISCに興味を持ってくださった方はこちらとこちらをご確認ください!
2.当日の様子
講師は、筑波大学大学院人文社会ビジネス科学学術院ビジネス科学研究群経営学学位プログラムの尾崎幸謙准教授です。研究領域は統計科学(構造方程式モデリング、テスト理論、マルチレベルモデル)、行動遺伝学、社会調査です。
オンラインセミナーのため、当日は業務時間で会社のパソコンを使って会社のウェブ会議の参加をするためのスペースの中で視聴しました。
3.マルチレベルモデルの基礎と全体像
セミナーでマルチレベルモデルを勉強しましたので、ここで自分が学んだことをアウトプットします。
3-①基礎
マルチレベル分析(Multi-Level Analysis)とは、階層的な構造を持ったデータを分析するための手法です。
階層的な構造を持ったデータは、単一のレベル(例えば、個人レベル)だけでなく、複数のレベル(例えば、ペア・グループ・縦断レベル)を含みます。
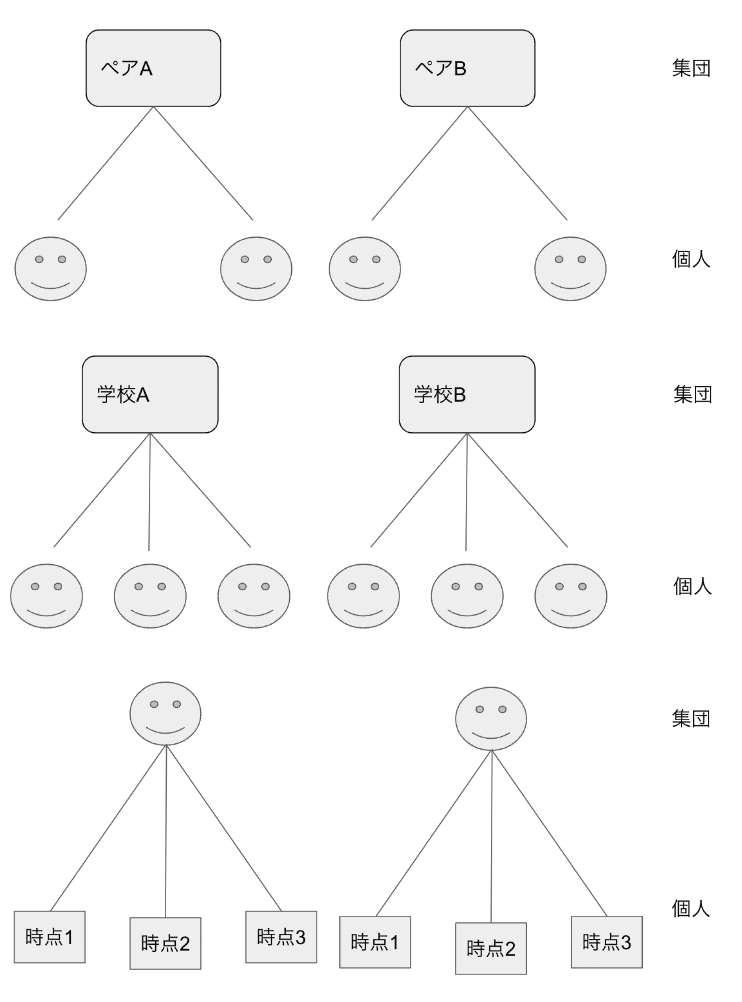
複数の集団から個人レベルと集団レベルのデータを収集し、各集団で個人レベルの変数の平均や相関が異なる場合にマルチレベル分析が使われます。
もし、データの階層性を無視して普通の分析手法で分析すると、誤った結果を導く恐れがあります。
例えば、各学校から同数の生徒を無作為に抽出し、勉強時間とテスト点数の関係を調査したと仮定します。 しかし、勉強時間とテスト点数との回帰分析の結果だけでは、勉強時間がテスト点数向上に有効であることはわからないです。

なぜなら、生徒のテスト結果は、生徒個人の努力に加え、生徒が所属している集団にも影響されるからです。 同じ学校に通っている学生たちは、同じレベルの先生のもとで同じ教育方法で勉強しているなど、学習状況が結構似ています。そのため、集団内で相関関係が高くなります。仮に個人の勉強時間とテスト点数の回帰分析を行った場合、個人の努力と集団の影響の両方が混在した結果になるでしょう。だから、ここでは簡単に個人の努力がテスト点数に寄与していると結論づけることはできないでしょう。
こういうデータに対しては簡単な回帰分析ではなく、マルチレベルモデルを使うべきです。
3-②分析の全体像
マルチレベル分析の大まかな流れとしては、以下のようなものです。
データの階層性を評価すること
級内相関係数を算出すること
データに対して個人レベルと集団レベルの変数を用意すること
個人レベルの変数は集団平均中心化を行う
集団レベルの変数は全体平均中心化を行う
モデリングして推定値を出すこと
それぞれのマルチレベルモデルを適用してモデルの結果に対して解釈。
各モデルのAICとBICを出して最適なモデルを選ぶ。
マルチレベルモデルの分析にはR言語の「lmertest」というパッケージを使用しています。lmertestでデータに対して目的に合わせたモデルを適切に書いていけば、知りたい値の推定値を出力してくれますので、階層構造を持つデータに対する分析が容易になります。
もし分析の全体像でちょっと物足りないと感じているなら、別の記事として用意しています。各モデルの数式と説明は付録に書いています。付録に各過程について簡単に説明します。
1:データの階層性を評価すること
最初はデータの階層性を評価します。それは級内相関係数を計算することです。級内相関係数とは目的変数の分散のうち,集団間の分散で説明される割合です。
Rの「ICC」パッケージを使えば、「data」を読み込んで、以下のコードを実行すれば以下のように簡単に計算できます。
library(ICC)
ICCest(as.factor(集団を表す変数), 目的変数, data=data, alpha=0.05, CI.type=("Smith"))マルチレベル分析を適用すべきかどうかを判断できる指標としてはわかりやすいです。明確な基準はありませんが、級内相関係数は有意で、0.1以上あれば、このデータはマルチレベルモデルを適用したほうがいいと言われています。
またこの記事では級内相関係数の具体的な計算方法までは求めていないので、具体的な計算方法などはわからなくても大丈夫です。具体的な数式に対して興味があれば付録を参照してください。
2:データに対して個人レベルと集団レベルの変数を用意すること
本番のモデリングに入る前に、まず個人レベルと集団レベルの変数を用意します。実際のモデリングの際に必要となります。この手順は説明変数の中心化と言います。例えば学校の例で言うと、勉強時間が説明変数で、テストの点数が目的変数になっています。個人レベルの変数はa.集団平均中心化を、集団レベルの変数ではb.全体平均中心化を行います。これからはa.集団平均中心化とb.全体平均中心化を説明します。
一つ目はa.集団平均中心化(Centering Within Cluster:CWC)です。

CWC 後の説明変数は個人の集団内での相対的な値の高さを表して、集団レベルの影響を除外したので、 CWCを行った説明変数は個人レベル効果になります。
もう一つはb.全体平均中心化(Centerring at the grand mean:CGM)があります。
個人レベルで全体平均中心化をしたら、CGM後の説明変数は個人の全体内での相対的な値の高さを表しています。個人レベルと集団レベル両方の影響を含んでいます。でも個人レベルで全体平均中心化するのは後のモデリングではあまり使われていないです。
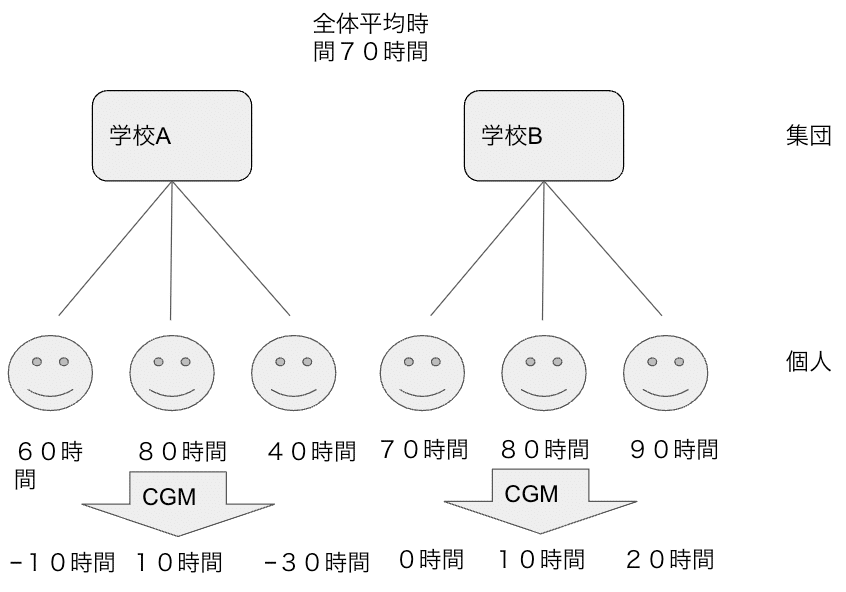
集団レベルで全体平均中心化したら、集団平均−全体平均になり、集団が全体での相対的位置を表します。この時の説明変数は集団レベル効果になります。集団レベル効果を知りたい場合では集団レベルで全体平均中心化するのは必須です。

3:モデリングして推定値を出すこと
マルチレベルモデルはランダム切片モデルとランダム傾きモデルに分かれています。
ここでのランダムの意味は、集団によって異なることです。つまり、ランダム切片モデルは以下の図のように、切片だけが集団ごとに異なることです。
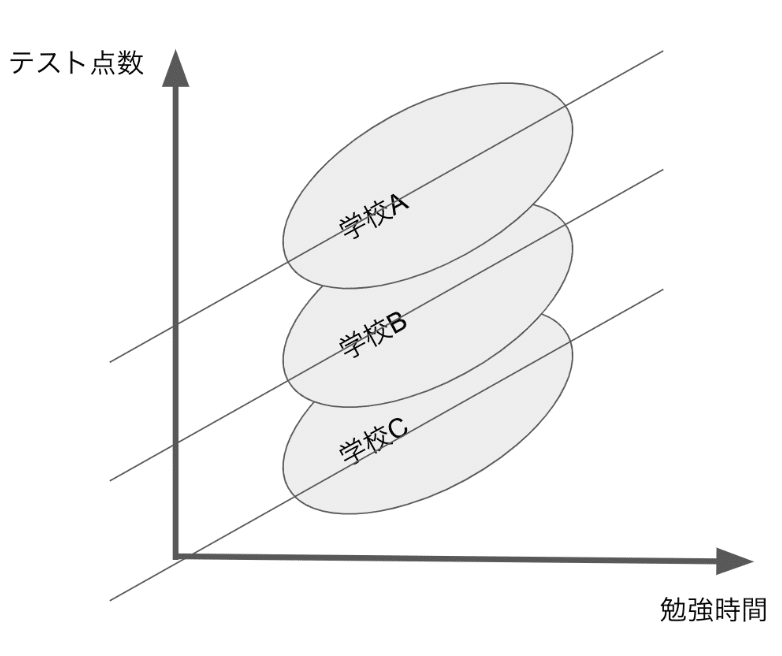
ランダム傾きモデルは下図みたいに、切片だけでなく、傾きまで集団ごとに異なることです。

下のテーブルはそれぞれのマルチレベルモデルと各分析目的です。分析目的に合わせてモデルを選定します。

RのlmerTestパッケージを使うなら、各モデルのコードを適切に書いていけば、簡単に推定したいパラメータを推定できます。各モデルのパラメータと詳しい数式の説明は付録で書いています。
そして各モデルとデータの適合度を計算して比較し、一番適合度が高いモデルを選択します。推定の際にAICとBICという情報量規準も一緒に出力されます。
最後に選定したモデルの結果に対して分析の目的と合わせて考察をすれば、マルチレベル分析の大まかな流れは終わりになります。
4.セミナーの感想
3で話した内容はあくまで概要で、セミナーではもっと詳しい内容、例えば発展的なモデルとマルチレベルモデルの過去の研究事例もたくさん紹介されていました。
会場には行けなくて雰囲気を体験できなかったですが、質疑タイムがあって質問もできて、講師のスライドや映像を見ながら進めることができましたので、効率的だったかもしれません。開催された時間が業務時間中だったため、会社のウェブ会議の参加をするためのスペースでセミナーを受講しました。ややスペースが狭いですが集中できる環境ですね。
そしてセミナーの内容については、『Rで学ぶマルチレベルモデル入門編』と『Rで学ぶマルチレベルモデル実践編』の内容に沿って、マルチレベルモデルの適用する場面や、各種マルチレベルモデルのエッセンス、Rを使った実践的な解析方法、やや発展的なモデルを一通り先生に講義してもらいました。
セミナーのおかげで、マルチレベルモデルが適用できる場面やその理由がより明確になりました。また、様々なマルチレベルモデルについても、分かりやすく説明していただいたので、理解が深まりました。
理論以外にも実践の機会もありました。基本的なマルチレベルモデルのRコードとデータをもらって実行し、その結果から解釈する方法を先生が詳しく説明して下さりました。実際に手を動かして解析することで、よりモデルへの理解が深まったと感じます。
一日だけではこんな分厚い内容を全部消化するのは非常に難しいです。だから聞いた後にもう終わりではなくて、資料を何度も繰り返して読んで理解することも必要です。そこで、自分が学んだことを再整理するためにこの記事でマルチレベル分析の振り返りを行いました。今後も実務や研究でマルチレベルモデルを適用する機会があれば、Rを使って解析し、適切な解釈をすることができるようになったら嬉しいです。
セミナーの延長として、現在私が取り組んでいる研究にマルチレベルモデルをどのように適用できるかについても検討しました。
不動産業界でマルチレベルモデルを使った論文があるかどうかを調べたら、山形 (2011) は戸別マンションデータにヘドニック分析を適用して、不動産の環境性能と災害リスク指標のマンション価格への影響について分析を行いました。今後もし私がマンションのブランド性と地域性について研究する時も参考にできるかもしれません。
5.参考文献
山形与志樹, 村上大輔, 瀬谷創, 堤盛人: 環境・災害 リスク指標とマンション価格のマルチレベルモデルによる空間計量経済分析, 土木計画学研究・講演集, 43, 2010.
尾崎 幸謙・川端 一光・山田 剛史 (2018) 『Rで学ぶ マルチレベルモデル[入門編]』.朝倉書店.
尾崎 幸謙・川端 一光・山田 剛史 (2019) 『Rで学ぶ マルチレベルモデル[実践編]』.朝倉書店.
6.付録
各モデルの数式、説明、分析の詳しい過程は下のリンクに書いています。
