【ラビットチャレンジ】ステージ2/機械学習レポート

・線形回帰モデル

直線と曲線の2種類で表現し、説明変数から目的変数を出力する。

予測値には＾を付ける。ｘを入力してｙ＾を出力する。

いろいろな線形の組み合わせの表現

【目的】：

説明変数とパラメータを掛けたものが予測結果となるのでその予測と、未知の問題の答えをズレなく答えたい。

【手段】：

●ズレの確認：今有る教師あり学習データを検証用と学習用に切り分け学習させる。学習方法は最小平均二乗法や最小二乗法等。

●学習用と予測結果を比べる。ズレた分を元にパラメータｗを調整したい。ズレが小さくなるようなパラメータを考える。

●最小二乗法の場合一意にて出力できる。（最尤法でも同じ値が出力出来る）

モデルの考え方/手段：

●単回帰

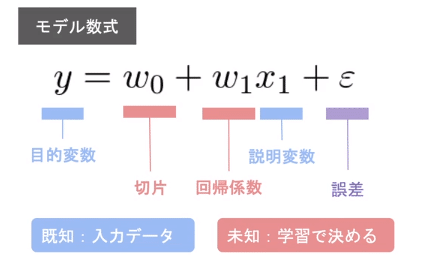
与えられた説明変数と目的変数の関係は上記のように考える。見えない切片と回帰係数と誤差が存在すると考える。

●重回帰

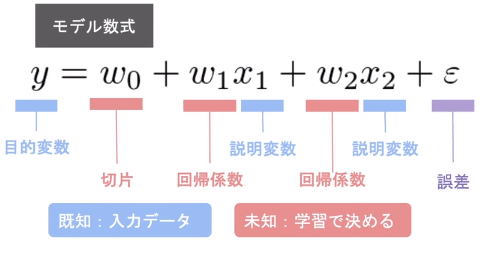
1個以上のｍの場合は重回帰と呼ぶ。曲面になる。

モデルに使うデータの使い方/手段：

ホールドアウトとK分割交差検証がある。

最小平均二乗法でｗの最小を求める/手段：

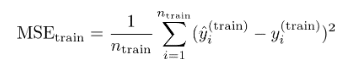
式を微分することで傾きを求める事を考え傾きが「0」が最小と考える。しかし、縦の一番最小を求めるのではなく、その時の横を求めたい。

実数のｍ+1の中の一つのｗの高さが最小の時の、横を知りたい（ａｒｇ）という意味。

式の変換で一意に見つかるか確認/手段

実装短回帰分析/手段：

from sklearn.datasets import load_boston
from pandas import DataFrame
import numpy as np

# ボストンデータを"boston"というインスタンスにインポート
boston = load_boston()​

type(boston)​

>>sklearn.utils.Bunch

Bunchと言うタイプとの事。

Bunchをprintすると。

print(boston)

中身、、、省略し重要な文面は

['　':]ごとの文章「data / target / feature_names / DESCR」の記載。

data=説明変数、target= 目的変数、feature_names=カラム名、DESCR=カラムの簡単な説明。

データフレームとして取り込み方、データとカラムを指定。説明変数。

#　説明変数らをDataFrameへ変換
df = DataFrame(data=boston.data, columns = boston.feature_names)

目的変数は

# 目的変数をDataFrameへ追加
df['PRICE'] = np.array(boston.target)

PRICEカラムを作成し、dfに入れる。

# 最初の5行を表示
df.head(5)

目的変数まで含まれたデータフレームが完成。

data = df.loc[:, ['RM']].values
target = df.loc[:, 'PRICE'].values

from sklearn.linear_model import LinearRegression
model = LinearRegression()

model.fit(data, target)

部屋数と金額を取り出して、model = LinearRegression() 学習、fit学習させて、パラメータ完成。

df["RM"].min()

結果：部屋数は最低3.5なので１部屋や2部屋は正しく予測できない。

実装重回帰分析/手段：

説明変数を2つ以上使用する。

# 説明変数
data2 = df.loc[:, ['CRIM', 'RM']].values
# 目的変数
target2 = df.loc[:, 'PRICE'].values

model2 = LinearRegression()
model2.fit(data2, target2)

2つ引数を使用して出力するパラメータが作成。

model2.predict([[0.0, 7]])

犯罪が0でも0.2でも金額はほどんど変わらない様子

print(model.coef_)
print(model.intercept_)

print(model2.coef_)
print(model2.intercept_)

[9.10210898]=モデル1パラメータ
-34.67062077643857＝モデル1切片
[-0.26491325 8.39106825]＝モデル2パラメータ
-29.24471945192992＝モデル2切片

結果：これを確認すると、犯罪率の1の変化が部屋の価格0.3程度しか確かに作用しない。

・非線形回帰モデル

【目的】：

説明変数とパラメータを掛けたものが予測結果となるが、結果が非線形である場合のモデルの考え方と、説明変数を増やした時のオーバーフィットの抑制を考える。

【手段】：

非線形の表現の一つとしてXiをX^3などの関数に変えてその非線形関数をΦ（ｘ）と考える。ｗは線形のままでパラメータ調整を考える。

　表現/手段：

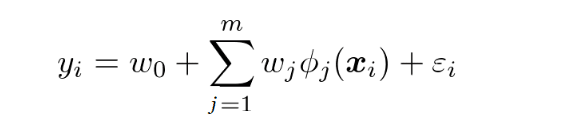
Φ（X）を基底関数という。

基底関数も線形回帰と同じように推定することが出来る。

なので自由度の高い測定ができそう。

なので多様な関数を増やせば、曲線で表現出来て精度の高い予測が可能になるのではないかと考えるが、その場合のオーバーフィット過学習を抑制するために出来ること/手段：

●表現力を減らす。不要な基底関数削除

●正則化法

パラメータｗが大きくならないようにする。

※KernelRidge回帰はalphaとgammaという2つのハイパーパラメータ―がある。alphaは正則化(過学習しないよう抑える働き)の強度、gammaは適用する関数の形を決めるパラメーター。

※kernel='rbf'　は　曲線の関数

from sklearn.kernel_ridge import KernelRidge

clf = KernelRidge(alpha=0.0002, kernel='rbf')
clf.fit(data, target)

p_kridge = clf.predict(data)

plt.scatter(data, target, color='blue', label='data')

plt.plot(data, p_kridge, color='orange', linestyle='-', linewidth=3, markersize=6, label='kernel ridge')
plt.legend()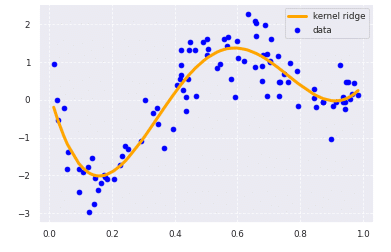

ちなみに、表現力の抑制を行わない状態のパラメータ

clf = KernelRidge(alpha=0, kernel='rbf')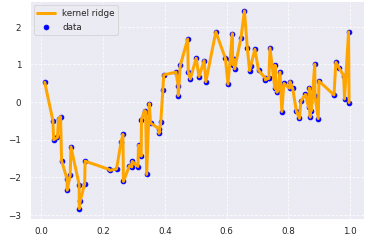

deg = [1,2,3,4,5,6,7,8,9,10]
for d in deg:
   regr = Pipeline([
       ('poly', PolynomialFeatures(degree=d)),
       ('linear', LinearRegression())
   ])
   regr.fit(data, target)
   # make predictions
   p_poly = regr.predict(data)
   # plot regression result
   plt.scatter(data, target, label='data')
   plt.plot(data, p_poly, label='polynomial of degree %d' % (d))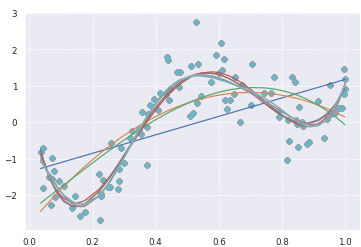

4以上はほどんど重なりが有るので不要と判断も可能。

from sklearn import model_selection, preprocessing, linear_model, svm

# SVR-rbf
clf_svr = svm.SVR(kernel='rbf', C=1e3, gamma=0.1, epsilon=0.1)
clf_svr.fit(data, target)
y_rbf = clf_svr.fit(data, target).predict(data)

# plot

plt.scatter(data, target, color='darkorange', label='data')
plt.plot(data, y_rbf, color='red', label='Support Vector Regression (RBF)')
plt.legend()
plt.show()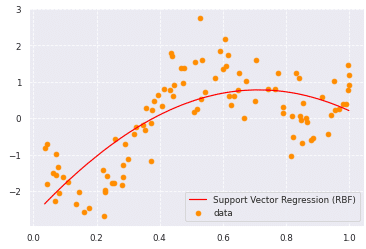

from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(data, target, test_size=0.1, random_state=0)
from keras.callbacks import EarlyStopping, TensorBoard, ModelCheckpoint

cb_cp = ModelCheckpoint('out/●●●.{epoch:02d}-{val_loss:.2f}.hdf5', verbose=1, save_weights_only=True)
cb_tf  = TensorBoard(log_dir='out/●●●', histogram_freq=0)

def relu_reg_model():
   model = Sequential()
   model.add(Dense(10, input_dim=1, activation='relu'))
   model.add(Dense(1000, activation='relu'))
   model.add(Dense(1000, activation='relu'))
   model.add(Dense(1000, activation='relu'))
   model.add(Dense(1000, activation='relu'))
   model.add(Dense(1000, activation='relu'))
   model.add(Dense(1000, activation='relu'))
   model.add(Dense(1000, activation='relu'))
   model.add(Dense(1000, activation='linear'))
   model.add(Dense(1))

   model.compile(loss='mean_squared_error', optimizer='adam')
   return model

from keras.models import Sequential
from keras.layers import Input, Dense, Dropout, BatchNormalization
from keras.wrappers.scikit_learn import KerasRegressor

estimator = KerasRegressor(build_fn=relu_reg_model, epochs=100, batch_size=5, verbose=1)
history = estimator.fit(x_train, y_train, callbacks=[cb_cp, cb_tf], validation_data=(x_test, y_test))

・ロジスティック回帰モデル

扱う問題は、分類問題。

教師データのある、説明変数。

線形回帰を関数を挟んで1から0の値に変換する。

【目的】：

尤度関数の微分を行うために（ｗのパラメータの為に）、シグモイド関数の微分を行う。

【手段】：

【目的】：

目的のｗを探す

【手段】：

最尤法を使用する。

尤度関数を最大化する。今回ベルヌーイ分布から最もらしいｗを考えるとする。

ベルヌーイは↓

複数の場合が↑となる。

未知の確率Pを知りたいが本当に知りたいのはそれを構成するｗを知る必要がある。Pはシグモイト関数を通したｗがある。

この最大のｗを探す。

このことからｗを微分出来ることが分かる。

ｗで微分する/手段：

ｌｏｇは桁落ちしないため。

ｗは解析的に求められないので勾配法にて探索する。

勾配法には確率降下法などが有る。

【結果】

判断方法：

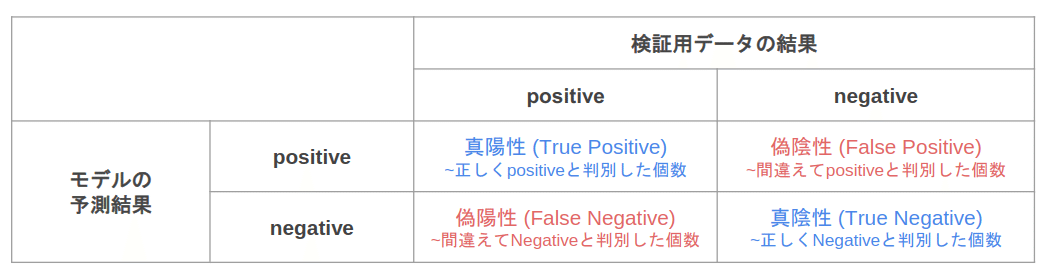
上記をもとに判断の方法が有る。

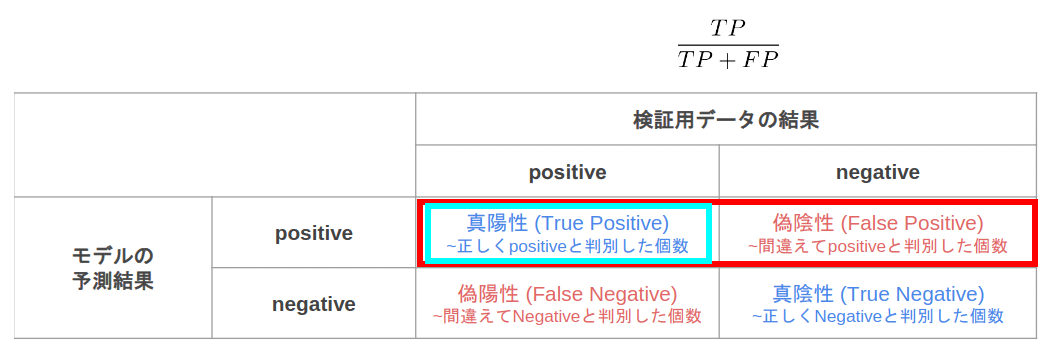
どの判断の仕方がいいと言うわけではなく、立場により判断の仕方が違う。

例：医者が患者に病気と診断した場合

医者だった場合、実際陽性な人の中で正しく陽性と判断できたか。が重要だし、患者の場合は予測された陽性と診断された中で本当に陽性なのかが気になるため、立場の違いによる判断材料としてそれぞれ使用される。

ロジスティック回帰/ハンズオン

【目的】：

titanicデータセットを利用し分類してみる。

【手段】：

ロジスティック回帰を使用する。

from google.colab import drive
drive.mount('/content/drive')

googleドライブマウント

モジュールのインポート。

#from モジュール名 import クラス名（もしくは関数名や変数名）
import pandas as pd
from pandas import DataFrame
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
#matplotlibをinlineで表示するためのおまじない (plt.show()しなくていい)
%matplotlib inline

# titanic data csvファイルの読み込み
titanic_df = pd.read_csv('/content/drive/My Drive/study_ai_ml/data/titanic_train.csv')

#予測に不要と考えるからうをドロップ
titanic_df.drop(['PassengerId', 'Name', 'Ticket', 'Cabin'], axis=1, inplace=True)

#nullを含んでいる行を表示
titanic_df[titanic_df.isnull().any(1)].head()

titanic_df['AgeFill'] = titanic_df['Age'].fillna(titanic_df['Age'].mean())
#再度nullを含んでいる行を表示 (Ageのnullは補完されている)
titanic_df[titanic_df.isnull().any(1)]

titanic_df.isnull().sum()

nullの部分の確認

data1 = titanic_df.loc[:, ["Fare"]].values
label1 =  titanic_df.loc[:,["Survived"]].values

from sklearn.linear_model import LogisticRegression
model=LogisticRegression()
model.fit(data1, label1)​

print(model.predict_proba([[61]]))
print(model.predict([[61]]))
print(model.predict_proba([[62]]))
print(model.predict([[62]]))

【結果】：

この場合分類されたものをどれくらいの確率で判断されているのか確認する事も可能。そして、この場合、金額が62以上が50％を超える境界線だと分かる。

【補足】：

グラフ化

w_0 = model.intercept_[0]
w_1 = model.coef_[0,0]


def sigmoid(x):
   return 1 / (1+np.exp(-(w_1*x+w_0)))

x_range = np.linspace(-1, 500, 3000)

plt.figure(figsize=(9,5))
#plt.xkcd()
plt.legend(loc=2)


plt.plot(data1,np.zeros(len(data1)), 'o')
plt.plot(data1, model.predict_proba(data1), 'o')
plt.plot(x_range, sigmoid(x_range), '-')
​

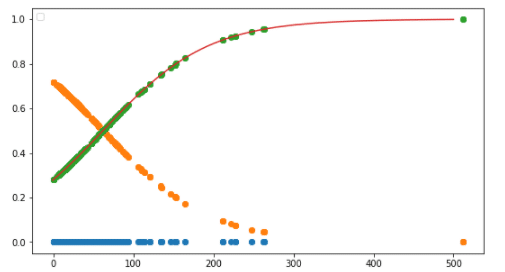
横が人数、縦が確率。緑が生存。オレンジが死亡として横300の場合90％以上生存していることがグラフからも分かる。そして、交点が60位で交わっていることも見て取れる。

【目的】：

特徴を増やして、もっと知ることが出来ないか確認。

【手段】：

カテゴリ変数の生成と、特徴量の生成で、2つの特徴を使って可視化してみる。

特徴量Genderの生成。男性女性をカテゴリ変数0，1に変換して格納。

titanic_df['Gender'] = titanic_df['Sex'].map({'female': 0, 'male': 1}).astype(int)

titanic_df['Pclass_Gender'] = titanic_df['Pclass'] + titanic_df['Gender']

Pclass_Genderと言う特徴量をPclassとGenderの合計から生成

titanic_df = titanic_df.drop(['Pclass', 'Sex', 'Gender','Age'], axis=1)

Pclass_Genderの材料の「Pclass', 'Sex', 'Gender」は不要。

Ageは保管された列がすでに欠損が埋められた列AgeFillが有るので不要。

np.random.seed = 0
xmin, xmax = -5, 85
ymin, ymax = 0.5, 4.5
index_survived = titanic_df[titanic_df["Survived"]==0].index
index_notsurvived = titanic_df[titanic_df["Survived"]==1].index
from matplotlib.colors import ListedColormap
fig, ax = plt.subplots()
cm = plt.cm.RdBu
cm_bright = ListedColormap(['#FF0000', '#0000FF'])
sc = ax.scatter(titanic_df.loc[index_survived, 'AgeFill'],
               titanic_df.loc[index_survived, 'Pclass_Gender']+(np.random.rand(len(index_survived))-0.5)*0.1,
               color='r', label='Not Survived', alpha=0.3)
sc = ax.scatter(titanic_df.loc[index_notsurvived, 'AgeFill'],
               titanic_df.loc[index_notsurvived, 'Pclass_Gender']+(np.random.rand(len(index_notsurvived))-0.5)*0.1,
               color='b', label='Survived', alpha=0.3)
ax.set_xlabel('AgeFill')
ax.set_ylabel('Pclass_Gender')
ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)
ax.legend(bbox_to_anchor=(1.4, 1.03))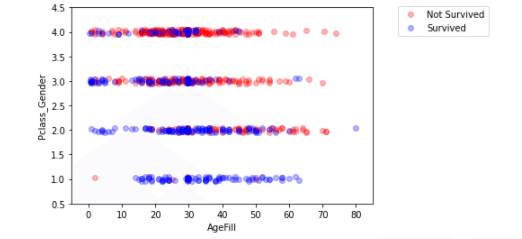

Pclass_Genderの数値が高く年齢も高い傾向にある人が死亡している傾向にありそう。と言う解釈が出来る。

更に境界線を引いてみる：手段：

data2 = titanic_df.loc[:, ["AgeFill", "Pclass_Gender"]].values
label2 =  titanic_df.loc[:,["Survived"]].values

説明変数と目的変数をdata2とlabel2格納。

model2 = LogisticRegression()

モデルを作って学習させる

model2.fit(data2, label2)

h = 0.02
xmin, xmax = -5, 85
ymin, ymax = 0.5, 4.5
xx, yy = np.meshgrid(np.arange(xmin, xmax, h), np.arange(ymin, ymax, h))
Z = model2.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]
Z = Z.reshape(xx.shape)
fig, ax = plt.subplots()
levels = np.linspace(0, 1.0)
cm = plt.cm.RdBu
cm_bright = ListedColormap(['#FF0000', '#0000FF'])
#contour = ax.contourf(xx, yy, Z, cmap=cm, levels=levels, alpha=0.5)
sc = ax.scatter(titanic_df.loc[index_survived, 'AgeFill'],
               titanic_df.loc[index_survived, 'Pclass_Gender']+(np.random.rand(len(index_survived))-0.5)*0.1,
               color='r', label='Not Survived', alpha=0.3)
sc = ax.scatter(titanic_df.loc[index_notsurvived, 'AgeFill'],
               titanic_df.loc[index_notsurvived, 'Pclass_Gender']+(np.random.rand(len(index_notsurvived))-0.5)*0.1,
               color='b', label='Survived', alpha=0.3)
ax.set_xlabel('AgeFill')
ax.set_ylabel('Pclass_Gender')
ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)
#fig.colorbar(contour)
x1 = xmin
x2 = xmax
y1 = -1*(model2.intercept_[0]+model2.coef_[0][0]*xmin)/model2.coef_[0][1]
y2 = -1*(model2.intercept_[0]+model2.coef_[0][0]*xmax)/model2.coef_[0][1]
ax.plot([x1, x2] ,[y1, y2], 'k--')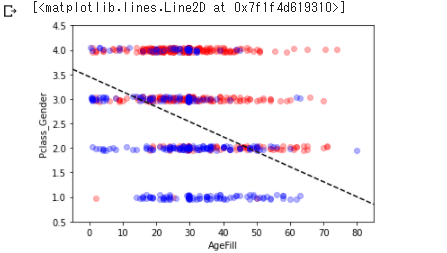

このグラフから年齢が60でPclass_Genderが2だと死亡してそう。

model2.predict([[60,2]])

死亡。

model2.predict_proba([[60,2]])

64％の確率で。これは、境界線からそれほど遠くに位置していないので、境界に近いので、ちょっとしたことで生き残る側に行く可能性があるという解釈も視覚的に容易である。

実際に学習させてみる：手段

混同行列とクロスバリデーション

#上記で作った特徴量が1個のデータ
traindata1, testdata1, trainlabel1, testlabel1 = train_test_split(data1, label1, test_size=0.2)
traindata1.shape
trainlabel1.shape

#上記で作った特徴量が二つ生成したデータ
traindata2, testdata2, trainlabel2, testlabel2 = train_test_split(data2, label2, test_size=0.2)
traindata2.shape
trainlabel2.shape

#特徴量が少し多めのデータ。ワンホットエンコーディング。
titanic_df["Embarked"]= pd.get_dummies(titanic_df["Embarked"], drop_first=True)

data = titanic_df.loc[:, ].values
label =  titanic_df.loc[:,["Survived"]].values
traindata, testdata, trainlabel, testlabel = train_test_split(data, label, test_size=0.2)
traindata.shape
trainlabel.shape

#ロジスティック回帰
eval_model1=LogisticRegression()
eval_model2=LogisticRegression()
eval_model=LogisticRegression()

print(eval_model1.score(traindata1, trainlabel1))
print(eval_model1.score(testdata1,testlabel1))

print(eval_model2.score(traindata2, trainlabel2))
print(eval_model2.score(testdata2,testlabel2))

特徴量が2つの方が学習出来ている事が分かる。

print(eval_model.score(traindata, trainlabel))
print(eval_model.score(testdata,testlabel))

from sklearn import metrics
print(metrics.classification_report(testlabel1, predictor_eval1))
print(metrics.classification_report(testlabel2, predictor_eval2))
print(metrics.classification_report(testlabel, predictor_eval))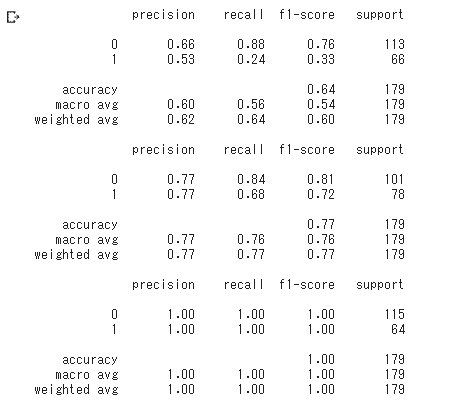

from sklearn.metrics import confusion_matrix
confusion_matrix1=confusion_matrix(testlabel1, predictor_eval1)
confusion_matrix2=confusion_matrix(testlabel2, predictor_eval2)
confusion_matrix=confusion_matrix(testlabel, predictor_eval)

#もう一回タイタニックデータ別のものを使ってみる
import seaborn as sns
sns.set(style="whitegrid")
# Load the example Titanic dataset
titanic = sns.load_dataset("titanic")
titanic.head()

#生死を縦軸に"class", "sex", "who", "alone"の関連性を見る。
# Set up a grid to plot survival probability against several variables
g = sns.PairGrid(titanic, y_vars="survived",
                x_vars=["class", "sex", "who", "alone"],
                size=5, aspect=.5)
# Draw a seaborn pointplot onto each Axes
g.map(sns.pointplot, color=sns.xkcd_rgb["plum"])
g.set(ylim=(0, 1))
sns.despine(fig=g.fig, left=True)
plt.show()

import seaborn as sns
sns.set(style="darkgrid")
# Load the example titanic dataset
df = sns.load_dataset("titanic")
# Make a custom palette with gendered colors
pal = dict(male="#6495ED", female="#F08080")
# Show the survival proability as a function of age and sex
g = sns.lmplot(x="age", y="survived", col="sex", hue="sex", data=df,
              palette=pal, y_jitter=.02, logistic=True)
g.set(xlim=(0, 80), ylim=(-.05, 1.05))
plt.show()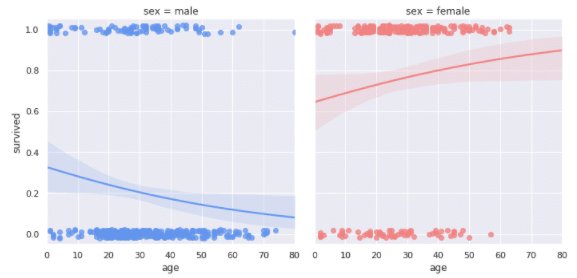

・主成分分析

高次元になるとデータが扱いにくく判断しにくい。その問題を解決するために主成分分析を利用する。

目的：高次元を分かりやすくする。ここでは2次元を1次元にしてみる。このことが出来れば4次元以上の次元を圧縮するイメージがつかめる。

手段：データから情報量が多い状態。分散が大きい状態を探すために、まずは分散を表現する。

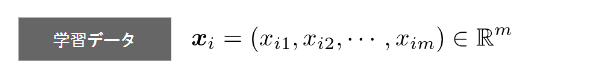
それぞれ、ｘｙデータがある。

ｘとｙの平均を出す。

それぞれのデータの平均との差を出すことが出来る。

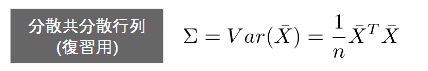
これで共分散分散行列を考えられる

一次元に圧縮する式。

この式から、最大に分散出来る式を考える。最大に分散＝情報が沢山ある。情報がたくさん残っているという考え方。

手段：制約をつけて値の限界を出す。

手段：本来のデータがどれだけ活かされているのか、損失しているのか判断して、次元削減がどれだけ精度を下げたかどれだけ活きているかを数値化する。

手段：ハンズオン、実際に数字をみて触ってみる。

from google.colab import drive
drive.mount('/content/drive')

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegressionCV
from sklearn.metrics import confusion_matrix
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
%matplotlib inline
cancer_df = pd.read_csv('/content/drive/My Drive/study_ai_ml/data/cancer.csv')

データの頭5行を見る

cancer_df.head()

一番最後が'Unnamed: 32'

cancer_df.drop('Unnamed: 32', axis=1, inplace=True)
cancer_df.head()

'Unnamed: 32'消す。

# 目的変数の抽出
y = cancer_df.diagnosis.apply(lambda d: 1 if d == 'M' else 0)

# 説明変数の抽出
X = cancer_df.loc[:, 'radius_mean':]

ちなみにｙは

# 学習用とテスト用でデータを分離
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# 標準化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# ロジスティック回帰で学習
logistic = LogisticRegressionCV(cv=10, random_state=0)
logistic.fit(X_train_scaled, y_train)
# 検証
print('Train score: {:.3f}'.format(logistic.score(X_train_scaled, y_train)))
print('Test score: {:.3f}'.format(logistic.score(X_test_scaled, y_test)))
print('Confustion matrix:\n{}'.format(confusion_matrix(y_true=y_test, y_pred=logistic.predict(X_test_scaled))))

Train score: 0.988
Test score: 0.972
Confustion matrix:
[[89 1]
[ 3 50]]

正解を正しく的中させた数が89。違うものを違うと的中させたのが50とかなり高精度になっている事がわかる。

pca = PCA(n_components=30)
pca.fit(X_train_scaled)
plt.bar([n for n in range(1, len(pca.explained_variance_ratio_)+1)], pca.explained_variance_ratio_)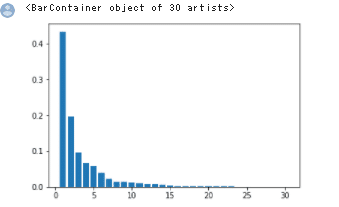

# PCA
# 次元数2まで圧縮
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_scaled)
print('X_train_pca shape: {}'.format(X_train_pca.shape))
# X_train_pca shape: (426, 2)
# 寄与率
print('explained variance ratio: {}'.format(pca.explained_variance_ratio_))
# explained variance ratio: [ 0.43315126  0.19586506]
# 散布図にプロット
temp = pd.DataFrame(X_train_pca)
temp['Outcome'] = y_train.values
b = temp[temp['Outcome'] == 0]
m = temp[temp['Outcome'] == 1]
plt.scatter(x=b[0], y=b[1], marker='o') # 良性は○でマーク
plt.scatter(x=m[0], y=m[1], marker='^') # 悪性は△でマーク
plt.xlabel('PC 1') # 第1主成分をx軸
plt.ylabel('PC 2') # 第2主成分をy軸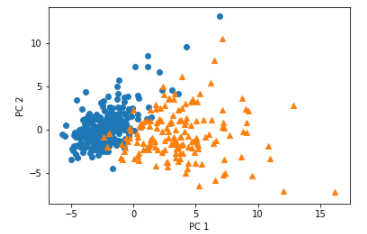

追記：関連レポート

import numpy as np
from matplotlib import pyplot as plt
from sklearn.datasets import load_iris

def pca_use_org(data):
   # ##################### 主成分分析 ########################
   # 共分散行列を求める
   cov_matrix = np.cov(data, rowvar=False)
   # 固有値と固有ベクトルを取得する
   l, v = np.linalg.eig(cov_matrix)
   # 固有値を大きい順に並べる
   l_index = np.argsort(l)[::-1]
   l_ = l[l_index]
   v_ = v[:, l_index]
   # 固有ベクトルを使ってデータを変換する
   data_trans = np.dot(data, v_)
   return data_trans, v_

if __name__ == "__main__":
   # ###################### データ作成 ########################
   # データセットから2次元データを切り出す
   d_index = [0, 2]
   iris = load_iris()
   data = iris.data
   data = data[:, d_index]
   # データ全体の平均を0にする
   print('data=', data)
   data -= data.mean(axis=0)
   print('data=', data)
   # #################### 主成分分析開始 #######################
   # 自作関数(numpyはその限りではない)でPCA
   data_trans, v = pca_use_org(data)
   # ###################### 作図準備 ###########################
   # 変換軸となるベクトルを描画用の変数に格納
   vec_s = [0, 0]
   vec_1st_e = [2*v[0, 0], 2*v[0, 1]]
   vec_2nd_e = [2*v[1, 0], 2*v[1, 1]]
   # ######################## 作図開始 ########################
   # -------------------- 変換前データと変換軸ベクトル ---------
   plt.figure(figsize=[8, 8])
   plt.xlim(-4, 4)
   plt.ylim(-4, 4)
   plt.quiver(vec_s[0], vec_s[1], vec_1st_e[0], vec_1st_e[1],
              angles='xy', scale_units='xy', scale=1, color='r', label='1st')
   plt.quiver(vec_s[0], vec_s[1], vec_2nd_e[0], vec_2nd_e[1],
              angles='xy', scale_units='xy', scale=1, color='b', label='2nd')
   plt.grid()
   plt.legend()
   plt.scatter(data[:, 0], data[:, 1], c=iris.target)
   plt.savefig('charts/fig-3.png')
   # -------------- 変換後データ、第1主成分、第2主成分 ---------
   plt.figure(figsize=[8, 8])
   plt.subplot2grid((4, 1), (0, 0), rowspan=2)
   plt.title('1st principal - 2nd principal')
   plt.grid()
   plt.scatter(data_trans[:, 0], data_trans[:, 1], c=iris.target)
   plt.subplot2grid((4, 1), (2, 0))
   plt.tick_params(labelleft="off", left="off")
   plt.title('1st principal')
   plt.grid()
   plt.scatter(data_trans[:, 0], np.zeros(len(data_trans[:, 0])), c=iris.target)
   plt.subplot2grid((4, 1), (3, 0))
   plt.title('2nd principal')
   plt.grid()
   plt.tick_params(labelleft="off", left="off")
   plt.scatter(data_trans[:, 1], np.zeros(len(data_trans[:, 1])), c=iris.target)
   plt.tight_layout()
   plt.show()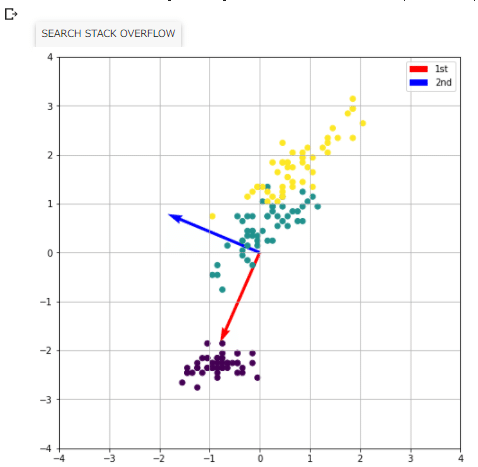

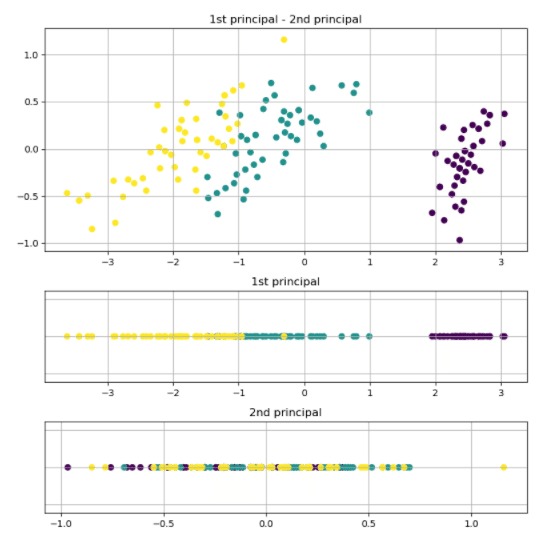
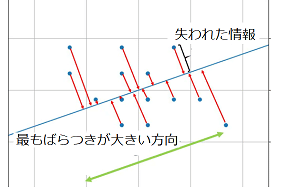
一次元に次元削減した角度から、データを確認すると一番分散が大きい方向で見ると情報量が多いことが分かる。

下の一次元は同じ大きさに見えるが、範囲を確認すると-1.0から1.0の間。比べて一番大きい方向を見ると-3から3までの範囲に情報が残っている。

・サポートベクトルマシン(SVM)

データの分類をする為の機械学習モデルの一種で、非常に強力なアルゴリズム。教師あり学習で、分類と回帰を扱うことができるが、主に分類のタスクで使われる。

2クラス分類問題とは「与えられた入力データが2つのカテゴリーのどちらに属するかを識別する問題」のこと。

もう少し数学的に表現する。与えられた入力データをxという数値ベクトルで表す。

※ベクトルは有効線分で表される（向きと大きさを意味する）

そしてこの入力データxが、AとBのどちらのカテゴリー(クラス)に属するかを表す変数をy。変数yは、入力データがAに分類される場合にはy= 1、Bに分類される場合にはy=1という値を取るとする。

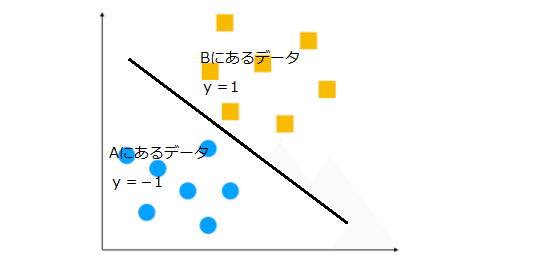
2クラス分類問題とは、何らかの特徴ベクトルxが与えられた時にラベルyの値を予想する問題、言い換えれば、xを与えた時にyの予測値を返す「関数」を構築する問題。※この場合-1とか1とかを返す関数。

特徴ベクトルxがどちらのクラスに属するか判定するため下記の関数が使われる。

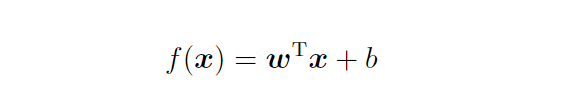
決定関数f(x)は、ベクトルxの入力に対してスカラーつまり、量（※方向は無い）。の値を返す関数となっている。式(1)においてwとbは事前には分からない未知のパラメータであり、これらをどのように推定するかが2クラス分類問題。このパラメータ推定の方法は多数考案され、SVMはその代表的な方法の1つ。

決定係数の分類のされ方。

変数yはラベル。sgnは符号関数と呼ばれる関数で、引数が正の場合には+1、負の場合には1を返す関数。

考え方として。特徴ベクトルxが2次元の場合。

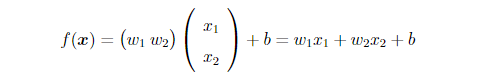
決定関数f(x)は図1に示すように平面を表す方程式

決定関数に含まれるパラメータw、bを適切に決定するためには、既にラベルの値が分かっている特徴ベクトルが複数必要。このような特徴ベクトルとラベルのセット(xi; yi)（iは 1;2;....; n番目）を訓練データ(training data)。以下では、SVMに基づいてこのn個の訓練データからパラメータw、bを決定する方法の解説。

ハードマージン

「n個の訓練データを全て正しく分類できるwとbの組が存在する」ということを数学的に仮定して表現する。全てのデータに対して、決定関数によるラベルの予測値sgnf(xi)と、訓練データyiの値(符号)が一致していることになるので、次式が成り立つ。

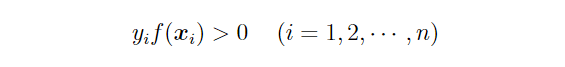
これは、ラベルｙiが例えば-1だった時、予測のｆ（ｘ）が-1という予測だったら掛け算してプラスになるね。

逆にラベルが+1で予測も+1だったら掛けたら1だから0以上と言う意味。

それを0以上にするということは全く間違わない。完全に分けた状態ということ。

2種類のデータの一番近い点で考えて、その2つが一番距離を取る状態を目指す。2点間はマージンと言う。点2つから出来た平行線をサポートベクトルと言い、平行に線が引かれる。サポートベクトルの真ん中に線を引く。それが分類境界線。

※点と平面の距離公式

ここでは訓練データが決定関数f(x)により分離可能なケースを考えているため、次のように変形する

ｙIは教師データの答えの部分-1か1か。

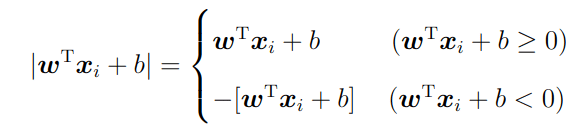
距離が線より上であれば、プラス×プラスで符号は+

線より下であればマイナス×マイナスで符号は+

純粋に量が表現できる。

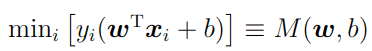
とする。M(W、ｂ)の最大化。下記はSVMの目的関数。

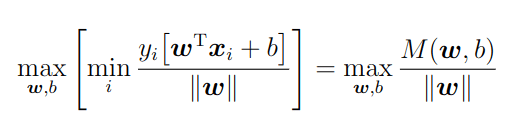
この最大化の条件から決定関数のパラメータwとbが決定。

M(w;b)　/　∥w∥を最大化したい場合には、M(w; b)がなるべく大きい方が良い。しかし、M(w; b)が大きくなりすぎると、条件を満たせない。超えてしまう。つまり、「yi[wTxi+b]≧M(w; b);条件を満たせる範囲で、最大化を行う」というのが、この目的関数の意味。一般にyi[wTxi+b]≧M(w; b);のような条件のことを制約条件(constrain)と言う。

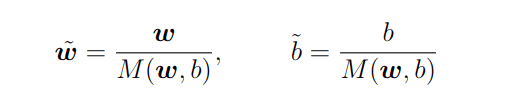
↑M(w; b)でw、bを規格化する。

これを扱いやすい形に変形する

係数は、後の計算を簡単にする目的でつけているだけで特に深い意味はない。この最適化問題が、分離可能性を仮定した場合の線形SV分類の標準的な定式化。なお、分離可能性を仮定したSV分類のことを一般にハードマージン(hard margin)。

SV分類ではマージン最大化、すなわち「分類境界f(x) = 0と分類境界から最も近くにあるデータxiとの距離の最大化」に基づいて分類境界が決定。

そのため、分類境界の決定に関わっているのは、分類境界に最も近いデータxiのみで、他のデータは関係ない。

実際、分類境界に最も近いデータ以外を取り除いてしまってもSV分類によって得られる分類境界は変化しない。

分類境界に最も近いデータxiが分類境界を支えていると解釈できるため、このxiのことをサポートベクトル(support vector)と言う。

ソフトマージン

ハードマージンは現実世界ではなかなか存在しない分類。なので、制約を緩和する。

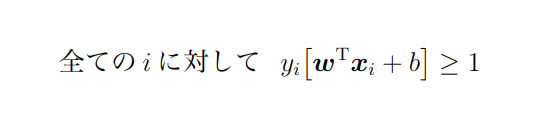
上記を緩和し、多少の分類誤りは許すようにすることで実現。このために新たに非負の変数

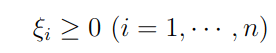
を導入し、上の制約条件を次のように変更。

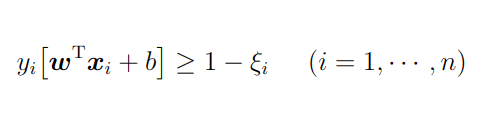
ξiはマージン内に入るデータや誤分類されたデータに対する誤差を表す変数となっており、スラック変数(slack variable)と呼ばれます。先ほどのハードマージンでは、マージンを分類境界とその分類境界に最も近いxi(サポートベクトル)との距離を用いて定義したが、ここでのソフトマージンでは↓

↑f(x) = 1とf(x) =1の間の距離をマージンを解釈する。

ハードマージン同様、このマージンを最大化しつつ、分類の誤差を最小化するように分類境界を決定する。

このソフトマージンの場合のSV分類における最適化問題は、数式的には次のように表現する。

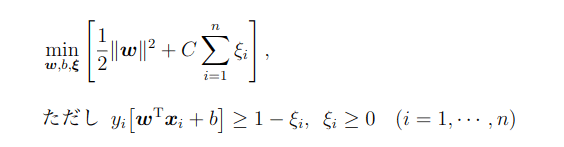
ただし、ξ= (ξ1....ξn)Tとしています。

係数Cは正則化係数(regularization parameter)と呼ばれる正の定数、学習前に値を与えておく必要があるハイパーパラメータ。目的関数の左はハードマージンの場合と同様にマージン最大化の働きを持つ。右は、本来の制約条件yi[wTxi+b]≧1からのズレを表すξiがなるべく小さくなるように抑制している。

この項によって、たとえマージンが大きくても誤分類がたくさん発生するような分類境界は作られにくくなっており、正則化係数Cがこの抑制の度合いを調整するパラメータ。

Cが大きいほどハードマージンの場合に近づく。C＝∞はハードマンジン

逆にCが小さいと誤分類しても目的関数への影響が少なくなるため、より誤分類が許容されやすくなります。つまり、Cが大きいほど誤分類が少なく良い分類境界を構成できますが、Cが大きすぎるとデータが分離可能でない場合、あらゆる分離境界に対して目的関数が発散して計算できなくなる可能性があります。そのため、実装する際にはデータに合わせてちょうど良いCの値を決定する必要があります。

Cを決める必要がある。方法は具体的にCの値の決定には、交差検証法(cross validation)などが用いる。

SVMにおける双対表現

の問題を最適化しないといけないということがわかった。

一般にこれらの最適化問題のことを、SV分類の主問題(primalproblem)と呼ぶ。

この主問題を解けば分類境界を決定できますが、SV分類ではこの主問題と等価な双対問題(dual problem)の方を解くことが一般的。

これは、SV分類における双対問題には主問題と比べて次のメリットがあるため。問題と比べて双対問題の方が変数を少なくできる分類境界の非線形化を考える上で双対問題の形式(双対形式)の方が有利となる。

以降は、双対問題を導出してしまい、その後で主問題と双対問題が今のSV分類の場合には等価な問題になっていることを説明する。

ラグランジュ(Lagrangue)関数と呼ばれる関数を導入

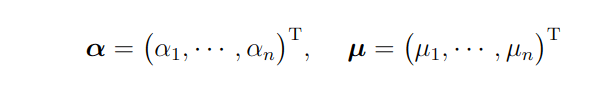
とする。

元々の最適化問題に登場する変数w,b,のことを主変数(primal variable)というのに対し、新たに導入した変数,のことを双対変数(dual variable)と呼びます27。双対問題とは、このラグランジュ関数

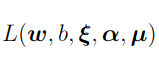
に関する次の最適化問題のこと。

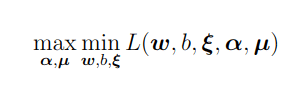
双対問題ではラグランジュ関数を主変数w,b,ξに関して最小化。極地問題の一端の各変数の偏微分の値が0を解く。

ラグランジュ関数の表式に代入して整理することで、簡潔に書き直す。

結果、αのみの関数になる。以上より、双対問題は次のように表現できることが分かる。

なお、ここまではソフトマージンの場合の双対問題を考えたが、C!1とすることでハードマージンの場合の双対問題も

SV分類において双対問題を考えるメリットとして変数が減らせる、変数が減って解くのが簡単。。。

主問題と双対問題の関係

上記の双対問題が、SV分類の場合には主問題と等価になっていることを説明。この主問題と双対問題の関係を理解するためには、次の2つのステップを踏む必要がある。

ラグランジュ関数の双対変数,α、μに関する最大化に関して、下記の様に計算

Step1を考える

の部分を考える。もし、全てのiに対して

全てのiに対して式(53)、(54)が成り立つ時のみ考えることができて、その場合には、

ソフトマージンの場合の主問題ということが言える。

Step2を考える

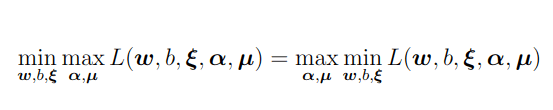
この問題は

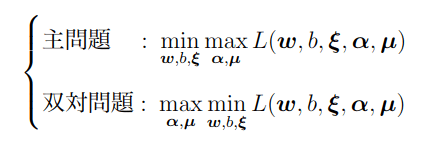
どちらも最大化maxと最小化minが2つ付いているが、ここまで見てきたように結局のところ、主問題は主変数(w; b;ξ)、双対問題は双対変数(α;μ)に関する最適化問題。

それぞれの最適化問題の最適解を

とした時、

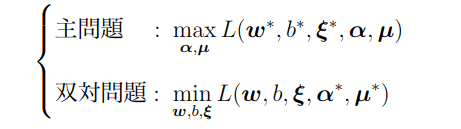
この不等式が成り立つ。主問題と双対問題の最適値に関しては、次の不等式が成り立つ。

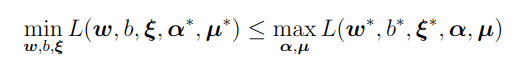
これは「双対問題の最適値は主問題の最適値以下となる」ということを意味し、この主問題と双対問題の最適値に関する性質は、弱双対性(weak duality)と言う。

この性質は、SV分類に限らずあらゆる最適化問題で成立する。ただし、SV分類の場合には、これよりさらに強い以下の強双対性(strong duality)と呼ばれる性質が成り立つことが分かっている。

この式は、主問題と双対問題の目的関数値が最適解において一致することを意味し、この強双対性が成り立つ場合に、

主変数(w; b;ξ)に関して極小点、双対変数(α; μ)に関しては極大点であることを意味している。ラグランジュ関数鞍点ということでも有る。

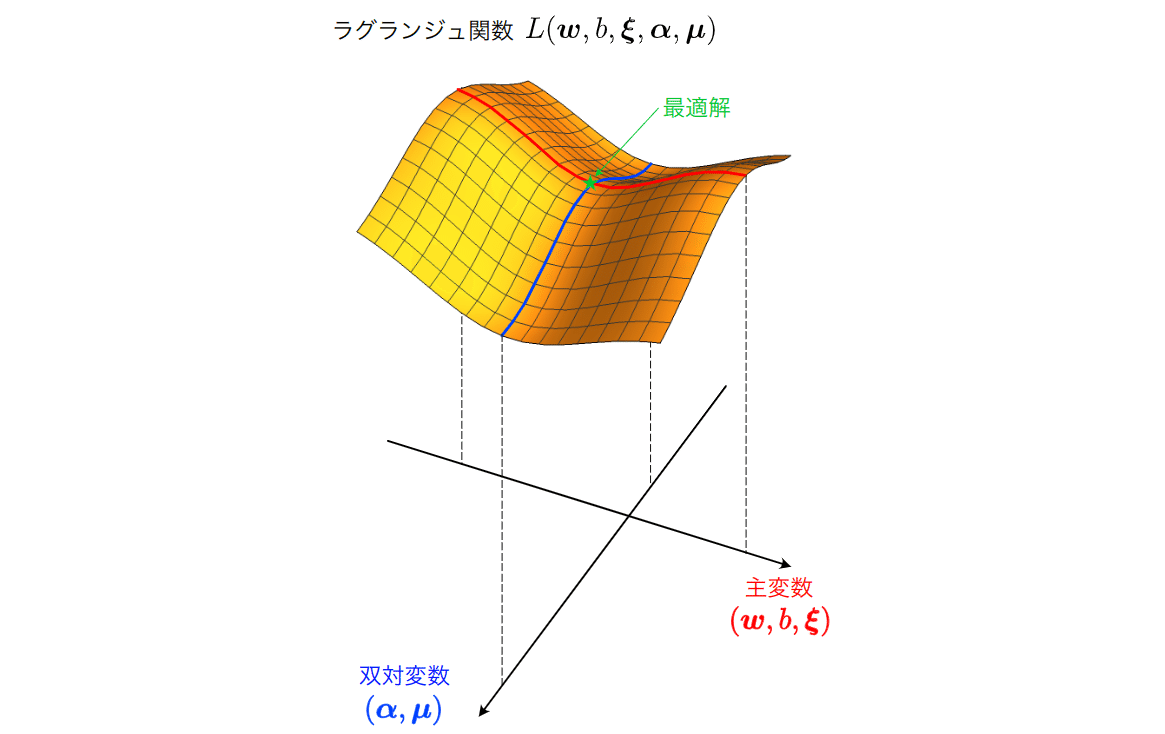
結果：主問題を解いても双対問題を解いても結局は同じ最適化が得られる。

カーネルを用いた非線形分離への拡張

3次元で考える。

高次元データへの拡張は、数学的には写像(map)と呼ばれます。上の例では下記の写像を考えた。

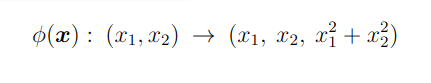
高次元データへ写像する関数をφ(x)とし、これを一般化すれば、入力空間でn次元であるデータをより高次のr次元の特徴空間へ変換する関数は

しかし計算量が莫大になるため、φの内積部分をカーネル関数(kernel function)と呼ばれる関数で置き換える。

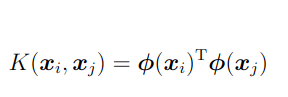
双対問題をカーネル関数を用いて表現する

また、決定関数f(x)もカーネル関数を用いて

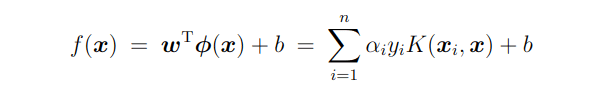
代表的な関数形は、次の3つある。

関数に含まれるc,d,γといったパラメータはハイパーパラメータで事前に決定しておく必要があります。また、ガウスカーネルのことはRBF (radial basis function)カーネルと呼ぶこともあります。詳細は省略しますが、データに合わせて適切なカーネルを選んで計算を行うことで、SVMを用いた入力データの非線形分離が可能となります。

SNMハンズオン

【線形分離可能】

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

def gen_data():
   x0 = np.random.normal(size=50).reshape(-1, 2) - 2.
   x1 = np.random.normal(size=50).reshape(-1, 2) + 2.
   X_train = np.concatenate([x0, x1])
   ys_train = np.concatenate([np.zeros(25), np.ones(25)]).astype(np.int)
   return X_train, ys_train

X_train, ys_train = gen_data()
plt.scatter(X_train[:, 0], X_train[:, 1], c=ys_train)

t = np.where(ys_train == 1.0, 1.0, -1.0)

n_samples = len(X_train)
# 線形カーネル
K = X_train.dot(X_train.T)

eta1 = 0.01
eta2 = 0.001
n_iter = 500

H = np.outer(t, t) * K

a = np.ones(n_samples)
for _ in range(n_iter):
   grad = 1 - H.dot(a)
   a += eta1 * grad
   a -= eta2 * a.dot(t) * t
   a = np.where(a > 0, a, 0)

index = a > 1e-6
support_vectors = X_train[index]
support_vector_t = t[index]
support_vector_a = a[index]

term2 = K[index][:, index].dot(support_vector_a * support_vector_t)
b = (support_vector_t - term2).mean()
xx0, xx1 = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
xx = np.array([xx0, xx1]).reshape(2, -1).T

X_test = xx
y_project = np.ones(len(X_test)) * b
for i in range(len(X_test)):
   for a, sv_t, sv in zip(support_vector_a, support_vector_t, support_vectors):
       y_project[i] += a * sv_t * sv.dot(X_test[i])
y_pred = np.sign(y_project)
# 訓練データを可視化
plt.scatter(X_train[:, 0], X_train[:, 1], c=ys_train)
# サポートベクトルを可視化
plt.scatter(support_vectors[:, 0], support_vectors[:, 1],
                   s=100, facecolors='none', edgecolors='k')
# 領域を可視化
plt.contourf(xx0, xx1, y_pred.reshape(100, 100), alpha=0.2, levels=np.linspace(0, 1, 3))
# マージンと決定境界を可視化
plt.contour(xx0, xx1, y_project.reshape(100, 100), colors='k',
                    levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])


# マージンと決定境界を可視化
plt.quiver(0, 0, 0.1, 0.35, width=0.01, scale=1, color='pink')​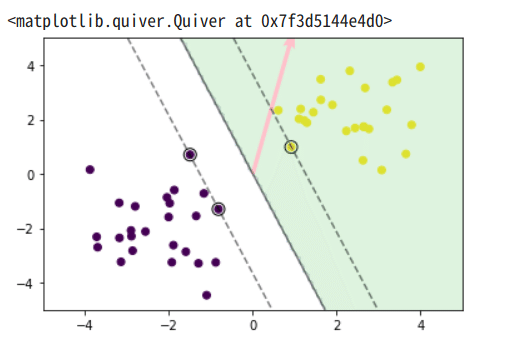

サポートベクトルが3つ確認。

【線形分離不可能】

factor = .2
n_samples = 50
linspace = np.linspace(0, 2 * np.pi, n_samples // 2 + 1)[:-1]
outer_circ_x = np.cos(linspace)
outer_circ_y = np.sin(linspace)
inner_circ_x = outer_circ_x * factor
inner_circ_y = outer_circ_y * factor
X = np.vstack((np.append(outer_circ_x, inner_circ_x),
              np.append(outer_circ_y, inner_circ_y))).T
y = np.hstack([np.zeros(n_samples // 2, dtype=np.intp),
              np.ones(n_samples // 2, dtype=np.intp)])
X += np.random.normal(scale=0.15, size=X.shape)
x_train = X
y_train = y

plt.scatter(x_train[:,0], x_train[:,1], c=y_train)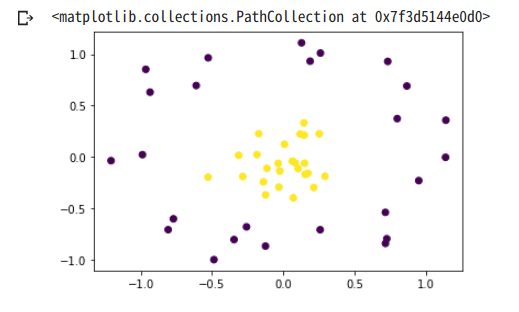

元のデータ空間では線形分離は出来ないが、特徴空間上で線形分離することを考える。

今回はカーネルとしてRBFカーネル

def rbf(u, v):
       sigma = 0.8
       return np.exp(-0.5 * ((u - v)**2).sum() / sigma**2)
   
X_train = x_train
t = np.where(y_train == 1.0, 1.0, -1.0)
n_samples = len(X_train)
# RBFカーネル
K = np.zeros((n_samples, n_samples))
for i in range(n_samples):
   for j in range(n_samples):
       K[i, j] = rbf(X_train[i], X_train[j])
eta1 = 0.01
eta2 = 0.001
n_iter = 5000
H = np.outer(t, t) * K
a = np.ones(n_samples)
for _ in range(n_iter):
   grad = 1 - H.dot(a)
   a += eta1 * grad
   a -= eta2 * a.dot(t) * t
   a = np.where(a > 0, a, 0)

index = a > 1e-6
support_vectors = X_train[index]
support_vector_t = t[index]
support_vector_a = a[index]
term2 = K[index][:, index].dot(support_vector_a * support_vector_t)
b = (support_vector_t - term2).mean()

xx0, xx1 = np.meshgrid(np.linspace(-1.5, 1.5, 100), np.linspace(-1.5, 1.5, 100))
xx = np.array([xx0, xx1]).reshape(2, -1).T
X_test = xx
y_project = np.ones(len(X_test)) * b
for i in range(len(X_test)):
   for a, sv_t, sv in zip(support_vector_a, support_vector_t, support_vectors):
       y_project[i] += a * sv_t * rbf(X_test[i], sv)
y_pred = np.sign(y_project)

# 訓練データを可視化
plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train)
# サポートベクトルを可視化
plt.scatter(support_vectors[:, 0], support_vectors[:, 1],
                   s=100, facecolors='none', edgecolors='k')
# 領域を可視化
plt.contourf(xx0, xx1, y_pred.reshape(100, 100), alpha=0.2, levels=np.linspace(0, 1, 3))
# マージンと決定境界を可視化
plt.contour(xx0, xx1, y_project.reshape(100, 100), colors='k',
                    levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])
      

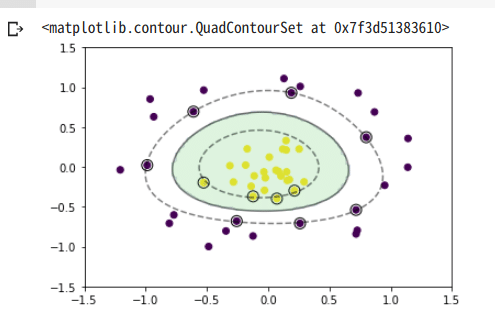
ソフトマージンSVM

x0 = np.random.normal(size=50).reshape(-1, 2) - 1.
x1 = np.random.normal(size=50).reshape(-1, 2) + 1.
x_train = np.concatenate([x0, x1])
y_train = np.concatenate([np.zeros(25), np.ones(25)]).astype(np.int)

plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train)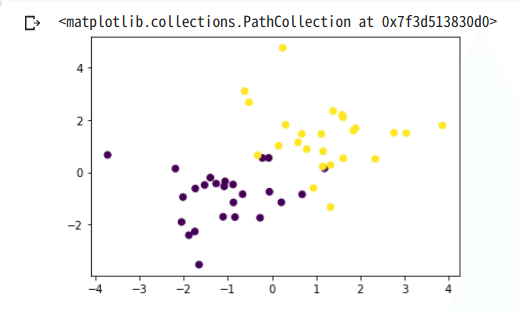

X_train = x_train
t = np.where(y_train == 1.0, 1.0, -1.0)
n_samples = len(X_train)
# 線形カーネル
K = X_train.dot(X_train.T)
C = 1
eta1 = 0.01
eta2 = 0.001
n_iter = 1000
H = np.outer(t, t) * K
a = np.ones(n_samples)
for _ in range(n_iter):
   grad = 1 - H.dot(a)
   a += eta1 * grad
   a -= eta2 * a.dot(t) * t
   a = np.clip(a, 0, C)

index = a > 1e-8
support_vectors = X_train[index]
support_vector_t = t[index]
support_vector_a = a[index]
term2 = K[index][:, index].dot(support_vector_a * support_vector_t)
b = (support_vector_t - term2).mean()

xx0, xx1 = np.meshgrid(np.linspace(-4, 4, 100), np.linspace(-4, 4, 100))
xx = np.array([xx0, xx1]).reshape(2, -1).T
X_test = xx
y_project = np.ones(len(X_test)) * b
for i in range(len(X_test)):
   for a, sv_t, sv in zip(support_vector_a, support_vector_t, support_vectors):
       y_project[i] += a * sv_t * sv.dot(X_test[i])
y_pred = np.sign(y_project)

# 訓練データを可視化
plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train)
# サポートベクトルを可視化
plt.scatter(support_vectors[:, 0], support_vectors[:, 1],
                   s=100, facecolors='none', edgecolors='k')
# 領域を可視化
plt.contourf(xx0, xx1, y_pred.reshape(100, 100), alpha=0.2, levels=np.linspace(0, 1, 3))
# マージンと決定境界を可視化
plt.contour(xx0, xx1, y_project.reshape(100, 100), colors='k',
                    levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])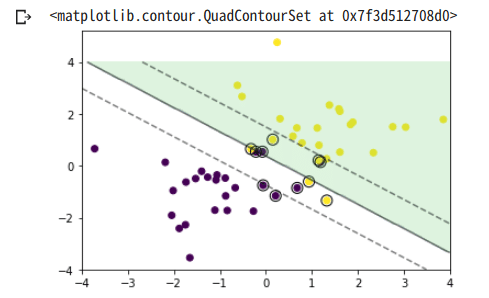

追記：関連レポート

scikit-learnでのSVM

import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
iris = load_iris()
dataset = pd.DataFrame(data = iris['data'], columns = iris['feature_names'])
dataset['species'] = iris['target']
dataset.head()

Y = np.array(dataset['species'])
X = np.array(dataset[iris['feature_names']])
# データの分割
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=0)

from sklearn.svm import SVC
model = SVC(gamma='scale')
model.fit(X_train, Y_train)

学習してモデル構築

Y_pred = model.predict(X_test)
print(Y_test[:10])
print(Y_pred[:10])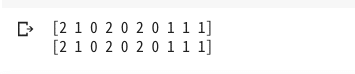

10項目の身の出力では有るが精度の高い結果が得られている。